1. What This Chapter is About
2. NONMEM Describes its Inputs
3. PREDPP Describes Its Inputs
4. Diagnostic Output from the Estimation Step
4.1. Intermediate Output from the Estimation Step
4.2. Summary Output from the Estimation Step
5. Final Parameter Estimates
6. Output from the Covariance Step
7. Additional Output: Tables and Scatterplots
7.1. Output from the Table Step
7.2. Output from the Scatterplot Step
NONMEM Users Guide Part V - Introductory Guide
- Chapter 10
Chapter 10 - Reading the Output
1. What This Chapter is About
This chapter describes NONMEM’s output in
detail. Each page of a NONMEM-PREDPP output file is shown
and discussed.
The input file to NM-TRAN is that of figure 2.12,
which is reproduced here as figure 10.1 for
convenience.
Figure 10.1. The NM-TRAN input file (same as figure 2.12). The line numbers on the left are not actually part of the file.
2. NONMEM Describes its Inputs
The first page of NONMEM’s output is shown
in figure 10.2. In this page, NONMEM repeats
("echos") the instructions it was given in the
control file and describes the data file. The first page of
the output should be checked carefully. Problems in a NONMEM
run can often be traced to errors in the problem
specification. For example, always check that the initial
parameter estimates were entered correctly.
Figure 10.2. The first page of the output report. The line numbers on the left are not actually part of the report.
Line 5 is an identification line for the output
report. The contents of the $PROBLEM record are shown
here.
Line 7 indicates that this is not a data checkout
run. (Data checkout mode is discussed in Chapter 12 Section
4.10.) Lines 8 through 27 describe the input data file.
Lines 10 and 11 describe the numbers of rows and columns in
the input file, as shown in figure 6.1. Specifically, line
10 shows how many data records were read according to the
FORTRAN format specification given in line 24. Line 11
describes the number of data items per record, which is the
number of data items listed in the $INPUT record, less any
that were dropped by the Data Preprocessor, plus any that it
added (see Chapter 6). Lines 12, 13, and 14 describe the
locations of those data items of interest to NONMEM itself
(i.e. NONMEM data items). Lines 16 through 18 are discussed
in Section 3. Line 21 gives the labels for all the data
items. The first six labels are those of the data items
specified in the $INPUT record and the next two (EVID, MDV)
are those of two data items added to the data set by the
Data Preprocessor. (NONMEM itself supplies labels PRED, RES,
and WRES for the prediction, residual, and weighted residual
data items.) In the terminology of Chapter 4 (e.g. (4.15a)),
ID, TIME, AMT, WT, and APGR are the elements of
 ; DV is
; DV is
 ; PRED is
; PRED is
 (evaluated for the typical
individual in the population). Line 24 shows the format used
to read each data record. In this example, the format was
generated by the Data Preprocessor and describes the data
file after processing by the Data Preprocessor.†
----------
(evaluated for the typical
individual in the population). Line 24 shows the format used
to read each data record. In this example, the format was
generated by the Data Preprocessor and describes the data
file after processing by the Data Preprocessor.†
----------

Line 26 gives the number of observation records.
Line 27 gives the number of individual records; that is, one
less than the number of times that the ID data item changed
value.
Lines 29 through 47 describe the contents of the
$THETA, $OMEGA and $SIGMA records. First, the number of
elements of  ,
,
 and
and
 are given (lines 29, 31 and
33), then their initial estimates are displayed. In lines
38-41, notice the values 0.1000e+07 and -0.1000e+07. These
are NONMEM’s way of expressing the values
are given (lines 29, 31 and
33), then their initial estimates are displayed. In lines
38-41, notice the values 0.1000e+07 and -0.1000e+07. These
are NONMEM’s way of expressing the values
 and
and
 ; i.e., of describing
; i.e., of describing
 s which are unbounded on
one or both sides. Another FORTRAN system may display these
numbers differently (e.g., 1.0000e+06), but the absolute
value will always be 1,000,000. In lines 43 and 44, notice
that the variances from the $OMEGA record appear along the
diagonal of the
s which are unbounded on
one or both sides. Another FORTRAN system may display these
numbers differently (e.g., 1.0000e+06), but the absolute
value will always be 1,000,000. In lines 43 and 44, notice
that the variances from the $OMEGA record appear along the
diagonal of the  matrix, and
that the off-diagonal element
matrix, and
that the off-diagonal element
 is zero. Line 31 states
that NONMEM understands
is zero. Line 31 states
that NONMEM understands  to
be diagonal; the off-diagonal element(s) are automatically
fixed at zero.
to
be diagonal; the off-diagonal element(s) are automatically
fixed at zero.
The remaining lines of figure 10.2 describe the
tasks that NONMEM will perform. Lines 49 through 53 describe
the $ESTIMATION record. Lines 50 through 53 show the
defaults (set by NM-TRAN) for various options, all of which
could have been specified explicitly on the $ESTIMATION
record. In line 50 for example, NONMEM displays the maximum
number of times it will evaluate the objective function
during the Estimation Step (this number can be slightly
exceeded). The value 360 was supplied by NM-TRAN. It is a
function of the sizes of  ,
,
 , and
, and
 . Line 51 displays the
desired number of significant digits in the final parameter
estimate; the value 3 is the default number requested by
NM-TRAN.
. Line 51 displays the
desired number of significant digits in the final parameter
estimate; the value 3 is the default number requested by
NM-TRAN.
Lines 55 through 59 describe the $COVARIANCE
record, giving the default options chosen by
NM-TRAN.
Lines 59 through 61 describe the $TABLE record.
Lines 67 through 73 describe the $SCATTERPLOT
records.
3. PREDPP Describes Its Inputs
The next two pages are produced by PREDPP and
will not appear if $PRED statements (or a user-written PRED
subroutine) are used. PREDPP uses these pages to repeat
("echo") the instructions it was given in the
control file, and to identify the ADVAN and TRANS routines
chosen by the user. The first page of PREDPP’s output
is shown in figure 10.3.
Figure 10.3. The first page of PREDPP's output. The line numbers on the left are not actually part of the report.
In its first page of output, PREDPP describes the
features of the pharmacokinetic model and its
parameterization encoded into the ADVAN and TRANS routines
specified on the $SUBROUTINE record. The information
displayed here includes the kind of information summarized
in Appendices 1 and 2. In the particular output of Figure
10.3 no information concerning an alternate parameterization
appears because TRANS1 was specified. The information
concerning basic parameters and compartments is displayed in
a format similar to that used in NONMEM Users Guide, Part
VI, which is the complete reference for PREDPP.
Lines 5 and 8 describe the basic PK parameters,
which in this example is the single microconstant K. If a
translator other than TRANS1 had been requested, an
additional line would appear describing the translation.
E.g., with TRANS2, this line would read:
TRANSLATOR WILL CONVERT PARAMETERS CLEARANCE (CL)
AND VOLUME (V) to K
Lines 10 through 14 describe the compartment
attributes. Even though the output compartment is never
turned on by the data of this example, its attributes are
described here because it is part of the model.
The information presented so far describes the
model for computing drug amounts. For a given choice of
ADVAN and TRANS, the contents of this page are completely
fixed. PREDPP’s second page of output describes user
choices related to the given ADVAN routine, including
choices for the scale parameters (and thus, to the model for
computing concentrations). This page is shown in figure
10.4.
Figure 10.4. The second page of PREDPP's output. The line numbers on the left are not actually part of the report.
Lines 2 through 9 describe the additional PK
parameters that are computed by the $PK statements (or PK
subroutine). In line 5, the position marked with
"3" corresponds to the scale parameter for
compartment number 1. Thus, we know that the $PK statements
contained an assignment statement for S1. From the prior
page we can see that compartment number 1 is the central
compartment. The value "3" is a row number within
GG, an array used for communication between PREDPP and the
PK subroutine. With the use of NM-TRAN and $PK statements,
row numbers are of no interest to the user. With a
user-written PK subroutine, it is important to check their
correctness. Positions marked with "*" correspond
to additional PK parameters that are allowed by the model
but that are not assigned a value by $PK statements; an
example is F1, the bioavailability fraction for compartment
1. Positions marked with "-" correspond to
additional parameters that may not be computed; for
instance, dose-related parameters are not allowed for the
output compartment, because (as shown on the preceding page)
this compartment cannot receive doses.
Lines 11 through 14 describe the locations in the
input data record of those data items of interest to PREDPP
(PREDPP data items). (NM-TRAN causes the locations of these
data items in the data set to be passed by NONMEM to PREDPP,
as indicated in lines 15 through 17 of figure 10.2. NONMEM
is not concerned with the significance of these data items.)
Note that data item 7, Event ID, was appended by the Data
Preprocessor.
Line 17 reflects the fact that, by default, $PK
statements are evaluated with every event record†.
Lagged and additional doses are discussed in Chapter 12,
Sections 2.4 and 2.5. They are not used in this example.
----------

Line 21 reflects the fact that the $ERROR
statements describe the simple error model (3.4). This model
uses no data items and no elements of
 whatsoever (directly or
indirectly). NM-TRAN has instructed PREDPP that the $ERROR
statements need be evaluated only once at the beginning of
the problem. Line 20 indicates that, should the Simulation
Step be implemented, PREDPP will disregard this limitation
and evaluate the $ERROR statements with every event record,
so that randomly-generated values of intra-individual error
can be applied at every observation event. (This example
does not involve simulation, but the PK and ERROR routines
which implement the $PK and $ERROR statements are capable of
supporting all NONMEM tasks, including
simulation.)
whatsoever (directly or
indirectly). NM-TRAN has instructed PREDPP that the $ERROR
statements need be evaluated only once at the beginning of
the problem. Line 20 indicates that, should the Simulation
Step be implemented, PREDPP will disregard this limitation
and evaluate the $ERROR statements with every event record,
so that randomly-generated values of intra-individual error
can be applied at every observation event. (This example
does not involve simulation, but the PK and ERROR routines
which implement the $PK and $ERROR statements are capable of
supporting all NONMEM tasks, including
simulation.)
Finally, note that the $PK and $ERROR models
(figure 10.1, lines 5-14) are not documented in the
NONMEM-PREDPP output. It is a good idea to attach a printed
copy of the NM-TRAN input records to the corresponding
NONMEM output.
4. Diagnostic Output from the Estimation Step
The next page of output, figure 10.5, is produced
during the running of the Estimation Step.
Figure 10.5. The output from the Estimation Step. The line numbers on the left are not actually part of the report.
4.1. Intermediate Output from the Estimation Step
Lines 1 through 42 are referred to as the
intermediate output. Lines 4 through 7 give numbers
summarizing the 0-th iteration, which are based on the
initial parameter estimates. Line 4 shows the initial value
of the objective function. The value following "NO. OF
FUNC. EVALS." is the number of objective function
evaluations which were needed during the iteration. Line 5
gives the cumulative number of function evaluations
including this and all prior iteration summaries. Line 6
gives the scaled transformed parameter estimates. Each
parameter being estimated is first transformed to an
unconstrained parameter  ,
and then divided by
,
and then divided by 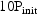 (scaled), where
(scaled), where 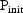 is the
transformed initial estimate of the parameter. The result of
this two-stage conversion is a new parameter called the
scaled transformed parameter (STP). Thus, in line 6,
all parameters are .1 at the 0-th iteration. Parameters are
printed in the following order: elements of
is the
transformed initial estimate of the parameter. The result of
this two-stage conversion is a new parameter called the
scaled transformed parameter (STP). Thus, in line 6,
all parameters are .1 at the 0-th iteration. Parameters are
printed in the following order: elements of
 , elements of
, elements of
 , elements of
, elements of
 . In this example, reading
from left to right, the parameters are
. In this example, reading
from left to right, the parameters are
 ,
,
 ,
,
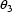 ,
,
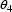 ,
,
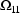 ,
,
 , and
, and
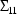 .
.
Two points should be noted. First, fixed
parameters do not appear in the list. Therefore, the
off-diagonal element  ,
which is effectively fixed to 0, does not appear. Second,
when off-diagonal elements of
,
which is effectively fixed to 0, does not appear. Second,
when off-diagonal elements of
 are being estimated, then
as many additional STP’s appear as there are
off-diagonal elements of
are being estimated, then
as many additional STP’s appear as there are
off-diagonal elements of  being estimated. However, a 1-1 correspondence between each
of the elements of
being estimated. However, a 1-1 correspondence between each
of the elements of  and an
STP does not exist. The same is true for elements of
and an
STP does not exist. The same is true for elements of
 and the STP’s for
and the STP’s for
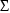 when off-diagonal elements
of
when off-diagonal elements
of 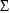 are
estimated.
are
estimated.
Line 7 shows the gradient for each parameter,
which may be thought of as the partial derivative of the
objective function with respect to that
parameter.
The Estimation Step proceeds in a series of
stages called iterations. In this example, intermediate
printout is produced for each of every 5 iterations, as well
as for the 0-th and final iterations, for which intermediate
printout is always printed by default. This printout
consists of the same four lines as for the 0-th iteration,
but using the parameters estimates obtained at the end of
the iteration.
In lines 4, 9, 14, 19, 24, 29, 34, and 39,
observe that the objective function drops quickly at first,
and then more slowly. After iteration number 25, there is no
change above the fourth significant digit.
In lines 6, 11, 16, 21, 26, 31, 36, and 41,
observe that each parameter also changes rapidly at first
and then more slowly as it converges to its final value.
(The first parameter,  , is
an exception. It is clearly approaching a very small value
close to its lower bound, 0. In Chapter 12, we shall see
that both
, is
an exception. It is clearly approaching a very small value
close to its lower bound, 0. In Chapter 12, we shall see
that both 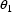 and
and
 are best fixed at
0.)
are best fixed at
0.)
Finally, in lines 7, 12, 17, 22, 27, 32, 37, and
42, observe that the gradients also approach 0, another sign
that a minimum of the objective function has been
located.
The values computed for the gradients are very
sensitive to differences in computer arithmetic and
precision. If a given NONMEM run is repeated on a different
computer, or on the same computer with different machine
precision or a different FORTRAN compiler, it is likely that
the gradients will be different. This will cause the search
to follow a different path to the minimum, so that lines 4
through 42 may be quite different. However, each final
estimate of a STP should always be the same to the number of
requested significant digits. (Minor differences may also be
observed in the output of the Covariance Step, below; this
output is also sensitive to computational
differences.)
4.2. Summary Output from the Estimation Step
Lines 44, 45 and 46 are always printed, even when
intermediate printout is suppressed. Line 44,
"MINIMIZATION SUCCESSFUL", signifies that the
search appears to have located a minimum of the objective
function. Before one can be certain that a minimum has been
located, or one which corresponds to a reasonable parameter
estimate (there can be a number of "local
minima"), the final parameter estimates must be
examined in their (unscaled untransformed) state; see
Section 5 below. The Estimation Step is not always
successful. Chapter 13 discusses two other messages that
sometimes appear instead of line 44.
In line 45, note that the number of function
evaluations used, 315, is a total value and includes all
iterations (not just those for which intermediate printout
was displayed). This is under the limit of 360 supplied by
NM-TRAN (figure 10.2, line 50).
The number of significant digits in the final
estimate is given in line 34 as 3.9. This can be interpreted
as meaning that no (scaled transformed) parameter
estimate is actually determined to less than 3.9
significant digits. More specifically, when the STP
estimates were compared between the last two iterations,
none differed in the first (almost) 4 significant figures
including leading zeros after the decimal point. Note
that the final 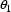 STP estimate
is .949e-10, and so the 949 are not significant digits at
all! Because NONMEM displays only 3 significant digits in
the printed parameter estimates, and for other reasons as
well, by default NM-TRAN requests only 3 significant digits.
However, more significance can be requested, as was
discussed in Chapter 9, Section 4.1.
STP estimate
is .949e-10, and so the 949 are not significant digits at
all! Because NONMEM displays only 3 significant digits in
the printed parameter estimates, and for other reasons as
well, by default NM-TRAN requests only 3 significant digits.
However, more significance can be requested, as was
discussed in Chapter 9, Section 4.1.
5. Final Parameter Estimates
The next two pages in the NONMEM output are
produced whether or not the Estimation Step was implemented
and, if it was, whether or not the search terminated
successfully. They give the values of the objective function
and the parameter estimates, using the final parameter
estimates if the Estimation Step was implemented (whether or
not the search terminated successfully), and using the
initial parameter estimates otherwise. These pages have
already been shown in Chapter 2, figure 2.13. Even when the
minimization routine is successful in locating a minimum of
the objective function, the final (unscaled untransformed)
parameter estimates must be carefully checked. Is any
parameter’s final estimate physiologically
unreasonable? Is any parameter’s final estimate near
its upper or lower constraint? If either answer is yes, the
model, the constraints on  ’s, or the data may be incorrect; see Chapter
11.
’s, or the data may be incorrect; see Chapter
11.
Sometimes the final estimates do not match
anticipated values, e.g., values obtained by some other
system of analysis. Additional refinement of the model may
be needed, as discussed in Chapter 11. However, the
discrepancy may well be traceable to an error in model
specification, such as an error in specifying a
compartment’s scale. Along with the Estimation Step,
it is important to obtain a scatterplot of PRED vs DV and
make sure the unit slope line is visible. See Chapter 13,
Section 4.4.
6. Output from the Covariance Step
Figures 10.6 through 10.7 show the output of the
Covariance Step, which was requested via the $COVARIANCE
record. Figure 10.6 has already been displayed as figure
2.14, but is included here for completeness. This page
displays the standard errors of the parameter estimates.
Standard errors are discussed extensively in Chapters 5 and
11. A detailed discussion of the remaining three pages,
containing the covariance, correlation, and inverse
covariance matrices, is beyond the scope of this text. Note,
however, the use of the notation "........". Each
sequence of dots denotes a value (such as the standard error
in the estimate of 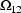 ) that
is 0 by definition, rather than due to a
computation.
) that
is 0 by definition, rather than due to a
computation.
Figure 10.6. Standard error of the estimate. The line numbers on the left are not actually part of the report.
Figure 10.7. Covariance matrix of the estimate. The line numbers on the left are not actually part of the report.
Figure 10.8. Correlation matrix of the estimate. The line numbers on the left are not actually part of the report.
Figure 10.9. Inverse covariance matrix of the estimate. The line numbers on the left are not actually part of the report.
7. Additional Output: Tables and Scatterplots
The use of $TABLE and $SCATTERPLOT records to
request tables and scatterplots is discussed in Chapter
9.
7.1. Output from the Table Step
The first 12 lines of the table produced by the
$TABLE record are shown in figure 10.10. This is the data
for the first individual.
Figure 10.10. A portion of a NONMEM table. The line numbers on the left are not actually part of the report.
Each row in the table corresponds to a record of
the input file, and the rows appear in the same order as do
the corresponding records of the input data file. Note that
the values of RES and WRES are always shown as zero for
non-observation records†, whereas a (possibly)
nonzero value of PRED is printed for every record.
----------

If there are more than 900 data records, separate
tables are produced for groups of 900 records. The last
table contains the remaining records. If the rows of the
table are sorted, each group of records is sorted
separately. When the input data file is large, the table
will require many pages to print. Therefore, the $TABLE
record should be omitted unless needed for diagnostic
purposes (such as when initially checking a new data set or
model).
7.2. Output from the Scatterplot Step
Many examples of scatterplots are present in
Chapters 2 and 11. They are not reproduced here. Whereas all
the records in the input data file correspond to rows of a
table, this is not true of a scatterplot that includes one
or more of the items RES, WRES, and DV. When one of these
three is being plotted, then only observation records
contribute points to the scatterplot†.
----------
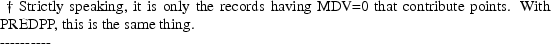
In figure 2.5, there are exactly 10 points
"*", corresponding to the 10 observation records
in figure 2.2; the dose record does not contribute a
point.
NONMEM displays only the first 900 records of the
appropriate type in a scatterplot. This limit applies before
any partitioning. For example, in a plot of DV VS ID, the
first 900 observation records are displayed; in a plot of WT
vs ID, the first 900 records of the data file are displayed.
Additional scatterplots can be requested, showing additional
points, using options "FROM=" and "TO="
of the $SCATTERPLOT record. See NONMEM Users Guide, Part
IV.
TOP
TABLE OF CONTENTS
NEXT
 ; DV is
; DV is
 ; PRED is
; PRED is
 (evaluated for the typical
individual in the population). Line 24 shows the format used
to read each data record. In this example, the format was
generated by the Data Preprocessor and describes the data
file after processing by the Data Preprocessor.†
----------
(evaluated for the typical
individual in the population). Line 24 shows the format used
to read each data record. In this example, the format was
generated by the Data Preprocessor and describes the data
file after processing by the Data Preprocessor.†
----------
 ,
,
 and
and
 are given (lines 29, 31 and
33), then their initial estimates are displayed. In lines
38-41, notice the values 0.1000e+07 and -0.1000e+07. These
are NONMEM’s way of expressing the values
are given (lines 29, 31 and
33), then their initial estimates are displayed. In lines
38-41, notice the values 0.1000e+07 and -0.1000e+07. These
are NONMEM’s way of expressing the values
 and
and
 ; i.e., of describing
; i.e., of describing
 s which are unbounded on
one or both sides. Another FORTRAN system may display these
numbers differently (e.g., 1.0000e+06), but the absolute
value will always be 1,000,000. In lines 43 and 44, notice
that the variances from the $OMEGA record appear along the
diagonal of the
s which are unbounded on
one or both sides. Another FORTRAN system may display these
numbers differently (e.g., 1.0000e+06), but the absolute
value will always be 1,000,000. In lines 43 and 44, notice
that the variances from the $OMEGA record appear along the
diagonal of the  matrix, and
that the off-diagonal element
matrix, and
that the off-diagonal element
 is zero. Line 31 states
that NONMEM understands
is zero. Line 31 states
that NONMEM understands  to
be diagonal; the off-diagonal element(s) are automatically
fixed at zero.
to
be diagonal; the off-diagonal element(s) are automatically
fixed at zero. ,
,
 , and
, and
 . Line 51 displays the
desired number of significant digits in the final parameter
estimate; the value 3 is the default number requested by
NM-TRAN.
. Line 51 displays the
desired number of significant digits in the final parameter
estimate; the value 3 is the default number requested by
NM-TRAN.
 whatsoever (directly or
indirectly). NM-TRAN has instructed PREDPP that the $ERROR
statements need be evaluated only once at the beginning of
the problem. Line 20 indicates that, should the Simulation
Step be implemented, PREDPP will disregard this limitation
and evaluate the $ERROR statements with every event record,
so that randomly-generated values of intra-individual error
can be applied at every observation event. (This example
does not involve simulation, but the PK and ERROR routines
which implement the $PK and $ERROR statements are capable of
supporting all NONMEM tasks, including
simulation.)
whatsoever (directly or
indirectly). NM-TRAN has instructed PREDPP that the $ERROR
statements need be evaluated only once at the beginning of
the problem. Line 20 indicates that, should the Simulation
Step be implemented, PREDPP will disregard this limitation
and evaluate the $ERROR statements with every event record,
so that randomly-generated values of intra-individual error
can be applied at every observation event. (This example
does not involve simulation, but the PK and ERROR routines
which implement the $PK and $ERROR statements are capable of
supporting all NONMEM tasks, including
simulation.) ,
and then divided by
,
and then divided by 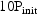 (scaled), where
(scaled), where 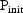 is the
transformed initial estimate of the parameter. The result of
this two-stage conversion is a new parameter called the
scaled transformed parameter (STP). Thus, in line 6,
all parameters are .1 at the 0-th iteration. Parameters are
printed in the following order: elements of
is the
transformed initial estimate of the parameter. The result of
this two-stage conversion is a new parameter called the
scaled transformed parameter (STP). Thus, in line 6,
all parameters are .1 at the 0-th iteration. Parameters are
printed in the following order: elements of
 , elements of
, elements of
 , elements of
, elements of
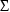 . In this example, reading
from left to right, the parameters are
. In this example, reading
from left to right, the parameters are
 ,
,
 ,
,
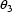 ,
,
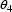 ,
,
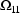 ,
,
 , and
, and
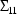 .
. ,
which is effectively fixed to 0, does not appear. Second,
when off-diagonal elements of
,
which is effectively fixed to 0, does not appear. Second,
when off-diagonal elements of
 are being estimated, then
as many additional STP’s appear as there are
off-diagonal elements of
are being estimated, then
as many additional STP’s appear as there are
off-diagonal elements of  being estimated. However, a 1-1 correspondence between each
of the elements of
being estimated. However, a 1-1 correspondence between each
of the elements of  and an
STP does not exist. The same is true for elements of
and an
STP does not exist. The same is true for elements of
 and the STP’s for
and the STP’s for
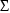 when off-diagonal elements
of
when off-diagonal elements
of 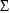 are
estimated.
are
estimated. , is
an exception. It is clearly approaching a very small value
close to its lower bound, 0. In Chapter 12, we shall see
that both
, is
an exception. It is clearly approaching a very small value
close to its lower bound, 0. In Chapter 12, we shall see
that both 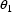 and
and
 are best fixed at
0.)
are best fixed at
0.)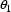 STP estimate
is .949e-10, and so the 949 are not significant digits at
all! Because NONMEM displays only 3 significant digits in
the printed parameter estimates, and for other reasons as
well, by default NM-TRAN requests only 3 significant digits.
However, more significance can be requested, as was
discussed in Chapter 9, Section 4.1.
STP estimate
is .949e-10, and so the 949 are not significant digits at
all! Because NONMEM displays only 3 significant digits in
the printed parameter estimates, and for other reasons as
well, by default NM-TRAN requests only 3 significant digits.
However, more significance can be requested, as was
discussed in Chapter 9, Section 4.1. ’s, or the data may be incorrect; see Chapter
11.
’s, or the data may be incorrect; see Chapter
11.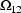 ) that
is 0 by definition, rather than due to a
computation.
) that
is 0 by definition, rather than due to a
computation.