1. What This Chapter is About
2. Model Fitting Criterion
2.1. Least Squares for Individual Data with an Additive Error Model
2.2. Least Squares for Individual Data with Other Types of Error Models
2.3. Least Squares for Population Data
3. Parameter Estimates
4. Precision of Parameter Estimates
4.1. Distribution of Parameters vs Distribution of Parameter Estimates
4.2. Confidence Interval for a Single Parameter
4.2.1. Estimating a Parameter’s Standard Error
4.2.2. Relating the Confidence Interval to the 
4.2.3. A Confidence Interval for a Function of a Single Parameter
4.3. Multiple Parameters
4.3.1. Correlation of Parameter Estimates
4.3.2. Confidence Intervals for a Function of Several Parameters
5. Hypothesis Testing
5.1. Hypothesis Testing Using the 
5.2. Hypothesis Testing Using the Likelihood Ratio
5.2.1. Definition — Full/Reduced Models
5.2.2. Reduced/Full Models Express the Null/Alternative Hypotheses
5.2.3. The Likelihood Ratio Test
6. Choosing Among Models
NONMEM Users Guide Part V - Introductory Guide
- Chapter 5
Chapter 5 - Estimates, Confidence
Intervals, and Hypothesis Tests
1. What This Chapter is About
In this chapter, we discuss the fitting criterion
that NONMEM uses, parameter estimates, and standard error
estimates. We then discuss how to form confidence intervals
for parameters and do hypothesis tests with
NONMEM.
2. Model Fitting Criterion
In principle, all fitting procedures attempt to
adjust the values of the parameters of the model to give a
"best fit" of the predictions to the actual
observations. The set of parameters that accomplish this are
called the parameter estimates, and are denoted here as
 ,
,
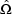 , and
, and
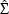 . Methods differ in how they
define "best". The criterion that NONMEM uses is a
Least Squares (LS) type criterion. The form of this
criterion varies as the error model varies, and as
population models with multiple random effects must be
considered. We briefly discuss these various criteria next,
to give the reader a feel for what NONMEM is doing. A
detailed knowledge of the statistical basis for the choice
of fitting criterion is not necessary either to use or
interpret NONMEM fits. In this chapter, a fixed effects
parameter will be denoted by a
. Methods differ in how they
define "best". The criterion that NONMEM uses is a
Least Squares (LS) type criterion. The form of this
criterion varies as the error model varies, and as
population models with multiple random effects must be
considered. We briefly discuss these various criteria next,
to give the reader a feel for what NONMEM is doing. A
detailed knowledge of the statistical basis for the choice
of fitting criterion is not necessary either to use or
interpret NONMEM fits. In this chapter, a fixed effects
parameter will be denoted by a
 ; the distinction between
individual fixed effects parameters (
; the distinction between
individual fixed effects parameters (
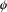 ) and population fixed
effects parameters will not be important here.
) and population fixed
effects parameters will not be important here.
2.1. Least Squares for Individual Data with an Additive Error Model
For the Additive error model (3.4), the Ordinary
Least Squares criterion (OLS) chooses the estimate
 so as to make the sum of
squared (estimated) errors as small as possible. These
estimates cause the prediction, here denoted
so as to make the sum of
squared (estimated) errors as small as possible. These
estimates cause the prediction, here denoted
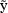 , to be an estimate of the
mean value of
, to be an estimate of the
mean value of 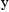 , which is
intuitively appealing. The prediction is obtained by
computing the value for y under the model with parameters
set to their estimated values and
, which is
intuitively appealing. The prediction is obtained by
computing the value for y under the model with parameters
set to their estimated values and
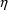 set to zero†.
set to zero†.
----------

2.2. Least Squares for Individual Data with Other Types of Error Models
The simple OLS criterion just defined becomes
inefficient and is no longer the "best" one to use
when the error model is other than the Additive error model.
It treats all estimated errors as equally important (i.e. a
reduction in the magnitude of either of two estimated errors
that are of the same magnitude is equally valuable in that
either reduction decreases the sum of squared errors by the
same amount), and this results in parameter estimates that
cause all errors to have about the same typical magnitude,
as assumed under the Additive model. The CCV error model,
though, says that the typical magnitude of an error varies
monotonically with the magnitude of the (true) prediction of
y. In principle, Weighted Least Squares (WLS) gives a fit
more commensurate with the CCV or other non-Additive error
model. WLS chooses  as that
value of
as that
value of  minimizing
minimizing
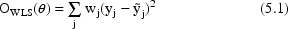
Each 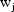 is a weight
which, ideally, is set proportional to the inverse of the
variance of
is a weight
which, ideally, is set proportional to the inverse of the
variance of  . In the CCV
model this variance is proportional to
. In the CCV
model this variance is proportional to
 (evaluated at the true
value of
(evaluated at the true
value of  ). Use of such
weights will down-weight the importance of estimated squared
errors associated with large values of
). Use of such
weights will down-weight the importance of estimated squared
errors associated with large values of
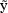 and promote the relative
contribution of those associated with small values of
and promote the relative
contribution of those associated with small values of
 .
.
In many cases, users can supply approximate
weights, and the WLS objective function can be used as
stated in (5.1). When, as with the CCV model for example,
the ideal weights depend on the true values of parameters,
these true values can be replaced by initial estimates, and
then the WLS objective function as given in (5.1) can be
minimized. Alternatively, instead of viewing
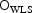 as a function of
as a function of
 only through the estimated
error’s dependence on
only through the estimated
error’s dependence on  , it can be viewed as a function of
, it can be viewed as a function of
 through both that
dependence and also through the ideal weights’
dependence on
through both that
dependence and also through the ideal weights’
dependence on  . The entire
function can then be minimized with respect to
. The entire
function can then be minimized with respect to
 . That this creates a
problem is most easily seen when the error model contains a
parameter which is not itself a parameter of the structural
model, but which, nonetheless, must be regarded as an
element of
. That this creates a
problem is most easily seen when the error model contains a
parameter which is not itself a parameter of the structural
model, but which, nonetheless, must be regarded as an
element of  . Such an error
model is the Power Function model of (3.7), and the
"extra" parameter is
. Such an error
model is the Power Function model of (3.7), and the
"extra" parameter is
 . The WLS objective
function with the reciprocal variance of
. The WLS objective
function with the reciprocal variance of
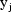 substituted for
substituted for
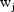 is†
is†
----------
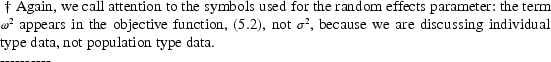

In this case if 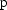 were set to a very large number, while the other parameters
in
were set to a very large number, while the other parameters
in  were only such as to
make all
were only such as to
make all 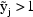 , then all
, then all
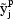 would be very large, and
the summation would attain a very small value. (The value of
would be very large, and
the summation would attain a very small value. (The value of
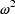 is irrelevant to the
minimization with respect to
is irrelevant to the
minimization with respect to
 .) Thus, all elements in
.) Thus, all elements in
 other than
other than
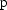 would be indeterminate (as
long as they were such that all
would be indeterminate (as
long as they were such that all
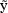 were greater than 1); a
most unsatisfactory state of affairs.
were greater than 1); a
most unsatisfactory state of affairs.
There is a way to deal with this problem that
preserves the spirit of least-squares fitting, and NONMEM
uses it. In essence, it adds to the WLS objective function a
term proportional to the sum of the logarithms of the error
variances. Thus a penalty is paid for increasing the error
variances without a concomitant decrease in the estimated
errors themselves. This modified objective function is
called the Extended Least Squares (ELS) objective function.
It is minimized with respect to all parameters of the
structural and error models simultaneously (in the current
example,  and
and
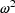 , as
, as
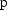 can be considered an
element of
can be considered an
element of  ).
).
2.3. Least Squares for Population Data
The complications arising from a population model
are due entirely to the random interindividual effects
occurring in the parameter model. To deal with this, NONMEM
uses an approximation to the true model. The approximate
model is linear in all the random effects. For this
linearized model, the vector of mean values for the
observations from the 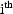 individual is the vector of true predictions for these
observations. These predictions are obtained from the model
by setting the parameters to their true values and by
setting all the elements of both
individual is the vector of true predictions for these
observations. These predictions are obtained from the model
by setting the parameters to their true values and by
setting all the elements of both
 and
and
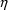 to zero. In other words,
these are the true predictions for the mean individual with
fixed effects equal to those of the
to zero. In other words,
these are the true predictions for the mean individual with
fixed effects equal to those of the
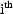 individual. For this
linearized model it is also possible to write a formula for
the variance-covariance matrix of the observations from the
individual. For this
linearized model it is also possible to write a formula for
the variance-covariance matrix of the observations from the
 individual. This matrix is
a function of the individual’s fixed effects and the
population parameters
individual. This matrix is
a function of the individual’s fixed effects and the
population parameters  ,
,
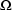 , and
, and
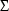 . Finally, the ELS
objective function discussed above is generalized to be a
sum over individuals, rather than observations, and where
the
. Finally, the ELS
objective function discussed above is generalized to be a
sum over individuals, rather than observations, and where
the 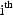 term of the sum
involves a squared error between a vector of observations
and an associated vector of predictions, weighted by the
reciprocal of the associated variance-covariance matrix for
the
term of the sum
involves a squared error between a vector of observations
and an associated vector of predictions, weighted by the
reciprocal of the associated variance-covariance matrix for
the 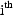 individual.
individual.
3. Parameter Estimates
It is useful to consider how to estimate
parameters that do not appear in the model we use to fit the
data, but are, instead, functions of them (e.g. the
half-life parameter 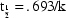 , when
the rate constant of elimination
, when
the rate constant of elimination
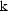 is the model
parameter).
is the model
parameter).
It is always possible, of course, to parameterize
the model in the function of interest. For example, we have
already seen (Chapters 2 & 3) that we may use the
function (parameter) 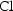 in the
one-compartment model instead of
in the
one-compartment model instead of
 . However, we may be
interested in the values of several alternative
parameterizations (e.g., we may want to know k, clearance,
and half-life). Rather than rerun the same problem with
several alternative parameterizations, we can use the fact
that the LS estimate of a function of the parameters is
given by the same function of the LS parameter estimates.
Formally, if
. However, we may be
interested in the values of several alternative
parameterizations (e.g., we may want to know k, clearance,
and half-life). Rather than rerun the same problem with
several alternative parameterizations, we can use the fact
that the LS estimate of a function of the parameters is
given by the same function of the LS parameter estimates.
Formally, if 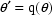 is the
function of interest, then
is the
function of interest, then  . E.g. Letting
. E.g. Letting 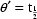 ,
,
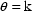 , and
, and
 , then
, then
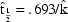 .
.
4. Precision of Parameter Estimates
Clearly, it is almost impossible for the
estimates to actually be the true values. The question is:
how far are the true values from the estimates? To discuss
this question, imagine replicating the entire experiment
(gathering new data, but keeping
 fixed) multiple times.
Also, for simplicity, imagine that the model has only one
scalar parameter,
fixed) multiple times.
Also, for simplicity, imagine that the model has only one
scalar parameter,  , and
that its true value,
, and
that its true value, 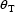 is
known. If, after each replication, the estimate of
is
known. If, after each replication, the estimate of
 is recorded, and a
histogram of these values is plotted, one might see
something like figure 5.1A or 5.1B.
is recorded, and a
histogram of these values is plotted, one might see
something like figure 5.1A or 5.1B.
Figure 5.1. Two hypothetical histograms of estimates of a single parameter upon replication of a given experiment. Left panel (A): The estimates have small variance (spread) but are biased (the mean of the estimates differs from the true value, θ); Right panel: The estimates have large variance but are relatively unbiased.
The difference between the estimate and the true
value, 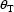 , obviously differs
from replication to replication. Let this difference be
called the estimation error. We cannot know the
estimation error of any particular estimate (if we could, we
could know the true value itself, by subtraction), but we
can hope to estimate the mean error magnitude. Since errors
can be positive or negative, a measure of magnitude that is
unaffected by sign is desirable. This is traditionally the
Mean Squared Error (
, obviously differs
from replication to replication. Let this difference be
called the estimation error. We cannot know the
estimation error of any particular estimate (if we could, we
could know the true value itself, by subtraction), but we
can hope to estimate the mean error magnitude. Since errors
can be positive or negative, a measure of magnitude that is
unaffected by sign is desirable. This is traditionally the
Mean Squared Error ( 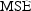 ). The
MSE can be factored into two parts:
). The
MSE can be factored into two parts:

where 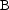 is the
bias of the estimates (mean (signed) difference between the
estimates and the true value) and
is the
bias of the estimates (mean (signed) difference between the
estimates and the true value) and
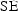 is the standard error of
the estimates (
is the standard error of
the estimates ( 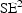 is the
variance of the estimates). As illustrated in figure 5.1,
the
is the
variance of the estimates). As illustrated in figure 5.1,
the 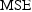 can be about the same
for two types of estimates while both their bias and
can be about the same
for two types of estimates while both their bias and
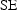 differ. It is very hard to
estimate the bias of an estimator unless the true parameter
value is, in fact, known. This is not true of the
differ. It is very hard to
estimate the bias of an estimator unless the true parameter
value is, in fact, known. This is not true of the
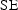 : the standard deviation of
the distribution of estimates of a parameter on replication
is the
: the standard deviation of
the distribution of estimates of a parameter on replication
is the  ; no knowledge of
the true value of the parameter is required. In many
situations, LS estimators of fixed effects parameters are
unbiased, although in nonlinear problems, such as most
pharmacokinetic ones, this cannot be assured.
; no knowledge of
the true value of the parameter is required. In many
situations, LS estimators of fixed effects parameters are
unbiased, although in nonlinear problems, such as most
pharmacokinetic ones, this cannot be assured.
4.1. Distribution of Parameters vs Distribution of Parameter Estimates
Figure 5.1 illustrates the distribution of
parameter estimates that might result if an experiment were
replicated. The bias and spread depend on the estimation
method, the design of the experiment (
 , which implicitly includes
, which implicitly includes
 ) and on the true parameter
values, including the variances (and covariances) of the
random effects influencing
) and on the true parameter
values, including the variances (and covariances) of the
random effects influencing 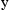 . If, for example, more observations were obtained in each
experiment (more individuals in a population study), the
spread of the estimates (one from each experiment) would
decrease until, in the limit, if an infinite number of
observations were obtained in each experiment, every
estimate would be the same (equal to the true value plus the
bias of the estimator). Thus, the distribution of the
estimate tells us nothing about biology or measurement
error, but only about the
. If, for example, more observations were obtained in each
experiment (more individuals in a population study), the
spread of the estimates (one from each experiment) would
decrease until, in the limit, if an infinite number of
observations were obtained in each experiment, every
estimate would be the same (equal to the true value plus the
bias of the estimator). Thus, the distribution of the
estimate tells us nothing about biology or measurement
error, but only about the  of the estimate itself.
of the estimate itself.
In contrast,  and
and
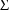 tell us about unexplained
(or random) interindividual variability (biology) or error
magnitude (biology plus measurement error), not about how
precisely we know these things. No matter how many
observations we make, interindividual variability will
remain the same size (but the variability of our estimate of
its size will decrease), as will the measurement error
variability of a particular instrument.
tell us about unexplained
(or random) interindividual variability (biology) or error
magnitude (biology plus measurement error), not about how
precisely we know these things. No matter how many
observations we make, interindividual variability will
remain the same size (but the variability of our estimate of
its size will decrease), as will the measurement error
variability of a particular instrument.
It is very important not to confuse variability
(e.g., between individuals) in a model parameter with
variability in the estimate of that parameter, despite the
fact that the terms we use to describe both variabilities
are similar. Thus an element of
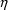 , say
, say
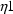 has a
has a
 ,
,
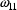 , while the estimate of
, while the estimate of
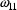 ,
,
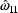 , also has a
, also has a
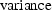 given by the square of the
standard error for
given by the square of the
standard error for 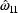 .
Indeed, the use of the term "standard error"
rather than "standard deviation" to name a measure
of the spread in the distribution of the parameter
.
Indeed, the use of the term "standard error"
rather than "standard deviation" to name a measure
of the spread in the distribution of the parameter
 rather than in the
parameter helps call attention to the distinction between
these two types of things.
rather than in the
parameter helps call attention to the distinction between
these two types of things.
4.2. Confidence Interval for a Single Parameter
Acknowledging that any particular estimate from
any particular experiment is unlikely to equal the true
parameter value implies that we should be interested in
"interval" estimates of parameters as well as
(instead of?) point estimates. An interval estimate of a
parameter is usually a range of values for the parameter,
often centered at the point estimate, such that the range
contains the true parameter value with a specified
probability. The probability chosen is often 95%, in which
case the interval estimate is called the 95% Confidence
Interval (CI).
A CI is often based only on the parameter
estimate and its 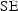 . In the
next sections we discuss three questions about such CIs a
little further. (i) How to estimate the
. In the
next sections we discuss three questions about such CIs a
little further. (i) How to estimate the
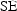 from a single set of data
(we cannot replicate our experiment many times and construct
a histogram as in figure 5.1). (ii) Given an estimate of
from a single set of data
(we cannot replicate our experiment many times and construct
a histogram as in figure 5.1). (ii) Given an estimate of
 , how to use that number
to compute a (95% confidence) interval with 95% chance of
containing the true parameter value. (iii) Given an estimate
of
, how to use that number
to compute a (95% confidence) interval with 95% chance of
containing the true parameter value. (iii) Given an estimate
of 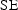 , how to compute a
confidence interval for a function of the
parameter.
, how to compute a
confidence interval for a function of the
parameter.
4.2.1. Estimating a Parameter’s Standard Error
Remarkably, the 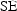 of a parameter estimate can be estimated using only the data
from a single experiment. The idea is that the data give us
estimates of the variances of all random effects in our
model, from which we can estimate the variability in future
data (if we were to replicate the experiment). That is, the
SE of the estimates on replication depends only on
quantities we either know or have estimates of: the
of a parameter estimate can be estimated using only the data
from a single experiment. The idea is that the data give us
estimates of the variances of all random effects in our
model, from which we can estimate the variability in future
data (if we were to replicate the experiment). That is, the
SE of the estimates on replication depends only on
quantities we either know or have estimates of: the
 , the number of
, the number of
 observed (
observed (
 ), and the variances of
all random effects.
), and the variances of
all random effects.
It is a little beyond the scope of this
discussion to give the method by which NONMEM actually
estimates the 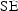 of a
parameter estimate; however, examples of how this can be
done are found in any statistical textbook on regression.
NONMEM presents the estimated standard error for each
parameter of the model (including the random effects
parameters,
of a
parameter estimate; however, examples of how this can be
done are found in any statistical textbook on regression.
NONMEM presents the estimated standard error for each
parameter of the model (including the random effects
parameters,  and
and
 ) as part of its
output.
) as part of its
output.
4.2.2. Relating the Confidence Interval to the 
Statistical theory tells us not only how to
compute the 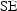 of a parameter
estimate, but also that for a LS estimate (and many other
kinds of estimates), the shape of the distribution of the
estimates is approximately Normal if the data set is large
enough. This means that we may use percentiles of the Normal
distribution, to compute confidence interval bounds (when
of a parameter
estimate, but also that for a LS estimate (and many other
kinds of estimates), the shape of the distribution of the
estimates is approximately Normal if the data set is large
enough. This means that we may use percentiles of the Normal
distribution, to compute confidence interval bounds (when
 is small, the
is small, the
 distribution is often used
instead; this is discussed in statistics texts). In general,
a 100(1-
distribution is often used
instead; this is discussed in statistics texts). In general,
a 100(1-  )% confidence
interval for a single parameter,
)% confidence
interval for a single parameter,
 say, is computed as
say, is computed as
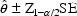 . Here
. Here
 denotes the
denotes the
 percentile of the Normal
distribution. As previously noted,
percentile of the Normal
distribution. As previously noted,
 is often chosen to be .05,
in which case
is often chosen to be .05,
in which case 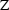 is
approximately 2.
is
approximately 2.
4.2.3. A Confidence Interval for a Function of a Single Parameter
As discussed above, one can reparameterize the
model in terms of the new parameter, and NONMEM will then
estimate its standard error. If re-running the fit presents
a problem, there is a simple way to compute a confidence
interval for a function  of
a single parameter. If the lower and upper bounds of a
100(1-
of
a single parameter. If the lower and upper bounds of a
100(1-  )% confidence
interval for
)% confidence
interval for 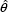 are denoted
are denoted
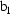 and
and
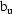 , respectively, then a
100(1-
, respectively, then a
100(1-  )% confidence
interval for
)% confidence
interval for 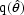 has lower and
upper bounds
has lower and
upper bounds 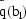 and
and
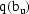 , respectively. This
confidence interval, however, is not necessarily centered at
, respectively. This
confidence interval, however, is not necessarily centered at
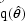 .
.
4.3. Multiple Parameters
4.3.1. Correlation of Parameter Estimates
A truly new feature introduced by multiple
parameters is the phenomenon of correlation among parameter
estimates. NONMEM outputs a correlation matrix for the
parameter estimates. The 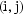 element of the matrix is the correlation between the ith and
jth parameter estimates. A large correlation (e.g.
element of the matrix is the correlation between the ith and
jth parameter estimates. A large correlation (e.g.
 ) means that the
conditional distribution of the ith estimate, given a fixed
value of the jth estimate, depends considerably on this
fixed value. Sometimes each parameter estimate of a pair
that is highly correlated has a large standard error,
meaning that neither parameter can be well-estimated. This
problem may be caused by data that do not distinguish among
the parameters very well, while a simpler model, or a
different design, or more data might permit more precise
estimates of each.
) means that the
conditional distribution of the ith estimate, given a fixed
value of the jth estimate, depends considerably on this
fixed value. Sometimes each parameter estimate of a pair
that is highly correlated has a large standard error,
meaning that neither parameter can be well-estimated. This
problem may be caused by data that do not distinguish among
the parameters very well, while a simpler model, or a
different design, or more data might permit more precise
estimates of each.
As a simple example, imagine a straight line fit
to just two points, both at the same value of
 : neither slope nor
intercept can be estimated at all as long as the other is
unknown, but fixing either one (simplifying the model)
determines the other. Both parameters could be estimated by
observing another point at some other value of
: neither slope nor
intercept can be estimated at all as long as the other is
unknown, but fixing either one (simplifying the model)
determines the other. Both parameters could be estimated by
observing another point at some other value of
 (more data), or, still
using just 2 points, by placing these points at two
different values of
(more data), or, still
using just 2 points, by placing these points at two
different values of  (modifying the design). Thus, when standard errors are
large, it is useful to examine the correlation matrix of
parameter estimates to see, in particular, if some
simplification of the model may help.
(modifying the design). Thus, when standard errors are
large, it is useful to examine the correlation matrix of
parameter estimates to see, in particular, if some
simplification of the model may help.
4.3.2. Confidence Intervals for a Function of Several Parameters
There is an approximate formula for computing a
standard error, and hence a confidence interval for a
function of several parameters (e.g., a confidence interval
for half-life when the estimated parameters are
 and
and
 ). It uses the standard
errors of the parameter estimates and the correlations
between the parameter estimates. However, discussion of this
formula is beyond the scope of this introduction. If a
confidence interval for a function of several parameters is
desired, it is often more convenient to re-fit the data with
the model reparameterized to include the function as an
explicit parameter.
). It uses the standard
errors of the parameter estimates and the correlations
between the parameter estimates. However, discussion of this
formula is beyond the scope of this introduction. If a
confidence interval for a function of several parameters is
desired, it is often more convenient to re-fit the data with
the model reparameterized to include the function as an
explicit parameter.
5. Hypothesis Testing
Before going into details, a note of caution is
in order about hypothesis testing in general. The logic of
hypothesis testing is that one sets up a hypothesis about a
parameter’s value, called the null hypothesis,
and asks if the data are sufficiently in conflict with it to
call it into question. If they are, one rejects the null
hypothesis. However, logically, if they are not, one has
simply failed to reject the null hypothesis; one does not
necessarily have sufficient data to accept it. An extreme
example will make this clear. Let the null hypothesis be any
assertion at all about the state of nature. Gather no
evidence bearing on the question. Clearly, the evidence
(which is void) is insufficient to reject the null
hypothesis, but just as clearly, in this case the evidence
provides no support for it either.
In less extreme cases there is a way to view
failure to reject as lending some support to the null
hypothesis, but the matter is problematic. It is somewhat
less problematic to use a confidence interval to quantify
support for a null hypothesis. A null hypothesis is an
assertion that a parameter’s true value is found among
a set of null values. A confidence interval puts
reasonable bounds on the possible values of a parameter. One
can then say that the evidence (the data from which the
parameter estimate is derived) does support a null
hypothesis (about the value of the parameter) if the null
values are included in the interval and that the evidence
fully support the null hypothesis if all nonnull values lie
outside. An example will help make this clear.
Consider that mean drug clearance in adults
varies linearly with the weight of the individual to a
clinically significant degree. Formally, this can be
put as a statement about a regression coefficient in a model
such as
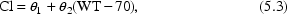
The null hypothesis might be that
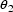 is close to zero, i.e.
that it is not so different from zero as to be clinically
significant. To make this precise, suppose that we know that
mean clearance for a 70 kg person (i.e.,
is close to zero, i.e.
that it is not so different from zero as to be clinically
significant. To make this precise, suppose that we know that
mean clearance for a 70 kg person (i.e.,
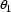 ) is about 100 ml/min. If
) is about 100 ml/min. If
 were .20 ml/min/kg or
less, a 50 kg increment (decrement) in weight from 70 kg
would be associated with less than a 10% change in total
clearance. This is clinically insignificant, so the
appropriate null values for
were .20 ml/min/kg or
less, a 50 kg increment (decrement) in weight from 70 kg
would be associated with less than a 10% change in total
clearance. This is clinically insignificant, so the
appropriate null values for
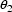 might be 0.0 to .20,
assuming, of course, that a physical lower bound for the
parameter is zero. (More usually in statistical discussions
a set of null values consists of a single number, e.g. 0.)
If the confidence interval for
might be 0.0 to .20,
assuming, of course, that a physical lower bound for the
parameter is zero. (More usually in statistical discussions
a set of null values consists of a single number, e.g. 0.)
If the confidence interval for
 only includes null values
(e.g., it is .10 to .15), one might then safely conclude
that weight, if it has any effect at all, has no
only includes null values
(e.g., it is .10 to .15), one might then safely conclude
that weight, if it has any effect at all, has no
 significant effect, and
that the data fully support the null hypothesis. If the
confidence interval includes null values and others (e.g.,
it is 0.0 to .60), one would conclude that there is some
support for the null hypothesis, but that there is also some
support for rejecting it. In this case the data are
insufficient to allow outright acceptance or rejection. If
the confidence interval includes no null values (e.g., it is
.80 to 1.3), one would reject the null hypothesis and
conclude that weight has a clinically significant (linear)
effect on clearance.
significant effect, and
that the data fully support the null hypothesis. If the
confidence interval includes null values and others (e.g.,
it is 0.0 to .60), one would conclude that there is some
support for the null hypothesis, but that there is also some
support for rejecting it. In this case the data are
insufficient to allow outright acceptance or rejection. If
the confidence interval includes no null values (e.g., it is
.80 to 1.3), one would reject the null hypothesis and
conclude that weight has a clinically significant (linear)
effect on clearance.
For these reasons, we urge caution when
performing hypothesis tests and suggest that confidence
intervals are often more useful. None the less, the
popularity of hypothesis tests requires that they be done,
and we now describe two methods for so doing, the first
somewhat more approximate and less general than the second,
but easier to do.
5.1. Hypothesis Testing Using the 
A straight-forward way to test a null hypothesis
about the value of a parameter is to use a confidence
interval for this purpose. In other words, if the confidence
interval excludes the null values, then the null hypothesis
is rejected. As described in Section 4.2.2, such a
confidence interval is based on the estimated standard
error. This method generalizes to a hypothesis about the
values of several parameters simultaneously, but this is
beyond the scope of this introduction.
5.2. Hypothesis Testing Using the Likelihood Ratio
An approach that involves the extra effort of
re-fitting the data has the advantage of being less
approximate than the one that uses a confidence interval
based on the SE. This method is the so-called Likelihood
Ratio Test.
The basic idea is to compare directly the
goodness of fit (as indicated by the minimum value of the
extended least squares objective function) obtained between
using a model in which the parameter is fixed to the
hypothesized value (the reduced model) and a model in
which the parameter must be estimated (the full
model).
5.2.1. Definition — Full/Reduced Models
A model is a reduced model of a full model if it
is identical to the full model except that one or more
parameters of the latter have been fixed to hypothesized
values (usually 0). Consider the examples:
|
E.g. #1. Valid Full/Reduced Pair:
|
|
Full model:
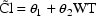
Reduced model:

|
|
E.g. #2. Invalid Full/Reduced Pair:
|
|
Full model:
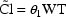
Reduced model:
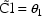
|
In example #1, fixing
 to 0 produces the reduced
model, while in example #2, no parameter of the full model
can be fixed to a particular value to yield the
"reduced" model. It will always be true that if
the models are set up correctly, the number of parameters
that must be estimated will be greater in the full model
than in the reduced model. Note that this is not so for
example #2.
to 0 produces the reduced
model, while in example #2, no parameter of the full model
can be fixed to a particular value to yield the
"reduced" model. It will always be true that if
the models are set up correctly, the number of parameters
that must be estimated will be greater in the full model
than in the reduced model. Note that this is not so for
example #2.
5.2.2. Reduced/Full Models Express the Null/Alternative Hypotheses
The reduced model expresses the null
hypothesis; the full model expresses an alternative
hypothesis. In example #1 above, the null hypothesis is
"typical value of clearance is independent of
weight", and the alternative is "typical value of
clearance depends linearly on weight."
Note an important point here: the alternative
hypothesis represents a particular alternative, and
the likelihood ratio test using it will most sensitively
reject the null hypothesis only when this particular
alternative holds. If the full model were that "the
typical value of clearance is inversely proportional to
weight" (so that as weight increases, the typical value
of clearance decreases, a situation which rarely holds), the
likelihood ratio test using the alternative we have stated
would not be particularly sensitive to rejecting the null
hypothesis, and we might fail to do so. In contrast, we
might succeed in rejecting the null hypothesis if we used
some other alternative model closer to the
truth.
5.2.3. The Likelihood Ratio Test
Part of the NONMEM output is the "Minimum
Value of the Objective Function" (see Chapter 2).
Denote this by 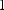 . If
NONMEM’s approximate model were the true model, then
. If
NONMEM’s approximate model were the true model, then
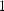 would be minus twice the
maximum logarithm of the likelihood of the data (for those
readers unfamiliar with likelihoods, and curious as to what
they are, we suggest consulting a statistics textbook).
Statistical theory tells us that the difference in minus
twice the maximum log likelihoods between a full and reduced
model can be referenced to a known distribution. Thus, to
perform the Likelihood Ratio Test, one proceeds as
follows.
would be minus twice the
maximum logarithm of the likelihood of the data (for those
readers unfamiliar with likelihoods, and curious as to what
they are, we suggest consulting a statistics textbook).
Statistical theory tells us that the difference in minus
twice the maximum log likelihoods between a full and reduced
model can be referenced to a known distribution. Thus, to
perform the Likelihood Ratio Test, one proceeds as
follows.
Let  be the
minimum value of the objective function from the fit to the
full model, and let
be the
minimum value of the objective function from the fit to the
full model, and let 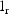 be the
corresponding quantity from the fit to the reduced model.
Fit both models separately yielding
be the
corresponding quantity from the fit to the reduced model.
Fit both models separately yielding
 and
and
 , and form the
statistic,
, and form the
statistic,
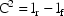
This statistic is approximately distributed
chi-square ( 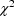 ) with
) with
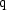 degree of freedom, where
degree of freedom, where
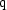 is the number of
parameters whose values are fixed in the reduced model. For
an
is the number of
parameters whose values are fixed in the reduced model. For
an  -level test, compare
-level test, compare
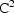 to
to
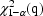 , the 100(1-
, the 100(1-
 ) percentile of the
) percentile of the
 distribution.
distribution.
In particular, when exactly one parameter of the
full model is fixed in the reduced model, a decrease of 3.84
in the minimum value of the objective function is
significant at  .
.
If NONMEM’s approximate model (linear in
the random effects) were the true model, and in addition,
 were linear in the fixed
effects, then
were linear in the fixed
effects, then  would be
(approximately) distributed according to the
would be
(approximately) distributed according to the
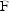 distribution with
distribution with
 , and
, and
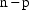 degrees of freedom (
degrees of freedom (
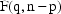 ). Since
). Since
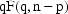 is equal to
is equal to
 only when
only when
 is "large", and
is greater otherwise, it is more conservative to reference
is "large", and
is greater otherwise, it is more conservative to reference
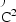 to
to
 in all instances, even
when
in all instances, even
when 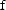 is
nonlinear.
is
nonlinear.
6. Choosing Among Models
An idea related to hypothesis testing is this:
when faced with alternative explanations (models) for some
data, how does one use the data to determine which model(s)
is (are) most plausible? When one of the models is a reduced
sub-model of the other, and there is some
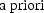 reason to prefer the
reduced model to the alternative, then the Likelihood Ratio
test can be used to test whether this a priori preference
must be rejected (at the
reason to prefer the
reduced model to the alternative, then the Likelihood Ratio
test can be used to test whether this a priori preference
must be rejected (at the  level). However, when one gives the matter some thought,
there is usually little objective reason to prefer
one model over another on a priori grounds. For example,
although possibly more convenient, a monoexponential model
is, if anything, less likely on biological grounds than a
biexponential.
level). However, when one gives the matter some thought,
there is usually little objective reason to prefer
one model over another on a priori grounds. For example,
although possibly more convenient, a monoexponential model
is, if anything, less likely on biological grounds than a
biexponential.
Not only may there not be a clear
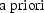 probability favoring one
contending model over another, but the two models may not
form a full and reduced model pair. In such circumstances,
one must rely on some goodness-of-fit criterion to
distinguish between the models. Consider choosing between
just two models (the ideas to be discussed readily
generalize to more than two), denoted model
probability favoring one
contending model over another, but the two models may not
form a full and reduced model pair. In such circumstances,
one must rely on some goodness-of-fit criterion to
distinguish between the models. Consider choosing between
just two models (the ideas to be discussed readily
generalize to more than two), denoted model
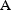 and model
and model
 . If the number of free
parameters in model
. If the number of free
parameters in model 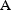 (
(
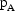 ) is the same as that of
) is the same as that of
 (
(
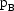 ), then here is a
reasonable criterion: favor the model with the better fit.
Note that there is no
), then here is a
reasonable criterion: favor the model with the better fit.
Note that there is no  value associated with this statement; no hypothesis is being
tested.
value associated with this statement; no hypothesis is being
tested.
Unfortunately, if
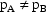 one cannot simply compare
one cannot simply compare
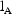 and
and
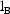 and choose the one with
the smaller value. The reason is best understood when
and choose the one with
the smaller value. The reason is best understood when
 and
and
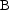 are a full and reduced
model pair. The full model will always fit the data
better (i.e., have a smaller
are a full and reduced
model pair. The full model will always fit the data
better (i.e., have a smaller
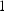 ) as it has more free
parameters to adjust its shape to the data. While the same
is not always true for any pair of non-linear models with
different numbers of parameters, it is often true: the model
with the greater number of parameters will fit a given data
set better than the model with fewer parameters. Yet the
larger (more parameters) model may not really be better; it
may, in fact, fit an entirely new data set worse than the
simpler model if its better fit to the original data was
simply because it exploited the flexibility of its extra
parameter(s) to better fit some random aspect of that
data.
) as it has more free
parameters to adjust its shape to the data. While the same
is not always true for any pair of non-linear models with
different numbers of parameters, it is often true: the model
with the greater number of parameters will fit a given data
set better than the model with fewer parameters. Yet the
larger (more parameters) model may not really be better; it
may, in fact, fit an entirely new data set worse than the
simpler model if its better fit to the original data was
simply because it exploited the flexibility of its extra
parameter(s) to better fit some random aspect of that
data.
Based on the above intuitive argument, it seems
that one should penalize the larger model in some way before
comparing the likelihoods. This intuition is formally
realized in the Akaike Information Criterion (AIC) which
says that one should compute
 +
+
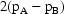 , and choose model
, and choose model
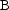 if
if
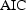 is >0, and model
is >0, and model
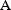 if
if
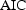 is <0. The second term
penalizes model
is <0. The second term
penalizes model 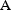 if
if
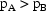 , and vice versa. When
, and vice versa. When
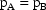 , the
, the
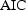 reduces to the comparison
of
reduces to the comparison
of 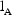 and
and
 described
previously.
described
previously.
TOP
TABLE OF CONTENTS
NEXT
 ,
,
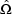 , and
, and
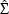 . Methods differ in how they
define "best". The criterion that NONMEM uses is a
Least Squares (LS) type criterion. The form of this
criterion varies as the error model varies, and as
population models with multiple random effects must be
considered. We briefly discuss these various criteria next,
to give the reader a feel for what NONMEM is doing. A
detailed knowledge of the statistical basis for the choice
of fitting criterion is not necessary either to use or
interpret NONMEM fits. In this chapter, a fixed effects
parameter will be denoted by a
. Methods differ in how they
define "best". The criterion that NONMEM uses is a
Least Squares (LS) type criterion. The form of this
criterion varies as the error model varies, and as
population models with multiple random effects must be
considered. We briefly discuss these various criteria next,
to give the reader a feel for what NONMEM is doing. A
detailed knowledge of the statistical basis for the choice
of fitting criterion is not necessary either to use or
interpret NONMEM fits. In this chapter, a fixed effects
parameter will be denoted by a
 ; the distinction between
individual fixed effects parameters (
; the distinction between
individual fixed effects parameters (
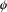 ) and population fixed
effects parameters will not be important here.
) and population fixed
effects parameters will not be important here.

 so as to make the sum of
squared (estimated) errors as small as possible. These
estimates cause the prediction, here denoted
so as to make the sum of
squared (estimated) errors as small as possible. These
estimates cause the prediction, here denoted
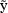 , to be an estimate of the
mean value of
, to be an estimate of the
mean value of 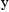 , which is
intuitively appealing. The prediction is obtained by
computing the value for y under the model with parameters
set to their estimated values and
, which is
intuitively appealing. The prediction is obtained by
computing the value for y under the model with parameters
set to their estimated values and
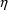 set to zero†.
set to zero†.
 as that
value of
as that
value of  minimizing
minimizing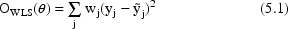
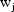 is a weight
which, ideally, is set proportional to the inverse of the
variance of
is a weight
which, ideally, is set proportional to the inverse of the
variance of  . In the CCV
model this variance is proportional to
. In the CCV
model this variance is proportional to
 (evaluated at the true
value of
(evaluated at the true
value of  ). Use of such
weights will down-weight the importance of estimated squared
errors associated with large values of
). Use of such
weights will down-weight the importance of estimated squared
errors associated with large values of
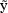 and promote the relative
contribution of those associated with small values of
and promote the relative
contribution of those associated with small values of
 .
. as a function of
as a function of
 only through the estimated
error’s dependence on
only through the estimated
error’s dependence on  , it can be viewed as a function of
, it can be viewed as a function of
 through both that
dependence and also through the ideal weights’
dependence on
through both that
dependence and also through the ideal weights’
dependence on  . The entire
function can then be minimized with respect to
. The entire
function can then be minimized with respect to
 . That this creates a
problem is most easily seen when the error model contains a
parameter which is not itself a parameter of the structural
model, but which, nonetheless, must be regarded as an
element of
. That this creates a
problem is most easily seen when the error model contains a
parameter which is not itself a parameter of the structural
model, but which, nonetheless, must be regarded as an
element of  . Such an error
model is the Power Function model of (3.7), and the
"extra" parameter is
. Such an error
model is the Power Function model of (3.7), and the
"extra" parameter is
 . The WLS objective
function with the reciprocal variance of
. The WLS objective
function with the reciprocal variance of
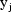 substituted for
substituted for
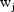 is†
is†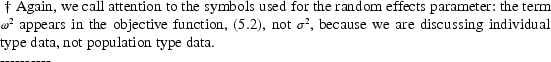

 were set to a very large number, while the other parameters
in
were set to a very large number, while the other parameters
in  were only such as to
make all
were only such as to
make all 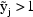 , then all
, then all
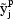 would be very large, and
the summation would attain a very small value. (The value of
would be very large, and
the summation would attain a very small value. (The value of
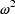 is irrelevant to the
minimization with respect to
is irrelevant to the
minimization with respect to
 .) Thus, all elements in
.) Thus, all elements in
 other than
other than
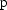 would be indeterminate (as
long as they were such that all
would be indeterminate (as
long as they were such that all
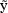 were greater than 1); a
most unsatisfactory state of affairs.
were greater than 1); a
most unsatisfactory state of affairs. and
and
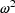 , as
, as
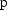 can be considered an
element of
can be considered an
element of  ).
).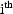 individual is the vector of true predictions for these
observations. These predictions are obtained from the model
by setting the parameters to their true values and by
setting all the elements of both
individual is the vector of true predictions for these
observations. These predictions are obtained from the model
by setting the parameters to their true values and by
setting all the elements of both
 and
and
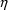 to zero. In other words,
these are the true predictions for the mean individual with
fixed effects equal to those of the
to zero. In other words,
these are the true predictions for the mean individual with
fixed effects equal to those of the
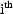 individual. For this
linearized model it is also possible to write a formula for
the variance-covariance matrix of the observations from the
individual. For this
linearized model it is also possible to write a formula for
the variance-covariance matrix of the observations from the
 individual. This matrix is
a function of the individual’s fixed effects and the
population parameters
individual. This matrix is
a function of the individual’s fixed effects and the
population parameters  ,
,
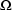 , and
, and
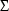 . Finally, the ELS
objective function discussed above is generalized to be a
sum over individuals, rather than observations, and where
the
. Finally, the ELS
objective function discussed above is generalized to be a
sum over individuals, rather than observations, and where
the 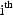 term of the sum
involves a squared error between a vector of observations
and an associated vector of predictions, weighted by the
reciprocal of the associated variance-covariance matrix for
the
term of the sum
involves a squared error between a vector of observations
and an associated vector of predictions, weighted by the
reciprocal of the associated variance-covariance matrix for
the 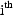 individual.
individual.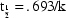 , when
the rate constant of elimination
, when
the rate constant of elimination
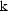 is the model
parameter).
is the model
parameter).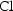 in the
one-compartment model instead of
in the
one-compartment model instead of
 . However, we may be
interested in the values of several alternative
parameterizations (e.g., we may want to know k, clearance,
and half-life). Rather than rerun the same problem with
several alternative parameterizations, we can use the fact
that the LS estimate of a function of the parameters is
given by the same function of the LS parameter estimates.
Formally, if
. However, we may be
interested in the values of several alternative
parameterizations (e.g., we may want to know k, clearance,
and half-life). Rather than rerun the same problem with
several alternative parameterizations, we can use the fact
that the LS estimate of a function of the parameters is
given by the same function of the LS parameter estimates.
Formally, if 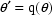 is the
function of interest, then
is the
function of interest, then  . E.g. Letting
. E.g. Letting 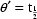 ,
,
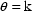 , and
, and
 , then
, then
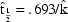 .
. fixed) multiple times.
Also, for simplicity, imagine that the model has only one
scalar parameter,
fixed) multiple times.
Also, for simplicity, imagine that the model has only one
scalar parameter,  , and
that its true value,
, and
that its true value, 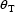 is
known. If, after each replication, the estimate of
is
known. If, after each replication, the estimate of
 is recorded, and a
histogram of these values is plotted, one might see
something like figure 5.1A or 5.1B.
is recorded, and a
histogram of these values is plotted, one might see
something like figure 5.1A or 5.1B.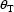 , obviously differs
from replication to replication. Let this difference be
called the estimation error. We cannot know the
estimation error of any particular estimate (if we could, we
could know the true value itself, by subtraction), but we
can hope to estimate the mean error magnitude. Since errors
can be positive or negative, a measure of magnitude that is
unaffected by sign is desirable. This is traditionally the
Mean Squared Error (
, obviously differs
from replication to replication. Let this difference be
called the estimation error. We cannot know the
estimation error of any particular estimate (if we could, we
could know the true value itself, by subtraction), but we
can hope to estimate the mean error magnitude. Since errors
can be positive or negative, a measure of magnitude that is
unaffected by sign is desirable. This is traditionally the
Mean Squared Error ( 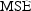 ). The
MSE can be factored into two parts:
). The
MSE can be factored into two parts:
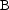 is the
bias of the estimates (mean (signed) difference between the
estimates and the true value) and
is the
bias of the estimates (mean (signed) difference between the
estimates and the true value) and
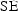 is the standard error of
the estimates (
is the standard error of
the estimates ( 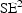 is the
variance of the estimates). As illustrated in figure 5.1,
the
is the
variance of the estimates). As illustrated in figure 5.1,
the 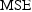 can be about the same
for two types of estimates while both their bias and
can be about the same
for two types of estimates while both their bias and
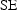 differ. It is very hard to
estimate the bias of an estimator unless the true parameter
value is, in fact, known. This is not true of the
differ. It is very hard to
estimate the bias of an estimator unless the true parameter
value is, in fact, known. This is not true of the
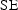 : the standard deviation of
the distribution of estimates of a parameter on replication
is the
: the standard deviation of
the distribution of estimates of a parameter on replication
is the  ; no knowledge of
the true value of the parameter is required. In many
situations, LS estimators of fixed effects parameters are
unbiased, although in nonlinear problems, such as most
pharmacokinetic ones, this cannot be assured.
; no knowledge of
the true value of the parameter is required. In many
situations, LS estimators of fixed effects parameters are
unbiased, although in nonlinear problems, such as most
pharmacokinetic ones, this cannot be assured. , which implicitly includes
, which implicitly includes
 ) and on the true parameter
values, including the variances (and covariances) of the
random effects influencing
) and on the true parameter
values, including the variances (and covariances) of the
random effects influencing 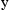 . If, for example, more observations were obtained in each
experiment (more individuals in a population study), the
spread of the estimates (one from each experiment) would
decrease until, in the limit, if an infinite number of
observations were obtained in each experiment, every
estimate would be the same (equal to the true value plus the
bias of the estimator). Thus, the distribution of the
estimate tells us nothing about biology or measurement
error, but only about the
. If, for example, more observations were obtained in each
experiment (more individuals in a population study), the
spread of the estimates (one from each experiment) would
decrease until, in the limit, if an infinite number of
observations were obtained in each experiment, every
estimate would be the same (equal to the true value plus the
bias of the estimator). Thus, the distribution of the
estimate tells us nothing about biology or measurement
error, but only about the  of the estimate itself.
of the estimate itself. and
and
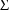 tell us about unexplained
(or random) interindividual variability (biology) or error
magnitude (biology plus measurement error), not about how
precisely we know these things. No matter how many
observations we make, interindividual variability will
remain the same size (but the variability of our estimate of
its size will decrease), as will the measurement error
variability of a particular instrument.
tell us about unexplained
(or random) interindividual variability (biology) or error
magnitude (biology plus measurement error), not about how
precisely we know these things. No matter how many
observations we make, interindividual variability will
remain the same size (but the variability of our estimate of
its size will decrease), as will the measurement error
variability of a particular instrument.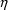 , say
, say
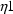 has a
has a
 ,
,
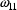 , while the estimate of
, while the estimate of
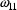 ,
,
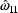 , also has a
, also has a
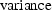 given by the square of the
standard error for
given by the square of the
standard error for 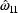 .
Indeed, the use of the term "standard error"
rather than "standard deviation" to name a measure
of the spread in the distribution of the parameter
.
Indeed, the use of the term "standard error"
rather than "standard deviation" to name a measure
of the spread in the distribution of the parameter
 rather than in the
parameter helps call attention to the distinction between
these two types of things.
rather than in the
parameter helps call attention to the distinction between
these two types of things. . In the
next sections we discuss three questions about such CIs a
little further. (i) How to estimate the
. In the
next sections we discuss three questions about such CIs a
little further. (i) How to estimate the
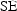 from a single set of data
(we cannot replicate our experiment many times and construct
a histogram as in figure 5.1). (ii) Given an estimate of
from a single set of data
(we cannot replicate our experiment many times and construct
a histogram as in figure 5.1). (ii) Given an estimate of
 , how to use that number
to compute a (95% confidence) interval with 95% chance of
containing the true parameter value. (iii) Given an estimate
of
, how to use that number
to compute a (95% confidence) interval with 95% chance of
containing the true parameter value. (iii) Given an estimate
of 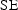 , how to compute a
confidence interval for a function of the
parameter.
, how to compute a
confidence interval for a function of the
parameter.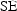 of a parameter estimate can be estimated using only the data
from a single experiment. The idea is that the data give us
estimates of the variances of all random effects in our
model, from which we can estimate the variability in future
data (if we were to replicate the experiment). That is, the
SE of the estimates on replication depends only on
quantities we either know or have estimates of: the
of a parameter estimate can be estimated using only the data
from a single experiment. The idea is that the data give us
estimates of the variances of all random effects in our
model, from which we can estimate the variability in future
data (if we were to replicate the experiment). That is, the
SE of the estimates on replication depends only on
quantities we either know or have estimates of: the
 , the number of
, the number of
 observed (
observed (
 ), and the variances of
all random effects.
), and the variances of
all random effects.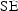 of a
parameter estimate; however, examples of how this can be
done are found in any statistical textbook on regression.
NONMEM presents the estimated standard error for each
parameter of the model (including the random effects
parameters,
of a
parameter estimate; however, examples of how this can be
done are found in any statistical textbook on regression.
NONMEM presents the estimated standard error for each
parameter of the model (including the random effects
parameters,  and
and
 ) as part of its
output.
) as part of its
output.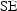 of a parameter
estimate, but also that for a LS estimate (and many other
kinds of estimates), the shape of the distribution of the
estimates is approximately Normal if the data set is large
enough. This means that we may use percentiles of the Normal
distribution, to compute confidence interval bounds (when
of a parameter
estimate, but also that for a LS estimate (and many other
kinds of estimates), the shape of the distribution of the
estimates is approximately Normal if the data set is large
enough. This means that we may use percentiles of the Normal
distribution, to compute confidence interval bounds (when
 is small, the
is small, the
 distribution is often used
instead; this is discussed in statistics texts). In general,
a 100(1-
distribution is often used
instead; this is discussed in statistics texts). In general,
a 100(1-  )% confidence
interval for a single parameter,
)% confidence
interval for a single parameter,
 say, is computed as
say, is computed as
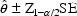 . Here
. Here
 denotes the
denotes the
 percentile of the Normal
distribution. As previously noted,
percentile of the Normal
distribution. As previously noted,
 is often chosen to be .05,
in which case
is often chosen to be .05,
in which case 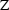 is
approximately 2.
is
approximately 2. of
a single parameter. If the lower and upper bounds of a
100(1-
of
a single parameter. If the lower and upper bounds of a
100(1-  )% confidence
interval for
)% confidence
interval for 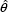 are denoted
are denoted
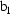 and
and
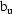 , respectively, then a
100(1-
, respectively, then a
100(1-  )% confidence
interval for
)% confidence
interval for 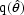 has lower and
upper bounds
has lower and
upper bounds 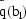 and
and
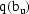 , respectively. This
confidence interval, however, is not necessarily centered at
, respectively. This
confidence interval, however, is not necessarily centered at
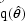 .
.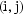 element of the matrix is the correlation between the ith and
jth parameter estimates. A large correlation (e.g.
element of the matrix is the correlation between the ith and
jth parameter estimates. A large correlation (e.g.
 ) means that the
conditional distribution of the ith estimate, given a fixed
value of the jth estimate, depends considerably on this
fixed value. Sometimes each parameter estimate of a pair
that is highly correlated has a large standard error,
meaning that neither parameter can be well-estimated. This
problem may be caused by data that do not distinguish among
the parameters very well, while a simpler model, or a
different design, or more data might permit more precise
estimates of each.
) means that the
conditional distribution of the ith estimate, given a fixed
value of the jth estimate, depends considerably on this
fixed value. Sometimes each parameter estimate of a pair
that is highly correlated has a large standard error,
meaning that neither parameter can be well-estimated. This
problem may be caused by data that do not distinguish among
the parameters very well, while a simpler model, or a
different design, or more data might permit more precise
estimates of each. : neither slope nor
intercept can be estimated at all as long as the other is
unknown, but fixing either one (simplifying the model)
determines the other. Both parameters could be estimated by
observing another point at some other value of
: neither slope nor
intercept can be estimated at all as long as the other is
unknown, but fixing either one (simplifying the model)
determines the other. Both parameters could be estimated by
observing another point at some other value of
 (more data), or, still
using just 2 points, by placing these points at two
different values of
(more data), or, still
using just 2 points, by placing these points at two
different values of  (modifying the design). Thus, when standard errors are
large, it is useful to examine the correlation matrix of
parameter estimates to see, in particular, if some
simplification of the model may help.
(modifying the design). Thus, when standard errors are
large, it is useful to examine the correlation matrix of
parameter estimates to see, in particular, if some
simplification of the model may help. and
and
 ). It uses the standard
errors of the parameter estimates and the correlations
between the parameter estimates. However, discussion of this
formula is beyond the scope of this introduction. If a
confidence interval for a function of several parameters is
desired, it is often more convenient to re-fit the data with
the model reparameterized to include the function as an
explicit parameter.
). It uses the standard
errors of the parameter estimates and the correlations
between the parameter estimates. However, discussion of this
formula is beyond the scope of this introduction. If a
confidence interval for a function of several parameters is
desired, it is often more convenient to re-fit the data with
the model reparameterized to include the function as an
explicit parameter.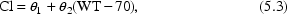
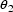 is close to zero, i.e.
that it is not so different from zero as to be clinically
significant. To make this precise, suppose that we know that
mean clearance for a 70 kg person (i.e.,
is close to zero, i.e.
that it is not so different from zero as to be clinically
significant. To make this precise, suppose that we know that
mean clearance for a 70 kg person (i.e.,
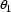 ) is about 100 ml/min. If
) is about 100 ml/min. If
 were .20 ml/min/kg or
less, a 50 kg increment (decrement) in weight from 70 kg
would be associated with less than a 10% change in total
clearance. This is clinically insignificant, so the
appropriate null values for
were .20 ml/min/kg or
less, a 50 kg increment (decrement) in weight from 70 kg
would be associated with less than a 10% change in total
clearance. This is clinically insignificant, so the
appropriate null values for
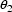 might be 0.0 to .20,
assuming, of course, that a physical lower bound for the
parameter is zero. (More usually in statistical discussions
a set of null values consists of a single number, e.g. 0.)
If the confidence interval for
might be 0.0 to .20,
assuming, of course, that a physical lower bound for the
parameter is zero. (More usually in statistical discussions
a set of null values consists of a single number, e.g. 0.)
If the confidence interval for
 only includes null values
(e.g., it is .10 to .15), one might then safely conclude
that weight, if it has any effect at all, has no
only includes null values
(e.g., it is .10 to .15), one might then safely conclude
that weight, if it has any effect at all, has no
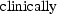 significant effect, and
that the data fully support the null hypothesis. If the
confidence interval includes null values and others (e.g.,
it is 0.0 to .60), one would conclude that there is some
support for the null hypothesis, but that there is also some
support for rejecting it. In this case the data are
insufficient to allow outright acceptance or rejection. If
the confidence interval includes no null values (e.g., it is
.80 to 1.3), one would reject the null hypothesis and
conclude that weight has a clinically significant (linear)
effect on clearance.
significant effect, and
that the data fully support the null hypothesis. If the
confidence interval includes null values and others (e.g.,
it is 0.0 to .60), one would conclude that there is some
support for the null hypothesis, but that there is also some
support for rejecting it. In this case the data are
insufficient to allow outright acceptance or rejection. If
the confidence interval includes no null values (e.g., it is
.80 to 1.3), one would reject the null hypothesis and
conclude that weight has a clinically significant (linear)
effect on clearance.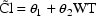

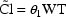
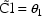
 to 0 produces the reduced
model, while in example #2, no parameter of the full model
can be fixed to a particular value to yield the
"reduced" model. It will always be true that if
the models are set up correctly, the number of parameters
that must be estimated will be greater in the full model
than in the reduced model. Note that this is not so for
example #2.
to 0 produces the reduced
model, while in example #2, no parameter of the full model
can be fixed to a particular value to yield the
"reduced" model. It will always be true that if
the models are set up correctly, the number of parameters
that must be estimated will be greater in the full model
than in the reduced model. Note that this is not so for
example #2.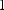 . If
NONMEM’s approximate model were the true model, then
. If
NONMEM’s approximate model were the true model, then
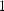 would be minus twice the
maximum logarithm of the likelihood of the data (for those
readers unfamiliar with likelihoods, and curious as to what
they are, we suggest consulting a statistics textbook).
Statistical theory tells us that the difference in minus
twice the maximum log likelihoods between a full and reduced
model can be referenced to a known distribution. Thus, to
perform the Likelihood Ratio Test, one proceeds as
follows.
would be minus twice the
maximum logarithm of the likelihood of the data (for those
readers unfamiliar with likelihoods, and curious as to what
they are, we suggest consulting a statistics textbook).
Statistical theory tells us that the difference in minus
twice the maximum log likelihoods between a full and reduced
model can be referenced to a known distribution. Thus, to
perform the Likelihood Ratio Test, one proceeds as
follows. be the
minimum value of the objective function from the fit to the
full model, and let
be the
minimum value of the objective function from the fit to the
full model, and let 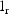 be the
corresponding quantity from the fit to the reduced model.
Fit both models separately yielding
be the
corresponding quantity from the fit to the reduced model.
Fit both models separately yielding
 and
and
 , and form the
statistic,
, and form the
statistic,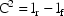
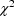 ) with
) with
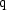 degree of freedom, where
degree of freedom, where
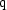 is the number of
parameters whose values are fixed in the reduced model. For
an
is the number of
parameters whose values are fixed in the reduced model. For
an  -level test, compare
-level test, compare
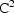 to
to
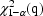 , the 100(1-
, the 100(1-
 ) percentile of the
) percentile of the
 distribution.
distribution. .
. were linear in the fixed
effects, then
were linear in the fixed
effects, then  would be
(approximately) distributed according to the
would be
(approximately) distributed according to the
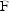 distribution with
distribution with
 , and
, and
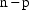 degrees of freedom (
degrees of freedom (
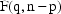 ). Since
). Since
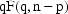 is equal to
is equal to
 only when
only when
 is "large", and
is greater otherwise, it is more conservative to reference
is "large", and
is greater otherwise, it is more conservative to reference
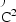 to
to
 in all instances, even
when
in all instances, even
when 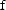 is
nonlinear.
is
nonlinear.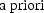 reason to prefer the
reduced model to the alternative, then the Likelihood Ratio
test can be used to test whether this a priori preference
must be rejected (at the
reason to prefer the
reduced model to the alternative, then the Likelihood Ratio
test can be used to test whether this a priori preference
must be rejected (at the  level). However, when one gives the matter some thought,
there is usually little objective reason to prefer
one model over another on a priori grounds. For example,
although possibly more convenient, a monoexponential model
is, if anything, less likely on biological grounds than a
biexponential.
level). However, when one gives the matter some thought,
there is usually little objective reason to prefer
one model over another on a priori grounds. For example,
although possibly more convenient, a monoexponential model
is, if anything, less likely on biological grounds than a
biexponential.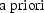 probability favoring one
contending model over another, but the two models may not
form a full and reduced model pair. In such circumstances,
one must rely on some goodness-of-fit criterion to
distinguish between the models. Consider choosing between
just two models (the ideas to be discussed readily
generalize to more than two), denoted model
probability favoring one
contending model over another, but the two models may not
form a full and reduced model pair. In such circumstances,
one must rely on some goodness-of-fit criterion to
distinguish between the models. Consider choosing between
just two models (the ideas to be discussed readily
generalize to more than two), denoted model
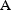 and model
and model
 . If the number of free
parameters in model
. If the number of free
parameters in model 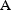 (
(
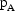 ) is the same as that of
) is the same as that of
 (
(
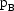 ), then here is a
reasonable criterion: favor the model with the better fit.
Note that there is no
), then here is a
reasonable criterion: favor the model with the better fit.
Note that there is no  value associated with this statement; no hypothesis is being
tested.
value associated with this statement; no hypothesis is being
tested.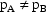 one cannot simply compare
one cannot simply compare
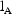 and
and
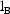 and choose the one with
the smaller value. The reason is best understood when
and choose the one with
the smaller value. The reason is best understood when
 and
and
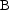 are a full and reduced
model pair. The full model will always fit the data
better (i.e., have a smaller
are a full and reduced
model pair. The full model will always fit the data
better (i.e., have a smaller
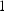 ) as it has more free
parameters to adjust its shape to the data. While the same
is not always true for any pair of non-linear models with
different numbers of parameters, it is often true: the model
with the greater number of parameters will fit a given data
set better than the model with fewer parameters. Yet the
larger (more parameters) model may not really be better; it
may, in fact, fit an entirely new data set worse than the
simpler model if its better fit to the original data was
simply because it exploited the flexibility of its extra
parameter(s) to better fit some random aspect of that
data.
) as it has more free
parameters to adjust its shape to the data. While the same
is not always true for any pair of non-linear models with
different numbers of parameters, it is often true: the model
with the greater number of parameters will fit a given data
set better than the model with fewer parameters. Yet the
larger (more parameters) model may not really be better; it
may, in fact, fit an entirely new data set worse than the
simpler model if its better fit to the original data was
simply because it exploited the flexibility of its extra
parameter(s) to better fit some random aspect of that
data. +
+
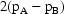 , and choose model
, and choose model
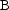 if
if
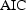 is >0, and model
is >0, and model
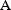 if
if
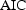 is <0. The second term
penalizes model
is <0. The second term
penalizes model 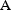 if
if
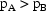 , and vice versa. When
, and vice versa. When
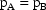 , the
, the
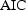 reduces to the comparison
of
reduces to the comparison
of 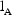 and
and
 described
previously.
described
previously.