NONMEM Users Guide Part VI - PREDPP - Chapter I
I. Overview of PREDPP
NONMEM Users Guide Part VI - PREDPP - Chapter I
I. Overview of PREDPP
PRED is a NONMEM subroutine that needs to be
supplied by the user. Its basic function is to compute
model-based predictions for observations. A PRED for
population pharmacokinetic data analysis can be very
complicated and difficult to write, and the NONMEM Project
Group has tried to help by writing PREDPP, a general version
of this subroutine that is particularly suited for the
analysis of population pharmacokinetic data. This version of
PRED is informally called PREDPP -- for PRED
Population Pharmacokinetics, but the formal name
of the subroutine is simply PRED, since this is the entry
name used by the calling programs in NONMEM. PREDPP can also
be used with NONMEM to analyze pharmacokinetic data from a
single subject, because the required predictions are of a
similar nature, and it can be used with NONMEM to
simulate either population or single-subject
pharmacokinetic data. As the reader shall see, PREDPP is a
very powerful tool for computing
pharmacokinetics.
There are a number of different basic kinetic
models that can be invoked by PREDPP. The user selects the
basic model by selecting one or more subroutines from a
library of subroutines of PREDPP and linking the selected
subroutines with the NONMEM and PREDPP subroutines that must
always be present in a load module. This process is
described in detail in chapter VII. The library is called
the PREDPP Library
For example: If the user is interested in a one
compartment linear model, he chooses subroutine ADVAN1 from
a list of PREDPP Library subroutines: ADVAN1, ADVAN2,
ADVAN3, etc., which, though distinguishable by the different
models they compute and by their informal names as just
stated, actually have the same formal name, ADVAN, since
this is the entry name used by the calling program in
PREDPP.
In addition to the one compartment model, other
kinetic models may be selected:
|
•
|
|
The one compartment linear model with first order
absorption from a drug depot compartment
[ADVAN2]
|
|
•
|
|
The two compartment linear mammillary model
[ADVAN3]
|
|
•
|
|
The two compartment linear mammillary model with
first order absorption from a drug depot compartment
[ADVAN4]
|
|
•
|
|
One of several general linear compartmental
models [ADVAN5,7]
|
|
•
|
|
One of several general nonlinear compartmental
models [ADVAN6,8,9]
|
|
•
|
|
The one compartment model with Michaelis-Menten
elimination [ADVAN10]
|
As will be discussed momentarily, this list
covers a good deal more than appears to be covered at first
glance. First, though, the distinction between a general
linear and a general nonlinear compartmental model is
clarified. A general linear compartmental model describes
linear kinetics with up to nine compartments, and the
computational algorithm employed is based on use of the
matrix exponential. Linear systems with only real
eigenvalues, or with possibly complex eigenvalues, are
reliably handled. A general nonlinear model describes either
linear or nonlinear kinetics with up to nine compartments,
and the computational algorithm employed is based on a
differential equation solver.
Most often with population pharmacokinetic data
analysis, a one or two compartment model suffices. Although
these models can also be implemented with a general linear
or nonlinear model, the specific implementations that have
been written for PREDPP are based on the traditional sums of
exponential forms, and are therefore computationally very
much faster than are implementations with the general
models.
With any of the models, a peripheral output
compartment is always present. Associated with this
compartment is a dimensionless pharmacokinetic parameter,
 . Of the entire amount,
. Of the entire amount,
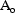 , of drug introduced into the
system and eliminated from it, a fraction
, of drug introduced into the
system and eliminated from it, a fraction
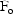 of this amount goes into this
output compartment. The output compartment may be turned on
and off; while on, drug accumulates therein, and when turned
off, the amount therein is reset to zero. So, for example,
if the output compartment is regarded as a urine compartment
(so
of this amount goes into this
output compartment. The output compartment may be turned on
and off; while on, drug accumulates therein, and when turned
off, the amount therein is reset to zero. So, for example,
if the output compartment is regarded as a urine compartment
(so 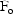 might be the ratio of
renal to total clearance), the initiation and termination of
a urine collection can be simulated. Alternatively, using
general linear or nonlinear models, compartments from which
no distribution can occur into any other compartments can be
defined within the system itself. Such compartments may also
be turned on and off.
might be the ratio of
renal to total clearance), the initiation and termination of
a urine collection can be simulated. Alternatively, using
general linear or nonlinear models, compartments from which
no distribution can occur into any other compartments can be
defined within the system itself. Such compartments may also
be turned on and off.
The kinetics, i.e. drug amounts, described by any
of these models can be parameterized by either
microconstants, i.e. rate constants, or certain
reparameterizations of the microconstants, possibly
involving other parameters such as volume of distribution.
The value of a kinetic parameter can depend in turn on the
values of physiological and other concomitant variables. For
any individual, the values of these concomitant variables
can change at discrete times, and so, therefore, can the
value of the PK parameter.
Drug can be input into any of the compartments
(except the output compartment) at any time. Bolus doses can
be given. In the case of the one compartment model with
first order absorption, for example, an IV bolus dose can be
input into the central compartment, and another oral bolus
dose can be input into the drug depot compartment at the
same or different time as the first dose is input. Also,
infusions of known amount and duration can be given. Also, a
bolus dose of a known amount can be given whose appearance
into a specified dose compartment, rather than being
instantaneous, is actually governed by a zero-order process,
the rate or time-duration of which may be regarded as a
kinetic parameter whose value may be specified or estimated.
So for example, a bolus dose in the form of a tablet may be
placed in a compartment, but due to the dissolution process,
its appearance in the compartment may be better described by
a zero-order process.
If many doses are given over time, as may happen
in a clinical setting, the specification of this in the data
record structure can be tedious, and the computation time is
affected since a state vector is updated at each time point
that a dose is given. If, however, these doses are given in
a regular cyclic fashion (e.g. 5 mg at 8 AM, 1 mg at 8 PM;
daily) and over such a sufficiently long time that the
system can be regarded as being at steady-state at the times
the doses of some particular cycle, i.e. the
"steady-state cycle", are given, then steady-state
kinetics can be used to greatly mitigate the dose
specification and computation time problems. Only the
steady-state cycle of doses need be specified, and the state
vector will only need to be updated at the times these doses
are given. Steady-state kinetics may be invoked for this
purpose with any of the PREDPP models (except with a general
nonlinear compartmental model when the nonlinear kinetics
imply that steady-state cannot be achieved).
If several doses are given over time, but they do
not lead to a steady-state, the specification of this in the
data record structure might still be tedious. However, if
these doses are the same type of dose, given with a constant
interdose interval, then in this case there is still a
convenient way to mitgate the specification
problem.
All the kinetic models are augmented by the
ability to allow any dose to appear in the system at some
lag time (called an absorption lag time) after the time the
dose is nominally given. All kinetic models are augmented by
the ability to allow a fraction (called a bioavailability
fraction) of any dose to appear in the system, rather than
the nominal dose. Absorption lag times and bioavailability
fractions may be specified or estimated.
Not only must PRED compute model based
predictions, it must also compute partial derivatives of the
statistical model for the observations with respect to all
random variables occurring in the model (see Guide I). This
computation has proved to be a particularly difficult one
for many users to program. Just as PREDPP serves the
important purpose of greatly simplifying the programming the
user must undertake to compute complicated population-type
pharmacokinetic predictions, it also serves the important
purpose of greatly simplifying the user-required programming
of the derivative computation for population pharmacokinetic
models.
The user must still be concerned with generating
a small amount of code in the form of two user-supplied
subroutines of PREDPP. The first routine, PK, functions
essentially to compute the values of pharmacokinetic
parameters, e.g. clearance, in terms of the values of
covariables, e.g. age and weight, and the values of random
interindividual effects accounting for random
interindividual variability. The second routine, ERROR,
functions essentially to specify the residual error
structure, e.g. to specify that residual error is additive,
or that it is multiplicative. However, PREDPP allows
pharmacodynamics along with pharmacokinetics to be modeled,
and it does so by allowing pharmacodynamic models to be
specified in the ERROR routine. This may strike the user as
a strange design, which it is. The design for PREDPP allows
pharmacokinetic models to be specified conveniently, and
only as an "afterthought" does it allow the
specification of pharmacodynamic models. Detailed discussion
of PK and ERROR is to be found in chapters III and IV. A few
other user-supplied subroutines are at times required.
Detailed discussion of these is to be found in chapter VI.
In particular, use of a general nonlinear compartmental
model requires the user to supply code for the involved
differential equations, but as seen in section VI.C, this
need not be a hard task.
TOP
TABLE OF CONTENTS
NEXT CHAPTER ...
 . Of the entire amount,
. Of the entire amount,
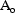 , of drug introduced into the
system and eliminated from it, a fraction
, of drug introduced into the
system and eliminated from it, a fraction
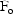 of this amount goes into this
output compartment. The output compartment may be turned on
and off; while on, drug accumulates therein, and when turned
off, the amount therein is reset to zero. So, for example,
if the output compartment is regarded as a urine compartment
(so
of this amount goes into this
output compartment. The output compartment may be turned on
and off; while on, drug accumulates therein, and when turned
off, the amount therein is reset to zero. So, for example,
if the output compartment is regarded as a urine compartment
(so 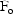 might be the ratio of
renal to total clearance), the initiation and termination of
a urine collection can be simulated. Alternatively, using
general linear or nonlinear models, compartments from which
no distribution can occur into any other compartments can be
defined within the system itself. Such compartments may also
be turned on and off.
might be the ratio of
renal to total clearance), the initiation and termination of
a urine collection can be simulated. Alternatively, using
general linear or nonlinear models, compartments from which
no distribution can occur into any other compartments can be
defined within the system itself. Such compartments may also
be turned on and off.