 of a PK parameter P
is
of a PK parameter P
isUser-supplied code is not needed to define the relationship between the pharmacokinetic parameters and the drug amounts in the various compartments (except when using a general nonlinear compartmental model; see section VI.C). This relationship is referred to as the kinetic relationship or the kinetics. As described in chapter I, these relationships are already coded into subroutines in the PREDPP Library. If, for example, a one-compartment linear model is to be used, ADVAN1 is chosen (see Chapter I). This subroutine computes drug amounts using, basically, the familiar monoexponential formula. However, user-supplied code for computing the values of the pharmacokinetic parameters themselves is needed. This code comprises a user-supplied subroutine called PK. This chapter is primarily concerned with a description of this routine.
To develop PK the user must first choose a set of pharmacokinetic parameters with which to describe the kinetics implemented by the chosen ADVAN routine. The kinetics can usually be described by several different sets of parameters. Having selected ADVAN1, for example, a user may choose to describe the kinetics in terms of the rate constant of elimination Ke, or he may prefer to describe them in terms of clearance and volume of distribution, Cl, and Vd. (In the first case Vd has to be modeled along with Ke if plasma concentrations are observed - but in order to scale drug amounts, not to compute them.) For each ADVAN, there exists a group of TRANS subroutines, TRANS1, TRANS2, TRANS3, etc., in the PREDPP Library. If Ke is chosen, the user chooses subroutine TRANS1 from the group for ADVAN1. If Cl and Vd are chosen, he chooses TRANS2. Each of these subroutines has the same formal name, TRANS, since this is the entry name that the calling program in PREDPP uses. The TRANS subroutine makes the translation between user-chosen pharmacokinetic parameters computed in PK and set of parameters used internally in the ADVAN subroutine. When, for example, an ADVAN is chosen which implements a linear kinetic model, the internal parameters are the rate constants, i.e. the microconstants, of the model. (With such an ADVAN, TRANS1 is a "dummy" translator that allows the user to compute the rate constants directly in PK.) The user could prefer to compute parameters for which no suitable translator is included in the Library, in which case he can either (i) include code in PK for the parameters he prefers, followed by code that performs the translation itself, and then use the dummy translator, or (ii) include code in PK for the parameters he prefers and then also supply his own TRANS subroutine. The requirements for supplying a user-written TRANS routine are addressed in section M.
Pharmacokinetic parameters are subject to interindividual variability, which must be taken into account by an appropriate statistical model. A more precise description of the PK routine is that it defines a statistical model for the PK parameters. A description of this model, and how it can be implemented by the PK routine, comprise the other sections of this chapter. Variability in the pharmacokinetic parameters that can be accounted for solely in terms of concomitant variables is addressed first in sections B and C. Unexplained variability that must be accounted for in terms of random individual effects is addressed second in sections D and E.
Values of pharmacokinetic (PK) parameters vary between individuals. This variability may be partially explained in terms of concomitant variables whose values vary between individuals. (The terms ’independent variable’ and ’covariable’ are also sometimes used.) The values of these variables may also vary within individuals over time; this particular situation is discussed in section B.2. Models for PK parameters that explain interindividual variability only in terms of concomitant variables are incomplete. Usually, there is evidence of variability in the PK parameters between individuals with the same set of values for the concomitant variables. This variability, unexplained by the concomitant variables, often appears as unexplained random variability, and may be modeled in terms of random individual effects, as discussed in section D below. As a result, the values of a PK parameter, between individuals with the same set, x, of values for the concomitant variables, will vary according to a probability distribution having a typical value (e.g. mean or geometric mean) depending on x. This value shall be called the typical value of the PK parameter for individuals whose concomitant values are those given by x. In section B.1 models for the relationship between the typical value of a PK parameter and the elements of x are discussed. (These models only involve the values of the concomitant variables.) An individual’s specific value of a PK parameter, in contrast to the typical value (for individuals with the same concomitant values), is called the subject-specific value
Models for subject-specific values are described in section D.
When all the data are from a single subject, this subject is regarded in isolation from other subjects, and the data are not what are commonly referred to as "population data". However, as a matter of NONMEM terminological convention, in this case the subject-specific value is also referred to as the typical value. The models described in this section for the typical value can be used as models for the subject-specific value (except that when there is more than one concomitant variable, there may be identifiabilty problems). Moreover, sections D and E are not applicable.
The issue of time-varying concomitant variables is discussed in section B.2. However, several important general concepts are also discussed in that section: state time, state-time interval, and continuous and discrete action of PK parameters.
The simplest model for the typical value
 of a PK parameter P
is
of a PK parameter P
is
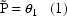
Namely, 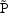 is a
constant, independent of x. Another model might
be
is a
constant, independent of x. Another model might
be

where WT is an individual’s weight. Here
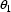 is a proportionality
constant. Model (2) might be used for
is a proportionality
constant. Model (2) might be used for
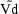 . In both (1) and (2),
. In both (1) and (2),
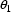 is a parameter which may be
estimated by NONMEM.
is a parameter which may be
estimated by NONMEM.
In order to model  it is helpful first, to model physiological variables in
terms of x, and second, to model
it is helpful first, to model physiological variables in
terms of x, and second, to model
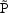 in terms of these
physiological variables. For example, let SIZE be a measure
of body size given by
in terms of these
physiological variables. For example, let SIZE be a measure
of body size given by

where HT is an individual’s height. Then,
perhaps, let  be given
by
be given
by

(If the data are from a single subject, and HT
and WT are not in fact time-varing, then
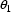 ,
,
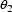 , and
, and
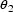 are not all identifiable.)
The physiological variable SIZE may be used also with models
for the typical values of other PK parameters, e.g.
metabolic clearance
are not all identifiable.)
The physiological variable SIZE may be used also with models
for the typical values of other PK parameters, e.g.
metabolic clearance

For another example, glomerular filtration rate may be modeled

where AGE and SCR are an individual’s age and serum creatinine measurement. Then the typical value of renal clearance may be given by

The typical value of total clearance could be given by

The model for  in
terms of physiological variables is often linear in the
in
terms of physiological variables is often linear in the
 ’s, as these examples
illustrate. The model for
’s, as these examples
illustrate. The model for  in
terms of x is often nonlinear in the
in
terms of x is often nonlinear in the
 ’s, as indicated by
(3) and (4) taken together.
’s, as indicated by
(3) and (4) taken together.
The discussion and examples in section B.1 apply when, for each individual, each concomitant variable has a single value. Essentially, the PK routine is called, and the typical value of a PK parameter is computed, using a model such as any of those described in section B.1. However, to a limited extent PREDPP also accommodates the case where the value x of the vector of concomitant variables varies within an individual over time. Again, the discussion and examples in section B.1 can apply, as is now described.
Note that a model for the typical value of a PK
parameter simply produces different typical values as x
varies. Similarly, as x varies, the subject-specific value
of the parameter (for a fixed value of
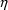 ; see the discussion in
section D) also varies. The value x can vary from event
record to event record (within an individual record), and if
the typical/subject-specific value is computed with each
event record, this allows the variation in the
typical/subject-specific value, across the time domain
during which observations are obtained, to be taken into
account, at least to within the time-resolution given by the
event times. To properly account for this variation, a fine
degree of time-resolution may be required. Event records can
be included in the individual record whose sole purpose is
to give values x at times of greater resolution (see section
V.B). If though, the concomitant variables are only measured
at certain discrete times, interpolated values may need to
be obtained for these "extra" event records. While
the interpolation per se can be implemented within the
NONMEM run (see section VI.A), the user must still include
extra event records in the data set which contain the extra
times. Also, PREDPP itself does not compute the interpolated
values, rather this computation must be completely specified
with user-supplied FORTRAN code.
; see the discussion in
section D) also varies. The value x can vary from event
record to event record (within an individual record), and if
the typical/subject-specific value is computed with each
event record, this allows the variation in the
typical/subject-specific value, across the time domain
during which observations are obtained, to be taken into
account, at least to within the time-resolution given by the
event times. To properly account for this variation, a fine
degree of time-resolution may be required. Event records can
be included in the individual record whose sole purpose is
to give values x at times of greater resolution (see section
V.B). If though, the concomitant variables are only measured
at certain discrete times, interpolated values may need to
be obtained for these "extra" event records. While
the interpolation per se can be implemented within the
NONMEM run (see section VI.A), the user must still include
extra event records in the data set which contain the extra
times. Also, PREDPP itself does not compute the interpolated
values, rather this computation must be completely specified
with user-supplied FORTRAN code.
The typical/subject-specific value can indeed be computed with each event record, or with a more limited set of event records if desired (see section H). It can even be computed with each event record and at certain additional times, allowing for just a bit more flexibility in obtaining interpolated values of the concomitant variables (see below and section H). How these computed values are used in the kinetic computations is outlined next.
The time domain is discretized at the event times, and at some other points as well. These times are called state times
and the time interval between two successive state times is called a state-time interval
The pharmacokinetic system, i.e. the state vector
of compartment amounts, is advanced from one state time to
the next, and the (typical and subject-specific) values of
the PK parameters are assumed to be constant over each
state-time interval (possibly different constants over each
interval). As the system is advanced, the routine PK is
called at various state times. When the system is advanced
over the state-time interval  , the PK routine will have already been called in order to
obtain the typical/subject-specific values of all the PK
parameters governing the kinetics over the interval. A more
precise description is given next.
, the PK routine will have already been called in order to
obtain the typical/subject-specific values of all the PK
parameters governing the kinetics over the interval. A more
precise description is given next.
A state time may be an event time, but there are other discrete times to which the system must be advanced, which are not (formally) event times. For example, an infusion may terminate at some time t, but while an infusion termination is not signalled by an event record, the system state changes in a discontinuous way at t. If time t is also an event time, it is only coincidental. Another example of a nonevent state time occurs when an absorption lag time is computed with a dose; the time the dose actually enters the system is a state time. This state time - indeed, any nonevent state time when either a bolus dose actually enters the system or when an infusion actually begins - is called a nonevent dose time
Of course, if the lag time is computed to be 0, then just coincidentally, the nonevent dose time is an event time, i.e. the time the dose was given. With any state time t there are associated one, or possibly two, particular event records. The first record is the one with event time t if t is itself an event time, or it is the first record whose event time follows t if t is not an event time. It is called the argument record associated with t, for a reason described in section C. If t is a nonevent dose time, then the event record describing the dose is also associated with t.
Certain PK parameters such as clearance act
continuously over state-time intervals in the sense that
drug amount in the system varies over such an interval
 according to a
pharmacokinetic model which depends on values of these
parameters at each instant in the interval. However, PREDPP
assumes that the (typical and subject-specific) values of
continuously acting PK parameters are constant over the
interval, and it obtains these constant values from a call
to PK where the argument record associated with
according to a
pharmacokinetic model which depends on values of these
parameters at each instant in the interval. However, PREDPP
assumes that the (typical and subject-specific) values of
continuously acting PK parameters are constant over the
interval, and it obtains these constant values from a call
to PK where the argument record associated with
 is made available to the
routine. The values of the concomitant variables on this
argument record determine the constant values of the PK
parameters holding over the interval (unless the PK routine
is written in such a way as to make use of information made
available to it from previous calls).
is made available to the
routine. The values of the concomitant variables on this
argument record determine the constant values of the PK
parameters holding over the interval (unless the PK routine
is written in such a way as to make use of information made
available to it from previous calls).
Other PK parameters such as a bioavailability fraction (see section F.2) act discretely at state times in the sense that drug amounts in the system vary from one state time to the next according to a pharmacokinetic model that depends on values of these parameters only at these times, although values of particular parameters are only needed at certain state times. In the case of a bioavailability fraction, for example (see section F.2), the model depends on the value of this parameter only at state times when doses enter (or start to enter) the system. For a nonevent dose time t, PREDPP normally obtains the values of these parameters from a call to PK with the argument record associated with t, and if requested, the event record describing the dose is also made available with this call. Information from one or both records may be needed to compute the values of a PK parameter such as bioavailability. For any other state time t, including all event times, PREDPP obtains the values from a call to PK with the argument record associated with t.
As concomitant values change across time, so does the information on event records, and then so does the output of the PK routine, i.e. the values of the kinetic parameters.
PK is a required user-supplied subroutine. Its first several statements, i.e. its preface
must be
SUBROUTINE PK (ICALL,IDEF,THETA,IREV,EVTREC,N,INDXS,IRGG,GG,NETAS) DIMENSION IDEF(7,*),THETA(*),EVTREC(IREV,*),INDXS(*),GG(IRGG,*) and if double precision NONMEM is used: DOUBLE PRECISION THETA,GG
When PK is called by PREDPP, it is passed values
for the vector  in THETA. It
is also passed a complete event record in EVTREC.
Specifically, EVTREC(I,J) contains the Jth data item of the
Ith data record of the event record. This record is the
argument record defined in the previous section. Its name
refers to the fact that it is passed to PK as a subroutine
argument, EVTREC. (As mentioned in section B.2, there are
circumstances where a dose record, different from the
argument record, may also be needed by the PK routine. A
description of how PK has access to this record is given in
section I.) PK is also passed the total number N of data
records comprising the event record. Typically N=1, and so
the first subscript of EVTREC will always be 1; however, see
chapter II.
in THETA. It
is also passed a complete event record in EVTREC.
Specifically, EVTREC(I,J) contains the Jth data item of the
Ith data record of the event record. This record is the
argument record defined in the previous section. Its name
refers to the fact that it is passed to PK as a subroutine
argument, EVTREC. (As mentioned in section B.2, there are
circumstances where a dose record, different from the
argument record, may also be needed by the PK routine. A
description of how PK has access to this record is given in
section I.) PK is also passed the total number N of data
records comprising the event record. Typically N=1, and so
the first subscript of EVTREC will always be 1; however, see
chapter II.
With these arguments the typical values of the PK
parameters may be computed. E.g. Let EVTREC(1,1) and
EVTREC(1,2) be height and weight, respectively. If
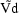 is given by (4) (of the
previous section), then one might use the code
is given by (4) (of the
previous section), then one might use the code
SIZE = EVTREC(1,1)**THETA(2)*EVTREC(1,2)**THETA(3) TVVD = THETA(1)*SIZE
This typical value of Vd will apply over any
state-time interval 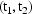 where
where
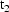 is a state time with which
the argument record is associated. When using the
first-order method of estimation, this typical value must be
communicated to PREDPP, as must the typical values of all
the PK parameters; the way to do this is discussed shortly.
(When conditional estimates are used, or simulation with
population data is implemented, subject-specific values must
be communicated instead; see section E.)
is a state time with which
the argument record is associated. When using the
first-order method of estimation, this typical value must be
communicated to PREDPP, as must the typical values of all
the PK parameters; the way to do this is discussed shortly.
(When conditional estimates are used, or simulation with
population data is implemented, subject-specific values must
be communicated instead; see section E.)
The one-dimensional array, INDXS, functions in a way similar to that of a larger array of the same name, described in Guide I, section C.4.1. In fact, INDXS is comprised of elements 12-50 of the larger array. The user places integers into that array, using the NONMEM control record INDEX (NM-TRAN control record $INDEX). These integers are then available to PREDPP and therefore to PK. The code.
I11 = INDXS(1) I12 = INDXS(2) I13 = INDXS(3) SIZE = EVTREC(I11,I12)**THETA(2)*EVTREC(I11,I13)**THETA(3) TVVD = THETA(1)*SIZE
has the same effect as has the previous code when INDXS(1), INDXS(2), and INDXS(3) are 1, 1, and 2, respectively. However, this code, unlike the previous code, frees the user from having to decide at the time PK is coded how the data items are going to be organized in the event record. PREDPP itself makes use of certain integers it requires be placed in elements 1-11 of the larger INDXS array (see section V.A), but it insures that INDXS(1), ..., INDXS(39), as made available to PK, refer to elements 12-50 of the larger array. So, the values 1, 1 and 2 of the example actually would be placed in elements 12-14 of that array.
With every translator routine, TRANS, there is associated a particular list of basic PK parameters whose values must be computed by PK, and a numbering of these parameters; see section VII.C. The parameters are numbered sequentially beginning with the number 1, but numbers may be skipped, e.g. 1,3,4,7. When the first-order method of estimation is used, the typical value of the Mth parameter should be placed in GG(M,1). So when, say, volume of distribution is numbered 2, before exiting, PK should execute code like this:
GG(2,1) = TVVD
The argument ICALL functions similarly to the ICALL argument described in Guide I, section C.4.2. It has 3 possible values when PK is called.
The value 1 signals to PK that the routine is being called for the first time in the NONMEM problem. At such a time PK must store certain information in array IDEF, but optionally, store certain information in GG. Here we discuss the matter concerning GG; the use of IDEF is discussed in sections G and H.
The value 2 signals to PK that the routine is being called in a regular fashion for data analytic purposes and that values of PK parameters are to be stored in the first column of GG. These can be typical values, as is described in this section, or they can be subject-specific values (see sections D and E). For data analytic purposes, however, it is not sufficient to compute values of PK parameters. Certain partial derivatives are also needed; see sections D and E.
The value 4 signals to PK that the routine is being called in a regular fashion for data simulation purposes. If the data are population data, (simulated) subject-specific values of PK parameters are to be stored in the first column of GG; see section E.2. If however, the data are all from a single subject, so that the subject’s specific values are synonomous with the typical values, then at ICALL=4 typical values are stored in this column.
At ICALL=1, 0’s and 1’s should be stored in the first column of GG. Usually, a 0 should be stored in GG(M,1), indicating that the user acknowledges that when ICALL=2 (or 4), the typical (or subject-specific) value of the Mth PK parameter will be placed in GG(M,1). When ICALL=1, the value passed to PK in GG(M,1) is 0; so if the user stores nothing in GG(M,1), he is achieving the same effect. If, though, a 1 is stored in GG(M,1), the user is specifying that when ICALL=2 (or 4), the (natural based) logarithm of the typical (or subject-specific) value of the Mth PK parameter will be placed in GG(M,1). PREDPP will exponentiate this logarithm so to obtain the typical (or subject-specific) value of the PK parameter. If this option is chosen, then at ICALL=2 the code for GG(2,1) might look like this:
ATVVD = LOG(THETA(1)*SIZE) GG(2,1) = ATVVD
which would be appropriate for model (4) and which would have the same effect as the above code, except that it would execute more slowly (because an extra logarithm and exponentiation are involved). Alternatively, the code for GG(2,1) might look like this:
ATVVD = LOG(THETA(1))+THETA(2)*LOG(EVTREC(2,1))
+THETA(3)*LOG(EVTREC(2,2))
GG(2,1) = ATVVD
which would also have the same effect as the above code, except that it would execute about as fast (because A**B is computed as EXP(B*LOG(A)).
The argument NETAS equals the total number of
user-defined  variables. The
user may possibly find this argument useful, particularly
for implementing models for subject-specific values of PK
parameters.
variables. The
user may possibly find this argument useful, particularly
for implementing models for subject-specific values of PK
parameters.
A model for subject-specific PK parameter values is needed for population data analysis and for the simulation of population data. Models for typical PK parameter values are discussed in section B, and their implementation in PREDPP is discussed in section C. If all the data come from the same subject, then the subject’s specific value of a PK parameter is simply his typical value, the discussions in sections B and C suffice, and the discussion in this section D is not applicable.
The typical value is to be associated with the subpopulation of individuals sharing the same set, x, of values for the concomitant variables. Any given individual of this subpopulation, though, has his own specific value of the PK parameter. Unexplainable interindividual variability refers to differences that exist between these subject-specific values. In this section models for subject-specific PK parameter values are discussed. Such a model gives the relationship between (a) a subject’s specific value of a PK parameter, and (b) the typical value for that (type of) subject and the random interindividual effects accounting for the difference between the subject’s specific value and his typical value. Also, as will be seen, with such a model concomitant variables may have an effect on (a) other than through the typical value.
Clearly, by accounting for the difference between the subject’s specific value and his typical value, across all subjects in the subpopulation, one also accounts for unexplainable interindividual variability. By doing so with random effects, this variability is modeled as arising randomly.
The simplest type model for an individual’s
specific value 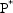 of a PK
parameter P is
of a PK
parameter P is

where 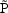 is the
typical value of P, but more specifically, the mean P in the
subpopulation of individuals whose concomitant values are
those given by x, and where
is the
typical value of P, but more specifically, the mean P in the
subpopulation of individuals whose concomitant values are
those given by x, and where 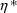 is the realization (i.e. value) of a random variable
is the realization (i.e. value) of a random variable
 with mean 0 and variance
with mean 0 and variance
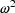 . The variable
. The variable
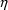 is a random effect
accounting for the unexplained interindividual variability
in P throughout the subpopulation; its realization
is a random effect
accounting for the unexplained interindividual variability
in P throughout the subpopulation; its realization
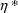 changes from individual to
individual. We shall henceforth omit the asterisk from a PK
parameter, P, when denoting an individual-specific value of
P, and also henceforth omit the asterisk from a random
variable such as
changes from individual to
individual. We shall henceforth omit the asterisk from a PK
parameter, P, when denoting an individual-specific value of
P, and also henceforth omit the asterisk from a random
variable such as 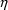 when
denoting an individual-specific realization of the variable.
Due to the context in which these symbols will be used
little problem should result from this ambiguity in
notation. Consequently, (9) may be rewritten
when
denoting an individual-specific realization of the variable.
Due to the context in which these symbols will be used
little problem should result from this ambiguity in
notation. Consequently, (9) may be rewritten

If 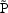 is given in
turn by (2), then we could write
is given in
turn by (2), then we could write

but for the purposes of what follows, it shall
not be necessary to expand 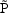 in terms of elements of x. However, we next describe how
in terms of elements of x. However, we next describe how
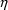 may in turn be further
modelled in terms of the elements of x, and so these
elements thus may appear explicitly in the final model for
P.
may in turn be further
modelled in terms of the elements of x, and so these
elements thus may appear explicitly in the final model for
P.
Actually,  may not
be entirely unexplainable. For example, it might be that
there are two groups of individuals, identifiable by some
dichotomous (0-1) valued concomitant variable, Z, say, and
that metabolic clearance may vary more widely in one group
than in the other, all other values of the concomitant
variables being equal. In other words, for some random
variable
may not
be entirely unexplainable. For example, it might be that
there are two groups of individuals, identifiable by some
dichotomous (0-1) valued concomitant variable, Z, say, and
that metabolic clearance may vary more widely in one group
than in the other, all other values of the concomitant
variables being equal. In other words, for some random
variable  with mean 0 and
variance
with mean 0 and
variance 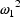 ,
,
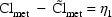



Written differently,

So 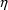 in (10) has
been expressed in terms of yet another random variable
in (10) has
been expressed in terms of yet another random variable
 . While
. While
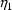 has homogeneous variance,
has homogeneous variance,
 does not; the variance of
does not; the variance of
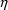 is
is
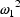 if Z=0 and
if Z=0 and
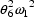 if Z=1. Note that parameters
like
if Z=1. Note that parameters
like 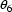 may enter the model for
may enter the model for
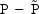 and may be
estimated.
and may be
estimated.
For the purposes of using NONMEM, the user should become familiar with expressing the model for P in terms of random variables with means 0 and homogeneous variances. So for example, (12) is preferred to
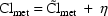
where 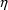 is the
variable with inhomogeneous variance considered
above.
is the
variable with inhomogeneous variance considered
above.
Another simple model for P is

where the mean and variance of
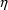 are 0 and
are 0 and
 , respectively. Here
, respectively. Here
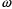 is the coefficient of
variation of P in the subpopulation. Instead of
is the coefficient of
variation of P in the subpopulation. Instead of
 having homogeneous variance
having homogeneous variance
 , perhaps
, perhaps
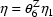 , as above. In any case,
under (13),
, as above. In any case,
under (13), 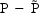 again can depend
on x, if only through
again can depend
on x, if only through 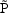 .
.
The random variables (with homogeneous variance)
occuring in a model for P may be regarded as having a
population meaning beyond the particular subpopulation
corresponding to x. They are independent of x. With every
individual sampled from the larger population, there are
associated with the individual (i) a particular set of
values for the concomitant variables (some of which, like a
dose, may be controlled by the investigator), and (ii) a
particular set of realizations of the random variables. The
variances of the random variables quantify random
interindividual variability in P in the larger population,
after the values of the concomitant variables are taken into
account. We think of the random variables (as we do with the
concomitant variables) as describing different population
effects (although, unlike the concomitant variables, these
effects are unobservable), and we think of their variances
as a kind of population parameter. These variances may be
estimated. The random effects confer the characteristics of
a random variable to P itself. With model (10), the standard
deviation of P is constant in the population if
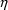 has homogeneous variance.
With model (13), the standard deviation of P in the
population is proportional to
has homogeneous variance.
With model (13), the standard deviation of P in the
population is proportional to
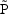 .
.
The mean and variance of a random variable are
suitable measures of centrality and dispersion,
respectively, if the distribution of the variable is
sufficiently Gaussian-like. Often the distribution of a PK
parameter P (for fixed x) is significantly right-skewed in
the population being sampled, and then the use of models
like (10) and (13), and the quantification of random
interindividual variability in terms of the variances of the
involved 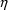 variables, are not
very appropriate. A more appropriate model might
be
variables, are not
very appropriate. A more appropriate model might
be

where the mean and variance of
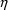 are 0 and
are 0 and
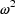 , respectively. This model
is, of course, equivalent to
, respectively. This model
is, of course, equivalent to

If the distribution of
 is Gaussian, then the
distribution of P is lognormal. In any case,
is Gaussian, then the
distribution of P is lognormal. In any case,
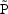 is the geometric mean of P,
and
is the geometric mean of P,
and 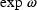 is the geometric
standard deviation of P. When
is the geometric
standard deviation of P. When
 is sufficiently small, and
is sufficiently small, and
 is Gaussian distributed, the
distribution of P itself is Gaussian-like, and model (13) is
not too bad an approximation to model (14). When
is Gaussian distributed, the
distribution of P itself is Gaussian-like, and model (13) is
not too bad an approximation to model (14). When
 is sufficiently small, the
mean and coefficient of variation of P are approximately
is sufficiently small, the
mean and coefficient of variation of P are approximately
 and
and
 , respectively.
, respectively.
If metabolic clearance and renal clearance are modeled by


then total clearance might be given by

This illustrates that a PK parameter might be
modeled in terms of more than one
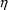 type variable. Also note
that (18) cannot be written equivalently in terms of
additive
type variable. Also note
that (18) cannot be written equivalently in terms of
additive  ’s, as in
(15), since the logarithm does not distribute over a
sum.
’s, as in
(15), since the logarithm does not distribute over a
sum.
In examples (10), (13), and (14),
 is obtainable from the model
for the subject-specific value of P by setting
is obtainable from the model
for the subject-specific value of P by setting
 to its mean value, 0 (the
typical value of
to its mean value, 0 (the
typical value of  ). By
analogy, a typical value for total clearance can be obtained
from (18) by setting both
). By
analogy, a typical value for total clearance can be obtained
from (18) by setting both 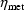 and
and  to 0,
yielding
to 0,
yielding

(see (8) of section B.1). However, this typical value is neither a mean nor geometric mean. A model for a subject-specific value of a PK parameter has been described in this section as being dependent on a model for a typical value. In general though, a model for a typical value can always be obtained from a model for a subject-specific value in the way just illustrated. In fact, when NONMEM/PREDPP needs a typical value, but a model for subject-specific values has been coded (see section E), the program will obtain the typical value in this way.
The reader should recognize that the
 variables discussed above
are the same type of
variables discussed above
are the same type of 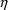 variables discussed in Guide I. Two such random effects can
correlate across individuals, and examples of this and the
way one can communicate this to NONMEM and obtain estimates
of covariability are described in that document.
variables discussed in Guide I. Two such random effects can
correlate across individuals, and examples of this and the
way one can communicate this to NONMEM and obtain estimates
of covariability are described in that document.
Conditional estimates of the
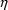 ’s used in the model
for a parameter P are obtained by searching for those values
for the
’s used in the model
for a parameter P are obtained by searching for those values
for the  ’s that
minimize a certain objective function. Values are tried
which vary somewhat independently of
’s that
minimize a certain objective function. Values are tried
which vary somewhat independently of
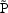 . So it is possible that
values of P result that are outside the meaningful range of
the parameter and at which meaningful kinetic predictions
are not computable. For example, if P is given by (13),
large enough negative values of
. So it is possible that
values of P result that are outside the meaningful range of
the parameter and at which meaningful kinetic predictions
are not computable. For example, if P is given by (13),
large enough negative values of
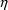 may be tried which produce
negative values of P, whereas P could be the volume of
distibution, for which negative values are meaningless. For
this reason, and because of the possiblility that the
distibution of P might be significantly right-skewed, a
model like (14) is often preferable when conditional
estimates are computed. (However, it may not be actually
necessary to use (14), and the more so P is symmetrically
distributed, the less of a problem it is to use
(13).)
may be tried which produce
negative values of P, whereas P could be the volume of
distibution, for which negative values are meaningless. For
this reason, and because of the possiblility that the
distibution of P might be significantly right-skewed, a
model like (14) is often preferable when conditional
estimates are computed. (However, it may not be actually
necessary to use (14), and the more so P is symmetrically
distributed, the less of a problem it is to use
(13).)
Estimates of the 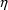 ’s do not result from using the first-order estimation
method. The only value of an
’s do not result from using the first-order estimation
method. The only value of an
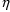 variable used with this
method is 0. As long as
variable used with this
method is 0. As long as  is
a meaningful value of P, the kinetic predictions are
computable. Therefore, from this point of view neither (13)
nor (14) is preferable when the first-order method is used.
Indeed, with first-order estimation models (13) and (14)
cannot be distinguished; see discussion below. Conceptually
though,
is
a meaningful value of P, the kinetic predictions are
computable. Therefore, from this point of view neither (13)
nor (14) is preferable when the first-order method is used.
Indeed, with first-order estimation models (13) and (14)
cannot be distinguished; see discussion below. Conceptually
though, 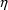 varies between
varies between
 and
and
 , even if the value 0 is
the only value used in the computation. So, strictly
speaking, model (13) can at best only be an approximate
statistical model for P.
, even if the value 0 is
the only value used in the computation. So, strictly
speaking, model (13) can at best only be an approximate
statistical model for P.
In fact, PREDPP checks that computed values of
certain PK parameters are meaningful, e.g. that
certain rate constants are positive, and if a value is not
meaningful, PREDPP avoids the computation of kinetic
predictions with this value and returns a PRED
error-recovery code to NONMEM so that NONMEM understands
that the "guilty" values of the
 ’s cannot serve as
estimates; see section K.1. (A check can be included in PK
itself, and an immediate return to NONMEM with a PRED
error-recovery code can be executed; see section K.2).
Often, this allows a model such as (13) to be used when
conditional estimates are computed; meaningful kinetic
predictions can always be computed and meaningful estimates
of the
’s cannot serve as
estimates; see section K.1. (A check can be included in PK
itself, and an immediate return to NONMEM with a PRED
error-recovery code can be executed; see section K.2).
Often, this allows a model such as (13) to be used when
conditional estimates are computed; meaningful kinetic
predictions can always be computed and meaningful estimates
of the  ’s can be
obtained. Nonetheless, when the distribution of P is
significantly right-skewed in the population, use of model
(14) can produce a better description of random
interindividual variability in P, and this may not be
detected when (13) is the only model tried and inherent
problems with using (13) are masked.
’s can be
obtained. Nonetheless, when the distribution of P is
significantly right-skewed in the population, use of model
(14) can produce a better description of random
interindividual variability in P, and this may not be
detected when (13) is the only model tried and inherent
problems with using (13) are masked.
When using a conditional estimation method, it is also possible for values of several parameters to result which are not meaningfully related. For example, suppose the kinetics are linear, one compartment with first-order absorption (ADVAN2), and that the elimination and absorption rate constants and the volume of distribution are given by

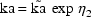
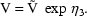
(Here V is needed as a scaling parameter (see
section F), not for the computation of compartment amounts.)
Then values of 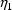 and
and
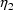 may be tried which produce
values
may be tried which produce
values 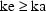 , whereas for the
drug in question, suppose only
, whereas for the
drug in question, suppose only
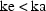 is meaningful. With these
values of
is meaningful. With these
values of  and
and
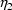 meaningful kinetic
predictions can be computed, but only if the roles of ke and
ka are reversed in the kinetic model. However, reversing
their roles entails reversing the roles of
meaningful kinetic
predictions can be computed, but only if the roles of ke and
ka are reversed in the kinetic model. However, reversing
their roles entails reversing the roles of
 and
and
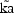 , and also of
, and also of
 and
and
 , and therefore, also of
, and therefore, also of
 and
and
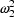 (as well as changing the
meanings of
(as well as changing the
meanings of  ,
,
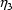 , and
, and
 ). The quantities
). The quantities
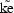 ,
,
 ,
,
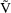 ,
,
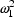 ,
,
 ,
,
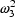 are population
quantities, applying to all individuals (with given x), and
fixed in value for the purpose of estimating the
are population
quantities, applying to all individuals (with given x), and
fixed in value for the purpose of estimating the
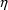 ’s. Changing their
meanings, so that the parameter values of ke, ka, and V are
meaningful for one individual, entails changing their
meanings as they apply to all individuals. Under such a
reinterpretation of these population quantities, and with
their given values, it is now possible that values of the
’s. Changing their
meanings, so that the parameter values of ke, ka, and V are
meaningful for one individual, entails changing their
meanings as they apply to all individuals. Under such a
reinterpretation of these population quantities, and with
their given values, it is now possible that values of the
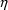 ’s for yet another
individual might be tried which give rise to nonmeaningful
values ke, ka, and V for him. So a problem remains. The
well-known parameter "flip-flop" phenomenon is not
handled as easily in population PK data analysis as it is in
single-subject PK data analysis.
’s for yet another
individual might be tried which give rise to nonmeaningful
values ke, ka, and V for him. So a problem remains. The
well-known parameter "flip-flop" phenomenon is not
handled as easily in population PK data analysis as it is in
single-subject PK data analysis.
When ADVAN2 is used, the user can check in PK
whether  , and if so, can
force PREDPP to avoid the computation of kinetic predictions
and return a PRED error-recovery code to NONMEM, so that
NONMEM understands that the "guilty" values of the
, and if so, can
force PREDPP to avoid the computation of kinetic predictions
and return a PRED error-recovery code to NONMEM, so that
NONMEM understands that the "guilty" values of the
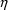 ’s cannot serve as
estimates (see section K.2). However again, a better
solution is to try another type of model involving
’s cannot serve as
estimates (see section K.2). However again, a better
solution is to try another type of model involving
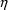 ’s, e.g.
’s, e.g.

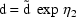

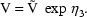
where constraints on
 ’s are used to ensure
that
’s are used to ensure
that  . This model
explicitly recognizes that
. This model
explicitly recognizes that  in the population. Therefore, it also implies that ke and ka
cannot be statistically independent (even if
in the population. Therefore, it also implies that ke and ka
cannot be statistically independent (even if
 and
and
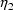 are assumed to be
independent). Model (20), with or without the assumption
that
are assumed to be
independent). Model (20), with or without the assumption
that 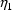 and
and
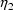 are independent, is at best
only an approximate statistical model for ke and
ka.
are independent, is at best
only an approximate statistical model for ke and
ka.
Generally speaking, the PK routine specifies a subject-specific model for (all) the PK parameters. It does this in different ways, depending on whether PREDPP is being called for the purposes of data analysis, or data simulation, or both, and depending on the estimation method being used. For the purposes of data simulation, the specification uses the type of mathematical expressions for subject-specific values shown above.
For the purposes of data analysis, the
specification can entail expressions for subject-specific
values, such as those shown above, or instead, it can entail
expressions for typical values. In either case, it also
always entails expressions for a set of first partial
derivatives of the model for the subject-specific values of
the PK parameters with respect to the
 ’s. For the purpose
of data analysis using the Laplacian method, the
specification further entails expressions for a set of
second-partial derivatives. The matter of first-partial
derivatives is addressed first.
’s. For the purpose
of data analysis using the Laplacian method, the
specification further entails expressions for a set of
second-partial derivatives. The matter of first-partial
derivatives is addressed first.
The first-partial derivatives of the model for
the subject-specific values of the PK parameters with
respect to the 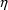 ’s, as
functions of the
’s, as
functions of the 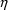 ’s,
are called the subject-specific first-partial
derivatives
’s,
are called the subject-specific first-partial
derivatives
For (12)-(14) and (18) for example, the first-partials are





These types of expressions are used whenever
conditional estimates are computed. They are also used when
the first-order estimation method is used, but then the
first-partials must be evaluated at all
 ’s equal 0. These
first-partial derivatives are called the typical
first-partial derivatives
’s equal 0. These
first-partial derivatives are called the typical
first-partial derivatives
For the above examples these are





Note that the derivatives (28) and (29) are
identical. With the first-order estimation method, the model
for subject-specific values of the PK parameters is fully
defined by specifying the typical values and the typical
first-partial derivatives. Since the typical values are the
same under models (13) and (14), and since the derivatives
(28) and (29) are also the same, the first-order estimation
method can never distinguish between models (13) and (14).
That is, the same fit will result from using either model.
In effect, an assumption is being made that the variance of
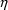 in (14) is small, and that
the mean and coefficient of variation of P under model (14)
are well approximated by
in (14) is small, and that
the mean and coefficient of variation of P under model (14)
are well approximated by 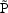 and
and  , respectively. With
the conditional estimation methods, however, the model for
subject-specific values of the PK parameters is defined by
specifying the subject-specific values themselves, along
with subject-specific partial derivatives. Since expressions
(13) and (14) differ for some values of
, respectively. With
the conditional estimation methods, however, the model for
subject-specific values of the PK parameters is defined by
specifying the subject-specific values themselves, along
with subject-specific partial derivatives. Since expressions
(13) and (14) differ for some values of
 , the population
conditional estimation methods can distinguish between
models (13) and (14) when the data allow this.
, the population
conditional estimation methods can distinguish between
models (13) and (14) when the data allow this.
It should be emphasized that the typical
first-partial derivatives, despite their name and the fact
that to obtain them all 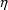 ’s are set to zero, convey information about the model
for subject-specific values. They are rates of change of PK
parameters with respect to interindividual
effects.
’s are set to zero, convey information about the model
for subject-specific values. They are rates of change of PK
parameters with respect to interindividual
effects.
As noted in section C, the PK routine allows a
model to be defined for  ,
rather than for P. The derivatives of
,
rather than for P. The derivatives of
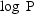 with respect to the
involved
with respect to the
involved 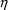 ’s, rather
than the derivatives of P itself, may be specified. The
subject-specific (and typical) first-partial derivative of
’s, rather
than the derivatives of P itself, may be specified. The
subject-specific (and typical) first-partial derivative of
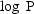 from (15), for example,
is
from (15), for example,
is

PREDPP transforms
 to
to
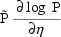 since it needs the
latter.
since it needs the
latter.
Just as typical values can always be obtained from expressions for subject-specific values, so can typical first-partials.
Second-partial derivatives are needed when the
Laplacian estimation method is used. The second-partial
derivatives of the model for the subject-specific values of
the PK parameters with respect to the
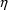 ’s, as functions of
the
’s, as functions of
the 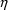 ’s, are called
the subject-specific second-partial
derivatives
’s, are called
the subject-specific second-partial
derivatives
These often are simply 0. For the above examples these are






The subject-specific second-partial derivative of
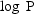 from (15) is
from (15) is

Second-partial derivatives of the model for the
subject-specific values of the PK parameters with respect to
the 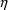 ’s, evaluated at
all
’s, evaluated at
all  ’s equal to 0
(i.e. typical second-partial derivatives) may, of course,
also be considered, but they are never needed in NONMEM
computations.
’s equal to 0
(i.e. typical second-partial derivatives) may, of course,
also be considered, but they are never needed in NONMEM
computations.
For the purpose of data analysis with population
data, models for the subject-specific values must be
communicated to PREDPP. When the first-order estimation
method is used, this involves communicating the typical
values of the PK parameters (see section C), and also the
typical first-partial derivatives, the implementation of
which is discussed in section E.1. When a conditional
estimation method is used, or posthoc estimates of
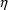 ’s are desired, this
involves communicating subject-specific PK parameter values
and subject-specific first-partial derivatives.
Implementation of the former is discussed in section E.2,
and implementation of the latter is discussed in section
E.3. Also the simulation of population data uses
subject-specific values of PK parameters. The Laplacian
method uses subject-specific second-partial derivatives, and
the implementation of these is discussed in section
E.4.
’s are desired, this
involves communicating subject-specific PK parameter values
and subject-specific first-partial derivatives.
Implementation of the former is discussed in section E.2,
and implementation of the latter is discussed in section
E.3. Also the simulation of population data uses
subject-specific values of PK parameters. The Laplacian
method uses subject-specific second-partial derivatives, and
the implementation of these is discussed in section
E.4.
The first-order method can also be used when
subject-specific values and subject-specific first-partial
derivatives are communicated. Implementation of this mode of
communication is generally preferable for the development of
new PK codes, for although one may intend to only use
the first-order method, one might actually end up needing to
compute conditional estimates (e.g. posthoc estimation of
 ’s).
’s).
When all the data come from a single subject, both subject-specific values and derivatives are irrelevant, and this section is not applicable. For the purpose of reading this section the reader should be familiar with section C.
If the first-order estimation method is used,
typical first-partial derivatives must be computed (see
section D). The 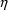 ’s
involved in the models for the subject-specific values of
the PK parameters are numbered according to the enumeration
of the initial estimates of their variances in NONMEM (or
NM-TRAN) control records. The derivative of the Mth PK
parameter with respect to
’s
involved in the models for the subject-specific values of
the PK parameters are numbered according to the enumeration
of the initial estimates of their variances in NONMEM (or
NM-TRAN) control records. The derivative of the Mth PK
parameter with respect to  should be placed in GG(M,1+K). (The Mth PK parameter is
defined in section C.) So if (total) clearance is the lst PK
parameter and is given by (18), and if
should be placed in GG(M,1+K). (The Mth PK parameter is
defined in section C.) So if (total) clearance is the lst PK
parameter and is given by (18), and if
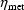 and
and
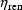 are the 4th and 5th
are the 4th and 5th
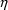 variables, respectively,
then one needs code like
variables, respectively,
then one needs code like
GG(1,1) = TVCLMT+TVCLRN ...
GG(1,5) = TVCLMT GG(1,6) = TVCLRN
(see section D equations (19),(30),(31)).
All values GG(1,1+K),
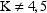 , should be 0. However,
since whenever PK is called, the GG array is initialized to
zero immediately before the call, the user need not
explicitly store zeros in elements of GG.
, should be 0. However,
since whenever PK is called, the GG array is initialized to
zero immediately before the call, the user need not
explicitly store zeros in elements of GG.
By storing a 1 in GG(M,1) at ICALL=1, the user
specifies that when ICALL=2, the typical value of the
logarithm of the Mth PK parameter will be placed in GG(M,1)
(see section C). This signal also means that the typical
first derivative of the logarithm of the Mth PK parameter
with respect to  will be
placed in GG(M,K+1). To take an example, if
will be
placed in GG(M,K+1). To take an example, if
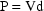 is the 2nd PK parameter, if
is the 2nd PK parameter, if
 is given by (15), and if
is given by (15), and if
 in (15) is the 1st
in (15) is the 1st
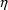 variable, then one needs
code like
variable, then one needs
code like
GG(2,1) = ATVVD GG(2,2) = 1
See section C for examples of ATVVD. In this example when ICALL=1, one also needs GG(2,1)=1.
When ICALL=4, PK is being called during the Simulation Step, and then subject-specific values must be computed. When ICALL=2, PK is being called for the purpose of data analysis, and when conditional estimates are involved, then too, subject-specific values must be computed. When the first-order estimation method is used, it suffices to compute subject-specific values, since typical values can always be obtained from subject-specific computations (section D).
Subject-specific values are stored in the first
column of the GG array, as are typical values when they are
stored; see section C. However again, since typical values
can always be obtained from subject-specific value
computations, subject-specific values may be computed and
stored in the first column whenever both types of values may
be needed. As an example, when both simulation and data
analysis using the first-order estimation method occur in
the same run, subject-specific values should be computed and
stored. Or, when a run involves posthoc estimation of
 ’s, subject-specific
values should be computed and stored. As a final example,
when a run involves two problems, one using the first-order
method, and another using a conditional method,
subject-specific values should be computed and
stored.
’s, subject-specific
values should be computed and stored. As a final example,
when a run involves two problems, one using the first-order
method, and another using a conditional method,
subject-specific values should be computed and
stored.
The subject-specific value of the Mth parameter
is stored in GG(M,1). So if (total) clearance is the lst PK
parameter and is given by (18), and if
 and
and
 are the 4th and 5th
are the 4th and 5th
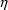 variables, respectively,
then one needs code like
variables, respectively,
then one needs code like
DIMENSION ETA(6) DOUBLE PRECISION ETA ...
CALL GETETA (ETA)
...
GG(1,1) = TVCLMT*EXP(ETA(4))+TVCLRN*EXP(ETA(5))
ETA is a one-dimensional array used to store
values of  ,
,
 ,
,
 , needed for the
computation of subject-specific values of the PK parameters.
Its dimension should be no less than the actual number of
, needed for the
computation of subject-specific values of the PK parameters.
Its dimension should be no less than the actual number of
 ’s being used, and it
should be declared DOUBLE PRECISION when Double Precision
NONMEM is used. When ICALL=4, the values of
’s being used, and it
should be declared DOUBLE PRECISION when Double Precision
NONMEM is used. When ICALL=4, the values of
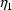 ,
,
 ,
,
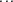 are obtained by a call to
the NONMEM utility routine SIMETA. An example of the use of
SIMETA is given in section L.1. When ICALL=2, these values
are obtained by a call to the NONMEM utility routine
GETETA.
are obtained by a call to
the NONMEM utility routine SIMETA. An example of the use of
SIMETA is given in section L.1. When ICALL=2, these values
are obtained by a call to the NONMEM utility routine
GETETA.
If the NONMEM run is only for the purpose of
simulation, a simple call to SIMETA at ICALL=4, preceding
the first reference to ETA in an executable statement,
suffices to obtain the  values. If the NONMEM run does not involve simulation, a
simple call to GETETA at ICALL=2, preceding the first
reference to ETA in an executable statement, suffices to
obtain the
values. If the NONMEM run does not involve simulation, a
simple call to GETETA at ICALL=2, preceding the first
reference to ETA in an executable statement, suffices to
obtain the 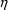 values, as in
the above example. However, a run could entail calls to PK
with values of ICALL=2 and 4. Or, the user might prefer that
PK be coded to allow such a possiblity in a future run using
the PK routine. In this case the following type of code can
be written.
values, as in
the above example. However, a run could entail calls to PK
with values of ICALL=2 and 4. Or, the user might prefer that
PK be coded to allow such a possiblity in a future run using
the PK routine. In this case the following type of code can
be written.
DIMENSION ETA(6) DOUBLE PRECISION ETA ...
IF (ICALL.EQ.4) CALL SIMETA (ETA) IF (ICALL.EQ.2) CALL GETETA (ETA)
...
GG(1,1) = TVCLMT*EXP(ETA(4))+TVCLRN*EXP(ETA(5))
Lastly, GETETA must always be initialized at ICALL=1. This involves simply calling GETETA at ICALL=1. So, the code actually might look like:
DIMENSION ETA(6) DOUBLE PRECISION ETA ...
IF (ICALL.EQ.1) THEN
... CALL GETETA (ETA) ... RETURN
ENDIF
...
IF (ICALL.EQ.4) CALL SIMETA (ETA) IF (ICALL.EQ.2) CALL GETETA (ETA)
...
GG(1,1) = TVCLMT*EXP(ETA(4))+TVCLRN*EXP(ETA(5))
The initialization call does not result in values
of 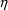 ’s being stored in
ETA. Only calls to GETETA at ICALL=2 or 4 result in
’s being stored in
ETA. Only calls to GETETA at ICALL=2 or 4 result in
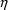 ’s being stored.
Often initialization of GETETA is not the only task that is
undertaken at ICALL=1; see sections G and H.
’s being stored.
Often initialization of GETETA is not the only task that is
undertaken at ICALL=1; see sections G and H.
As stated earlier in this section, when the first-order method is used, and when the only values of PK parameters that are needed are typical values, expressions for subject-specific values may be coded instead. When the first-order method is used, GETETA stores zeros in ETA, and then the subject-specific values become the required typical values.
By storing a 1 in GG(M,1) at ICALL=1, the user specifies that when ICALL=2 or 4, the subject-specific value of the logarithm of the Mth PK parameter will be placed in GG(M,1) (see section C).
Something further about simulation: By default,
as long as PK is being called with an event record from the
same individual record, each time SIMETA is called, the
values 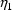 ,
,
 ,
,
 stored in ETA remain the
same; there is only one set of values obtained for the
individual. However, the simulation can be done in such a
way that the values change each time SIMETA is called (see
Guide IV, section III.B.13). Then only the first time PK
itself is called with an event record of a given individual
record should PK call SIMETA (see section H for a discussion
about the sequence of calls to PK). This assures that there
is only one set of values obtained for the individual, as in
the default situation. Unlike that situation, though, during
this first call to PK, multiple calls to SIMETA might occur.
So for example, simulated values of
stored in ETA remain the
same; there is only one set of values obtained for the
individual. However, the simulation can be done in such a
way that the values change each time SIMETA is called (see
Guide IV, section III.B.13). Then only the first time PK
itself is called with an event record of a given individual
record should PK call SIMETA (see section H for a discussion
about the sequence of calls to PK). This assures that there
is only one set of values obtained for the individual, as in
the default situation. Unlike that situation, though, during
this first call to PK, multiple calls to SIMETA might occur.
So for example, simulated values of
 , obtained from multiple
calls to SIMETA and such that
, obtained from multiple
calls to SIMETA and such that
 , can be rejected until a
value
, can be rejected until a
value  is obtained, i.e. the
distribution on
is obtained, i.e. the
distribution on  can be
truncated. The code might look like this:
can be
truncated. The code might look like this:
DIMENSION ETA(6)
DOUBLE PRECISION ETA
...
IF (ICALL.EQ.1) THEN
...
CALL GETETA (ETA)
...
RETURN
ENDIF
...
IF (ICALL.EQ.4) THEN
IF (NEWIND.NE.2) THEN
5 CALL SIMETA (ETA)
IF (ABS(ETA(1)).GE.2.) GO TO 5
ENDIF
ENDIF
IF (ICALL.EQ.2) CALL GETETA (ETA)
...
GG(1,1) = TVCLMT*EXP(ETA(4))+TVCLRN*EXP(ETA(5))
The variable NEWIND allows PK to know when it is being called for the first time with an event record of a given individual record (i.e. NEWIND not equal to 2); see section I.
For the purpose of data analysis, routine PK is
called with ICALL=2, at which time derivatives must be
computed. If a conditional estimation method is used or
posthoc estimates of the  ’s are desired, subject-specific first-partial
derivatives must be computed (see section D). If the
Laplacian method is used, subject-specific second-partial
derivatives must also be computed; see section
E.4.
’s are desired, subject-specific first-partial
derivatives must be computed (see section D). If the
Laplacian method is used, subject-specific second-partial
derivatives must also be computed; see section
E.4.
The  ’s
involved in the models for the subject-specific values of
the PK parameters are numbered according to the enumeration
of the initial estimates of their variances in NONMEM (or
NM-TRAN) control records. The derivative of the Mth PK
parameter with respect to
’s
involved in the models for the subject-specific values of
the PK parameters are numbered according to the enumeration
of the initial estimates of their variances in NONMEM (or
NM-TRAN) control records. The derivative of the Mth PK
parameter with respect to  should be placed in GG(M,1+K). (The Mth PK parameter is
defined in section C) So if (total) clearance is the lst PK
parameter and is given by (18), and if
should be placed in GG(M,1+K). (The Mth PK parameter is
defined in section C) So if (total) clearance is the lst PK
parameter and is given by (18), and if
 and
and
 are the 4th and 5th
are the 4th and 5th
 variables, respectively,
then one needs code like
variables, respectively,
then one needs code like
DIMENSION ETA(6) DOUBLE PRECISION ETA ...
IF (ICALL.EQ.1) THEN
... CALL GETETA (ETA) ... RETURN
ENDIF
...
CALL GETETA (ETA)
...
GG(1,1) = TVCLMT*EXP(ETA(4))+TVCLRN*EXP(ETA(5)) GG(1,5) = TVCLMT*EXP(ETA(4)) GG(1,6) = TVCLRN*EXP(ETA(5))
All values GG(1,1+K),
 , should be 0. However,
since whenever PK is called, the GG array is initialized to
zero immediately before the call, the user need not
explicitly store zeros in elements of GG.
, should be 0. However,
since whenever PK is called, the GG array is initialized to
zero immediately before the call, the user need not
explicitly store zeros in elements of GG.
By storing a 1 in GG(M,1) at ICALL=1, the user
specifies that when ICALL=2 or 4, the subject-specific value
of the logarithm of the Mth PK parameter will be placed in
GG(M,1) (see section C). This signal also means that the
subject-specific first derivative of the logarithm of the
Mth PK parameter with respect to
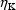 will be placed in
GG(M,K+1).
will be placed in
GG(M,K+1).
If the Laplacian estimation method is used, subject-specific first and second-partial derivatives are required (see section D). The second-partial derivatives should be computed when ICALL=2. If one might use the Laplacian method, then it is a good idea to develop a PK code that accommodates this. If the Laplacian method is not used and the second-partial derivatives are computed, then they are ignored. See also the remarks below concerning MSEC.
When second-partial derivatives are computed, the
GG argument is dimensioned differently from the way this is
described in section C. Its dimension needs to be expressed
thusly: GG(IRGG,11,*) The subject-specific value of the Mth
PK parameter should be placed in GG(M,1,1). The
first-partial derivative of the Mth PK parameter with
respect to 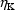 should be placed
in GG(M,1+K,1). The second-partial derivative of the Mth PK
parameter with respect to
should be placed
in GG(M,1+K,1). The second-partial derivative of the Mth PK
parameter with respect to  and
and  should be placed in
GG(M,1+K,1+L). The matrix of second-partial derivatives is
symmetric, so it is only necessary to store second-partial
derivatives for values
should be placed in
GG(M,1+K,1+L). The matrix of second-partial derivatives is
symmetric, so it is only necessary to store second-partial
derivatives for values  .
Consider the example where (total) clearance is the lst PK
parameter and is given by (18), and
.
Consider the example where (total) clearance is the lst PK
parameter and is given by (18), and
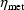 and
and
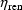 are the 4th and 5th
are the 4th and 5th
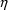 variables, respectively.
Then one needs code like
variables, respectively.
Then one needs code like
DIMENSION ETA(6) DOUBLE PRECISION ETA ...
IF (ICALL.EQ.1) THEN
... CALL GETETA (ETA) ... RETURN
ENDIF
...
CALL GETETA (ETA)
...
GG(1,1,1) = TVCLMT*EXP(ETA(4))+TVCLRN*EXP(ETA(5)) GG(1,5,1) = TVCLMT*EXP(ETA(4)) GG(1,6,1) = TVCLRN*EXP(ETA(5)) GG(1,5,5) = GG(1,5,1) GG(1,6,6) = GG(1,6,1)
All values GG(1,1+K,1+L),
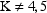 , should be 0. However,
since whenever PK is called, the GG array is initialized to
zero immediately before the call, the user need not
explicitly store zeros in elements of GG.
, should be 0. However,
since whenever PK is called, the GG array is initialized to
zero immediately before the call, the user need not
explicitly store zeros in elements of GG.
In the above example, there are only two nonzero second-partial derivatives of clearance that must be explictly stored in GG. However, even these two are not actually needed with every call to PK. (Certainly, they are never needed unless the Laplacian method is being used.) In order to save computation time, information is provided in the NONMEM read-only common ROCM12 as to whether second-partial derivatives are needed with a particular call to PK. This is particularly useful when there are nonzero second-partial derivatives of a number of PK parameters, and the total number of such derivatives is large. ROCM12 consists of an integer MSEC variable which takes the value 1 or 0, according as the second-derivatives are needed or not. Consequently, an alternative code to the above might be:
COMMON /ROCM12/ MSEC DIMENSION ETA(6) DOUBLE PRECISION ETA ...
IF (ICALL.EQ.1) THEN
... CALL GETETA (ETA) ... RETURN
ENDIF
...
CALL GETETA (ETA)
...
GG(1,1,1) = TVCLMT*EXP(ETA(4))+TVCLRN*EXP(ETA(5)) GG(1,5,1) = TVCLMT*EXP(ETA(4)) GG(1,6,1) = TVCLRN*EXP(ETA(5))
...
IF (MSEC.EQ.1) THEN
GG(1,5,5) = GG(1,5,1) GG(1,6,6) = GG(1,6,1) ...
ENDIF
where all second-partials are computed and stored only when MSEC equals 1.
By storing a 1 in GG(M,1,1) at ICALL=1, the user
specifies that when ICALL=2 or 4, the subject-specific value
of the logarithm of the Mth PK parameter will be placed in
GG(M,1,1) (see section C). This signal also means that the
subject-specific first derivative of the logarithm of the
Mth PK parameter with respect to
 will be placed in
GG(M,1+K,1) and that the subject-specific second-partial
derivative of the logarithm of the Mth PK parameter with
respect to
will be placed in
GG(M,1+K,1) and that the subject-specific second-partial
derivative of the logarithm of the Mth PK parameter with
respect to 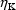 and
and
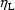 will be placed in
GG(M,1+K,1+L).
will be placed in
GG(M,1+K,1+L).
As mentioned in section C., with every translator
routine, TRANS, there is associated a different list of PK
parameters. These parameters are called the basic PK
parameters. They form a "minimal set" of PK
parameters whose typical/subject-specific values and
 -derivatives must be set in
PK (see sections C and E). There are additional PK
parameters whose use in a given problem are somewhat
optional. In this section we describe them and give some
examples for modeling them. As with the basic parameters,
their typical/subject-specific values and
-derivatives must be set in
PK (see sections C and E). There are additional PK
parameters whose use in a given problem are somewhat
optional. In this section we describe them and give some
examples for modeling them. As with the basic parameters,
their typical/subject-specific values and
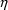 -derivatives are
communicated to PREDPP in PK. The way to do this is
described in section G.
-derivatives are
communicated to PREDPP in PK. The way to do this is
described in section G.
Associated with each observation is an observation compartment
This compartment is specified either explicitly in the event record containing the observation (section V.H), or by a default designation (see sections VI.B and VII.C). For each observation, NONMEM computes a prediction. The amount A in the observation compartment at the time of observation, divided by the value of a parameter S, is used as the prediction. The parameter S is called a scaling parameter
There is one such parameter associated with every compartment of the structural model (including the output compartment).
Suppose the observation is a plasma
concentration. Then the observation compartment should be
taken to be the plasma compartment, and the S of that
compartment should be taken to be the volume of distribution
of that compartment. (Volume of distribution may or may not
also be a basic PK parameter.) Suppose the observation is a
urine concentration. Then the observation compartment should
be taken to be the urine compartment, which in turn might be
identified with the output compartment, and the S of that
compartment should be taken to be the measured volume of
urine. Whereas, as in earlier sections, volume of
distribution is usually modeled in terms of
 ’s,
’s,
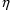 ’s and x, urine
volume is usually a measured quantity and therefore simply
some element of x. However, in principle each scaling
parameter (or any of the PK parameters being described in
section F) can be modeled in terms of
’s and x, urine
volume is usually a measured quantity and therefore simply
some element of x. However, in principle each scaling
parameter (or any of the PK parameters being described in
section F) can be modeled in terms of
 ’s,
’s,
 ’s, and
x.
’s, and
x.
Scaling parameters are optional in the sense that scaling parameters associated with compartments never observed may be ignored. The values of scaling parameters that are not computed in PK are always understood to be 1 (see section G). Therefore, if, an amount, rather than a concentration, is measured, the computation of the scaling parameter may be ignored in this case also. If a scaling parameter is not ignored and is computed in PK to be nonpositive, PREDPP exits with a nonzero PRED error return code (see section K).
The scaling parameter for a given compartment acts discretely at times for which predictions of the scaled amount in this compartment are computed (see section B.2). If volume of distribution is a basic PK parameter, it acts continuously in that capacity. However, when, for example, the scaling parameter for the plasma compartment is set equal to the volume of distribution, the volume parameter acts discretely as it acts through the scaling parameter.
Every dose is associated with a dose compartment
as specified either explicitly in the dose event
record (see section V.H), or by a default designation (see
sections VI.B and VII.C). This compartment is usually the
compartment where the dose is physically input, although it
need not be (see section F.3). If the dose is a bolus dose
or a regular infusion, the dose amount must also be
specified on the dose event record. If the amount is A, an
amount  of drug actually
appears in the dose compartment (either instantaneously at
the time the dose enters the compartment - with a bolus
dose, or over a period of time - with an infusion), where F
is the value of the bioavailability
fraction
of drug actually
appears in the dose compartment (either instantaneously at
the time the dose enters the compartment - with a bolus
dose, or over a period of time - with an infusion), where F
is the value of the bioavailability
fraction
There is one bioavailability fraction (parameter) associated with every possible dose compartment of the structural model (the output compartment is not a possible dose compartment). The bioavailability fraction for a given compartment acts discretely at the times doses enter (or start to enter) the system (see section B.2). For lagged doses, these are lagged times; see section F.6. Bioavailability fractions are optional in the sense that bioavailability fractions associated with compartments never used as dose compartments may be ignored. The values of bioavailability fractions that are not computed in PK are always understood to be 1 (see section G). Therefore, if, bioavailability cannot be estimated, the computation of the bioavailability fraction can be ignored in this case too, with the consequence that it is assumed that the drug is 100% available. If a bioavailability fraction is not ignored and is computed in PK to be negative, PREDPP exits with a nonzero PRED error return code (see section K).
If two different preparations are given into the same dose compartment, and the concomitant Z assumes the value 1 or 2 according to which preparation is being given with some particular dose, then a model for F might be




With this model the typical value of F is
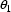 or
or
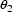 according to the
preparation given. [The variable
according to the
preparation given. [The variable
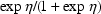 ranges from 0 to 1 and has
typical value
ranges from 0 to 1 and has
typical value  ; so if
; so if
 and
and
 are between 0 and 1, F is
also.] On the other hand, the CV of (random) interindividual
variability in F is approximately the same for both
preparations (viz.
are between 0 and 1, F is
also.] On the other hand, the CV of (random) interindividual
variability in F is approximately the same for both
preparations (viz. 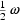 ). Under
this model, if both preparations are given to some
individuals, the bioavailabilities of the two preparations
are perfectly correlated across these individuals (because
with each such individual
). Under
this model, if both preparations are given to some
individuals, the bioavailabilities of the two preparations
are perfectly correlated across these individuals (because
with each such individual 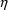 is the same between preparations). With another
model,
is the same between preparations). With another
model,


the correlation depends on the degree to which
 and
and
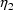 are correlated, which may
be 0. The correlation between
are correlated, which may
be 0. The correlation between
 and
and
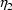 can be estimated (provided
the data allow this); see Guide I. With model (41) the CV of
interindividual variability may differ between preparations
(
can be estimated (provided
the data allow this); see Guide I. With model (41) the CV of
interindividual variability may differ between preparations
( 
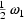 and
and
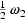 ).
).
There are two types of bolus doses that may be
given. An instantaneous bolus dose of amount A is
such that at the time the dose enters the system, the amount
 of drug appears
instantaneously in the dose compartment, where F is the
value of the bioavailability fraction associated with the
dose compartment. A zero-order bolus dose of amount A
is such that its appearance in the dose compartment is
described by a zero-order process over a finite time
interval, such that the total amount appearing over this
interval of time is
of drug appears
instantaneously in the dose compartment, where F is the
value of the bioavailability fraction associated with the
dose compartment. A zero-order bolus dose of amount A
is such that its appearance in the dose compartment is
described by a zero-order process over a finite time
interval, such that the total amount appearing over this
interval of time is  , where
F is the value of the bioavailability fraction associated
with the dose compartment. The appearance of drug in a depot
compartment, resulting from the dissolution of a preparation
placed therein, is an example of drug appearance that may be
modeled by a zero-order process. The appearance of drug in
the central compartment, resulting from absorption of a
preparation placed in a depot compartment, is another
example of drug appearance that may be modeled by a
zero-order process, although this is often modeled by a
first-order process. In this example, the dose compartment
would need to be the central compartment, even though the
dose was physically input into a depot. A zero-order bolus
dose, just as an instantaneous bolus dose, may have a lag
time, in which case the zero-order process starts at the
lagged time; see section F.6.
, where
F is the value of the bioavailability fraction associated
with the dose compartment. The appearance of drug in a depot
compartment, resulting from the dissolution of a preparation
placed therein, is an example of drug appearance that may be
modeled by a zero-order process. The appearance of drug in
the central compartment, resulting from absorption of a
preparation placed in a depot compartment, is another
example of drug appearance that may be modeled by a
zero-order process, although this is often modeled by a
first-order process. In this example, the dose compartment
would need to be the central compartment, even though the
dose was physically input into a depot. A zero-order bolus
dose, just as an instantaneous bolus dose, may have a lag
time, in which case the zero-order process starts at the
lagged time; see section F.6.
The difference between a regular infusion and a zero-order bolus dose is that the duration of a regular infusion is specified by information in the dose event record and computed by PREDPP itself, whereas the duration of a zero-order bolus dose is regarded as a parameter which may be modeled and computed by the PK routine. Of course, a model for the duration can be as simple as setting this parameter to some data item in the dose record that gives the duration of a regular infusion. Information in the dose record indicates that a dose is a zero-order bolus dose, rather than a regular bolus dose or an infusion; see sections V.E.
There is one duration parameter associated with every possible dose compartment of the structural model. The duration parameter associated with a given compartment acts discretely at the times zero-order bolus doses start to enter the compartment (see section B.2). A zero-order bolus dose whose duration is modeled is called a duration- modeled zero-order bolus dose
Duration parameters are optional in the sense that duration parameters associated with compartments never receiving duration-modeled zero-order bolus doses may be ignored. The values of duration parameters that are not computed in PK are always understood to be 0 (see section G). If a duration parameter is not ignored and is computed in PK to be nonpositive, PREDPP exits with a nonzero PRED error return code (see section K).
Alternatively, the rate of a zero-order bolus dose may be modeled and computed by the PK routine; see next section. Some zero-order bolus doses may be duration-modeled, and others may be rate-modeled.
The zero-order rate of a zero-order bolus dose (see section F.3) may be modeled, instead of its duration. Information in the dose record indicates which is modeled, the duration or the rate; see section V.E. A zero-order bolus dose whose rate is modeled is called a rate-modeled zero-order bolus dose
There is one rate parameter associated with every possible dose compartment of the structural model. These rate parameters are optional in the sense that rate parameters associated with compartments never receiving rate-modeled zero-order bolus doses (or rate-modeled steady-state infusions; see next section) may be ignored. The values of rate parameters that are not computed in PK are always understood to be 1 (see section G). If a rate parameter is not ignored and is computed in PK to be nonpositive, PREDPP exits with a nonzero PRED error return code (see section K).
Rate parameters act continuously. Therefore,
PREDPP obtains the value of a rate parameter, holding over
the state-interval 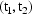 , from a
call to PK with the argument record associated with
, from a
call to PK with the argument record associated with
 , even if the dose event
time occurs before
, even if the dose event
time occurs before 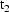 .
Therefore, if there are state times (e.g.
.
Therefore, if there are state times (e.g.
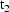 ) falling within the time
interval over which a zero-order bolus dose appears in the
system, there exists the possibility that the rate of drug
input can change during the interval. For this to occur, the
rate parameter would need to be modeled in terms of time
varying concomitant values. As a result, a better
description of the zero-order process where the rate is
modeled might be a piecewise zero-order process. The release
of drug from a sustained release capsule, designed to occur
at different rates at different stages of release, might be
modeled using a rate parameter. This model could be very
simple, depending only on the manufacturer’s design
parameters and not necessarily on parameters whose values
must be estimated.
) falling within the time
interval over which a zero-order bolus dose appears in the
system, there exists the possibility that the rate of drug
input can change during the interval. For this to occur, the
rate parameter would need to be modeled in terms of time
varying concomitant values. As a result, a better
description of the zero-order process where the rate is
modeled might be a piecewise zero-order process. The release
of drug from a sustained release capsule, designed to occur
at different rates at different stages of release, might be
modeled using a rate parameter. This model could be very
simple, depending only on the manufacturer’s design
parameters and not necessarily on parameters whose values
must be estimated.
The duration of a rate-modeled zero-order bolus
dose entering a compartment may be regarded as a derived
parameter, i.e. as a parameter computed by PREDPP from the
primary additional parameters, in this case from the
bioavailability fraction and rate parameter for the given
compartment. This parameter, H, acts discretely at all state
times 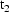 such that there is an
amount
such that there is an
amount 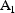 of drug remaining to
be input into the compartment at the state time
of drug remaining to
be input into the compartment at the state time
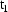 preceding
preceding
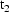 . At
. At
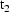 its value is
its value is
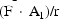 , where F is the
bioavailability fraction applied to the dose at the time it
started to enter the system, and r is the value of the rate
parameter at time
, where F is the
bioavailability fraction applied to the dose at the time it
started to enter the system, and r is the value of the rate
parameter at time  . If one
wants H to be independent of F, r can be set to
. If one
wants H to be independent of F, r can be set to
 , where
, where
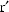 is a nominal rate. For
example, if one wants H to be a given value d (e.g. a
regular infusion is given of known duration d), then one
should set
is a nominal rate. For
example, if one wants H to be a given value d (e.g. a
regular infusion is given of known duration d), then one
should set  . If in fact the
dose is a regular infusion, then A is the amount
. If in fact the
dose is a regular infusion, then A is the amount
 on the dose record, and PK
can obtain this data item. In this case, though, it is
simpler to implement a model for the duration parameter (of
section F.3) than to implement the model for the rate
parameter. If A cannot be obtained as a data item, then in
general the value of H cannot be controlled. One exception
occurs when H is constant all the while the dose enters the
compartment. Then set
on the dose record, and PK
can obtain this data item. In this case, though, it is
simpler to implement a model for the duration parameter (of
section F.3) than to implement the model for the rate
parameter. If A cannot be obtained as a data item, then in
general the value of H cannot be controlled. One exception
occurs when H is constant all the while the dose enters the
compartment. Then set 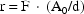 ,
where d is the constant value (so
,
where d is the constant value (so
 ).
).
Since two rate-modeled zero-order bolus doses into the same compartment share the same rate parameter, care should be taken that the intervals over which they appear in the system not overlap, or that if these do overlap, that the two possible values of the rate parameter be the same.
The rate of a (constant rate) steady-state infusion (see section V.F) may be modeled. Such an infusion is called a rate-modeled steady-state infusion
Information in the dose indicates that the infusion is rate-modeled; see section V.E. There is one rate parameter associated with every possible dose compartment of the structural model. The rate parameter that one uses for a given compartment is the same one used to determine the rate of zero-order bolus doses into the compartment. That is, rate-modeled steady-state infusions and zero-order bolus doses into the compartment share the same rate parameter. Rate parameters are optional in the sense that rate parameters associated with compartments never receiving rate-modeled steady-state infusions or rate-modeled zero-order bolus doses may be ignored. The values of rate parameters that are not computed in PK are always understood to be 1 (see section G). If a rate parameter is not ignored and is computed in PK to be nonpositive, PREDPP exits with a nonzero PRED error return code (see section K).
Steady-state infusions are imagined as infusions
which started long before time 0 and terminate at the event
time on the dose event record. Rate parameters act
continuously. In the case of a rate-modeled steady-state
infusion terminating at time t, it should be imagined that
the infusion rate is constant over the infinite interval
from  to t and is obtained
from a call to PK with the argument record associated with
t. Since a rate-modeled zero-order bolus dose and a
rate-modeled steady-state infusion into the same compartment
share the same rate parameter, care should be taken when two
such doses occur, that the infusion does not terminate
during the interval over which the bolus dose appears in the
system, or that if it does, that the two values of the rate
parameter are the same, or that some appropriate strategy is
used.
to t and is obtained
from a call to PK with the argument record associated with
t. Since a rate-modeled zero-order bolus dose and a
rate-modeled steady-state infusion into the same compartment
share the same rate parameter, care should be taken when two
such doses occur, that the infusion does not terminate
during the interval over which the bolus dose appears in the
system, or that if it does, that the two values of the rate
parameter are the same, or that some appropriate strategy is
used.
One possible use of a rate-controlled
steady-state infusion occurs when a patient has been on
chronic drug therapy before entering a study, but one is
uncertain about the dosing history. By modeling this history
with a rate-controlled steady-state infusion (terminating at
time 0) whose typical rate is, say,
 (but which depends also on
an individual random effect), then all compartments are
initialized at the outset with amounts commensurate with the
assumed kinetics, but which will depend on a simple (and
presumably) estimable parameter. For this model to make
sense, one should be able to regard the differences in the
pre-study drug histories between those patients whose
histories are uncertain as being random.
(but which depends also on
an individual random effect), then all compartments are
initialized at the outset with amounts commensurate with the
assumed kinetics, but which will depend on a simple (and
presumably) estimable parameter. For this model to make
sense, one should be able to regard the differences in the
pre-study drug histories between those patients whose
histories are uncertain as being random.
Another possible use is to model the kinetics of a drug which is also present endogenously. As above, a rate-modeled steady-state infusion can be used to initialize the compartments to endongenous amounts. A very large amount of the compound administered thereafter (but with time data item also equal to 0), as a rate-modeled zero-order bolus dose (see section F.4), can maintain the "endogenous steady-state".
The time t on a dose record refers to the recorded time the dose was administered. In the case of a regular infusion, t is the time the infusion was initiated. (In the case of a steady-state infusion, t is the time the infusion terminates, but absorption lag times do not apply to steady-state infusions.) An absorption lag time is an increment of time L such that the time that the dose is regarded (by PREDPP) as entering (or starting to enter) the system is t+L. An absorption lag time is sometimes simply called the lag time
The time t+L is called the lagged time
and a dose with a positive lag time is called a lagged dose
Absorption lag times act discretely at recorded dose times. That is, at such an event time t an absorption lag time L for the dose is computed by the PK routine. The lagged time t+L is not an event time; it is a nonevent dose time. If there actually is an event time coinciding with the lagged time, this is only coincidental. The bioavailability fraction and duration parameter act at the time t+L, when the dose actually enters (or starts to enter) the system. Normally, PK is called to compute these parameters with only the argument record associated with t+L. This record generally does not contain information that might be used in the computation. If PK requests calls at nonevent dose times (see section III.H), PK can compute these parameters using both the argument record associated with t+L and the the dose record describing the initiating dose.
When additional doses are specified on a dose event record (see section V.K), the absorption lag time acting at the time on the dose record applies to the dose and to all the additional doses. In this case the lag time should not exceed the (length of the) interdose interval. With a steady-state multiple dose (see section V.F) the absorption lag time applies not only to this dose, but also to all the preceding implied doses. With such a dose, the lag time should not exceed the interdose interval.
There is one absorption lag time (parameter) associated with every possible dose compartment of the structural model (the output compartment is not a possible dose compartment). Absorption lag times are optional in the sense that absorption lag times associated with compartments never used as dose compartments may be ignored. The values of absorption lag times that are not computed in PK are always understood to be 0 (see section G). If an absorption lag time parameter is not ignored and is computed in PK to be negative, PREDPP exits with a nonzero PRED error return code (see section K).
As with any PK parameter, a lag time may be
modeled in as complicated a way as is desired; the model may
include  ’s. However,
data can often be insufficient to allow a lag time to be
well-estimated, and even when a typical lag time can be
estimated well enough, one may not be able to estimate the
interindividual variance of the lag time. In this case
either set the variance set to zero, or do not use an
’s. However,
data can often be insufficient to allow a lag time to be
well-estimated, and even when a typical lag time can be
estimated well enough, one may not be able to estimate the
interindividual variance of the lag time. In this case
either set the variance set to zero, or do not use an
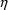 .
.
With any of the kinetic models a (peripheral) output compartment is always present. Associated with this compartment is a PK parameter, the output fraction
denoted here by  . Of the entire amount,
. Of the entire amount, 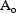 ,
of drug introduced into the system by various dosage
patterns and then eliminated from the system during a
state-interval, a fraction of this amount,
,
of drug introduced into the system by various dosage
patterns and then eliminated from the system during a
state-interval, a fraction of this amount,
 , goes into this output
compartment. The output compartment may be turned on and
off. While on, drug accumulates therein, and when turned
off, the amount therein is reset to zero. So, for example,
if the output compartment is regarded as a urine
compartment, and
, goes into this output
compartment. The output compartment may be turned on and
off. While on, drug accumulates therein, and when turned
off, the amount therein is reset to zero. So, for example,
if the output compartment is regarded as a urine
compartment, and  is the
ratio of renal to total clearance, the initiation and
termination of a urine collection can be
simulated.
is the
ratio of renal to total clearance, the initiation and
termination of a urine collection can be
simulated.
If the output compartment is never turned on, the output fraction can be ignored. If the value of the output fraction is not computed in PK, it is always understood to be 1 (see section G). Consequently, if the output fraction is ignored, then the amount in the output compartment would eventually equal 100% of all drug input into the system, provided the system does not retain any drug indefinitely, drug administration finally ceases, and the output compartment is always on. If the output fraction is not ignored and is computed in PK to be less than 0 or greater than 1, PREDPP exits with a nonzero PRED error return code (see section K). The output fraction acts continuously.
The example mentioned above might, more specifically, be

where 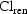 and Cl are
given as in (17) and (18). Under this model, the typical
value of
and Cl are
given as in (17) and (18). Under this model, the typical
value of  is
is

and the subject-specific first-partial derivatives are


The use of  depends on the assumption that the rate of change of drug
amount in the output compartment is linear in the other
compartment amounts. Other than this linearity restriction,
the system can be nonlinear.
depends on the assumption that the rate of change of drug
amount in the output compartment is linear in the other
compartment amounts. Other than this linearity restriction,
the system can be nonlinear.
In earlier sections it has been suggested that unexplained interindividual variablity in kinetic responses might be modeled in terms of random interindividual effects on familiar kinetic parameters. Alternatively, a population kinetic model can be entertained wherein at least some of the unexplained interindividual variability is attributable to what appears to be random differences between individuals’ biological clocks. A simple low-dimensional description of unexplained interindividual variability, albeit somewhat empirical, results when all such variability is attributed to this source and to random interindividual differences in scaling parameters.
According to this idea, time itself is scaled differently between individuals. However, since some time intervals, such as an infusion time, are always measured on an external clock (e.g. the nurse’s wrist-watch), time is scaled only where it multiplies a rate constant (of a linear model). The scaling parameter is an additional PK parameter X which is modeled in PK. This parameter is called the time scale parameter (or sometimes, the X parameter ). There is a single time scale parameter that applies to all rate constants. The parameter acts continuously (and could therefore theoretically itself vary with time measured on an external clock). It can only be used with linear kinetic models. If it is not used, it can be ignored. If the value of the time scale parameter is not computed in PK, it is always understood to be 1 (see section G). If it is not ignored and is computed in PK to be nonpositive, PREDPP exits with a nonzero PRED error return code (see section K).
Random interindividual effects can be assumed to affect the time scale parameter and the scaling parameters (see section F.1). If x denotes time, and S is a scaling parameter, then (ignoring random intraindividual variability) an observation y can be written schematically as
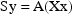
where A is drug amount as a function of time, and where, say,
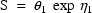
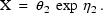
Time x may be regarded as the abscissa value, the observation y may be regarded as the ordinate value, and then one sees that X scales the abscissa and S scales the ordinate. Random interindividual kinetic differences are being attributed at least in part to random interindividual differences in the abscissa and ordinate scales.
The X parameter does not scale the duration
parameter D of a duration-modeled zero-order bolus dose. If
this is desired, this must be done by setting
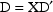 , where
, where
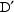 is an unscaled duration
parameter.
is an unscaled duration
parameter.
The argument ICALL of PK was described in section
III.C. It functions similarly to the ICALL argument
described in Guide I, section C.4.2. It has 3 possible
values when PK is called. The value 1 signals to PK that the
routine is being called for the first time in the NONMEM
problem. At such a time PK must store certain values in
array IDEF, telling PREDPP what, if any, additional PK
parameters the user has chosen to model, and where their
typical/subject-specific values and
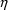 -derivatives will be stored
in the GG array. Usually, a model for at least one
additional parameter, e.g. a scaling parameter, is given in
PK. IDEF is either a one- or two-dimensional array. The
two-dimensional format is the most convenient one to use,
and it is described in this section. To see how the
two-dimensional formatted IDEF is declared in PK, see
section C. With PREDPP versions I and II only the
one-dimensional format is allowed. This format is retained
for the convenience of previous users, and it is described
in Appendix III. However, if IDEF is to convey
information not applicable in PREDPP versions I and II, the
two-dimensional format must be used. For example, if an
absorption lag time is being modeled, this information must
be conveyed by the two-dimensional formatted IDEF. To use
the two-dimensional format, set IDEF(1,1) to -9 at ICALL=1.
Otherwise, PREDPP assumes that the one-dimensional format is
being used (even when IDEF is declared two-dimensional in
the DIMENSION statement).
-derivatives will be stored
in the GG array. Usually, a model for at least one
additional parameter, e.g. a scaling parameter, is given in
PK. IDEF is either a one- or two-dimensional array. The
two-dimensional format is the most convenient one to use,
and it is described in this section. To see how the
two-dimensional formatted IDEF is declared in PK, see
section C. With PREDPP versions I and II only the
one-dimensional format is allowed. This format is retained
for the convenience of previous users, and it is described
in Appendix III. However, if IDEF is to convey
information not applicable in PREDPP versions I and II, the
two-dimensional format must be used. For example, if an
absorption lag time is being modeled, this information must
be conveyed by the two-dimensional formatted IDEF. To use
the two-dimensional format, set IDEF(1,1) to -9 at ICALL=1.
Otherwise, PREDPP assumes that the one-dimensional format is
being used (even when IDEF is declared two-dimensional in
the DIMENSION statement).
Just as typical/subject-specific values and
 -derivatives for each of
the basic PK parameters are stored in some row of the GG
array, so are typical/subject-specific values and
-derivatives for each of
the basic PK parameters are stored in some row of the GG
array, so are typical/subject-specific values and
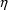 -derivatives for each of
the additional PK parameters. The rows can be assigned
somewhat arbitrarily. If the output fraction is modeled, set
IDEF(2,1) to the number of the row, called the row
index
-derivatives for each of
the additional PK parameters. The rows can be assigned
somewhat arbitrarily. If the output fraction is modeled, set
IDEF(2,1) to the number of the row, called the row
index
chosen for this fraction. If the time scale parameter is modeled, set IDEF(2,2) to the row index chosen for this parameter. If the scaling parameter, bioavailability fraction, rate parameter, duration parameter, or absorption lag for the Ith compartment is modeled, set IDEF(3,I), IDEF(4,I), IDEF(5,I), IDEF(6,I), or IDEF(7,I), respectively, to the row index chosen for this parameter.
There is a number,
 , that is the largest
number of basic parameters permitted with the selected
kinetic model. This number is either set in the selected
ADVAN subroutine (see section VII.C) or set by the user via
the MODEL subroutine (see section VI.B). A row index M
assigned to an additional PK parameter must be a number
greater than
, that is the largest
number of basic parameters permitted with the selected
kinetic model. This number is either set in the selected
ADVAN subroutine (see section VII.C) or set by the user via
the MODEL subroutine (see section VI.B). A row index M
assigned to an additional PK parameter must be a number
greater than  , but no
greater than 30. Consider, for example, the one compartment
linear model, with one basic PK parameter: rate constant of
elimination. (This parameterization is implemented via
TRANS1.) From section VII.C.1 it may be seen that
, but no
greater than 30. Consider, for example, the one compartment
linear model, with one basic PK parameter: rate constant of
elimination. (This parameterization is implemented via
TRANS1.) From section VII.C.1 it may be seen that
 . If the scaling parameter
for compartment 1 is to be modeled, then one can set
IDEF(3,1)=3. If the scaling parameter for compartment 2 is
also to be modeled, then one can set IDEF(3,2)=4. Lastly, if
the bioavailability fraction for compartment 2 is to be
modeled, one can set IDEF(4,2)=5
. If the scaling parameter
for compartment 1 is to be modeled, then one can set
IDEF(3,1)=3. If the scaling parameter for compartment 2 is
also to be modeled, then one can set IDEF(3,2)=4. Lastly, if
the bioavailability fraction for compartment 2 is to be
modeled, one can set IDEF(4,2)=5
The row indices of the additional PK parameters
must be consecutive integers beginning with
 , with no integers
skipped, as in the above example. However, one is not
restricted to preserving an increasing monotonic
relationship between the numbers of the compartments and
their row indices, or between the numbers of the rows of
IDEF itself and the row indices. So, in the above example
one can just as well set IDEF(3,1)=4 and IDEF(3,2)=3, or set
IDEF(3,1)=4, IDEF(3,2)=5, and IDEF(4,2)=3. Nor is one
restricted from using a row index more than once. So, one
can set IDEF(3,1)=IDEF(3,2)=3 (which specifies that the
scaling parameters for compartments 1 and 2 are modeled and
that their values are to be equal and stored in row 3 of
GG), though usually there is no need to do this.
, with no integers
skipped, as in the above example. However, one is not
restricted to preserving an increasing monotonic
relationship between the numbers of the compartments and
their row indices, or between the numbers of the rows of
IDEF itself and the row indices. So, in the above example
one can just as well set IDEF(3,1)=4 and IDEF(3,2)=3, or set
IDEF(3,1)=4, IDEF(3,2)=5, and IDEF(4,2)=3. Nor is one
restricted from using a row index more than once. So, one
can set IDEF(3,1)=IDEF(3,2)=3 (which specifies that the
scaling parameters for compartments 1 and 2 are modeled and
that their values are to be equal and stored in row 3 of
GG), though usually there is no need to do this.
For each scaling parameter and bioavailability
fraction, and for the output fraction and time scale
parameter, PREDPP assumes that if its row index is not
explicitly set at ICALL=1, then its typical/subject-specific
value is always 1, and its  -derivatives are always 0. Therefore, for example, the row
index of a bioavailability fraction associated with a plasma
compartment receiving only intravenous bolus doses
need not be explicitly set. (If this compartment were also a
dose compartment for zero-order bolus doses with possibly
less than 100% bioavailability, the row index would need to
be set. In this case one would need to be careful that the
fraction stored is less than 1 only when the fraction for
the zero-order bolus dose is being obtained with the call to
PK.) For each absorption time lag, PREDPP assumes that if
its row index is not explicitly set at ICALL=1, then its
typical/subject-specific value is always 0, and its
-derivatives are always 0. Therefore, for example, the row
index of a bioavailability fraction associated with a plasma
compartment receiving only intravenous bolus doses
need not be explicitly set. (If this compartment were also a
dose compartment for zero-order bolus doses with possibly
less than 100% bioavailability, the row index would need to
be set. In this case one would need to be careful that the
fraction stored is less than 1 only when the fraction for
the zero-order bolus dose is being obtained with the call to
PK.) For each absorption time lag, PREDPP assumes that if
its row index is not explicitly set at ICALL=1, then its
typical/subject-specific value is always 0, and its
 -derivatives are always 0.
PREDPP assumes that if neither the row index of the duration
parameter nor the row index of the rate parameter for a
given compartment is explicitly set at ICALL=1, then the
compartment never receives zero-order bolus
doses.
-derivatives are always 0.
PREDPP assumes that if neither the row index of the duration
parameter nor the row index of the rate parameter for a
given compartment is explicitly set at ICALL=1, then the
compartment never receives zero-order bolus
doses.
The user can specify that the
typical/subject-specific value and the
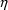 -derivatives of the
logarithm of an additional PK parameter will be placed in
GG, just as with the logarithm of a basic PK parameter (see
sections C and E).
-derivatives of the
logarithm of an additional PK parameter will be placed in
GG, just as with the logarithm of a basic PK parameter (see
sections C and E).
As the pharmacokinetic system is advanced, PK is called one or more times, each time with some argument record. The event records comprise these argument records, and are passed to PK in time order. The simulation and/or data analytic computations will normally be done correctly if routine PK is called with one event record after another (within an individual record), no event records being skipped, and no event record being repeated. This is the default. However, PREDD can implement a few different protocols for calling PK. A protocol is specified by setting IDEF(1,2) to one of various values at ICALL=1 (for more about IDEF, see section G). For example, with Version II of PREDPP the PK routine can be called only with the first event record of the individual record and with every event record thereafter where the time data item differs from the time data item of the previous event record (this is the default with Version II). If this more limited sequence of calls is desired (perhaps because existing PK code takes advantage of this older protocol), this can be accomplished by setting IDEF(1,2)=0. Note, though, that in this case, IDEF(1,2) must be explicitly set to 0.
Often, none of the basic or additional PK parameters depend on concomitant variables whose values vary within an individual record, i.e. vary over time. In this situation the information output by PK, i.e. the GG array, is the same for each event record of an individual record (for fixed THETA and ETA). Considerable computation time can be saved; PREDPP need call PK only once per individual record, with the first event record only (for any given values of the THETA and ETA arrays). The values of continuously acting PK parameters computed with this call can be assumed to hold over all state-time intervals for the individual record, and the values of discretely acting PK parameters can be assumed to hold at each state time for the record. The user can request this calling-protocol by setting IDEF(1,2)=1. This is illustrated in examples below; see sections L.1 and L.2.
When the data are from a single subject, PREDPP treats all event records in the entire data set as though they are associated with the same subject. (This is a consequence of the single-subject assumption; see section IV.A.) In particular, suppose that every call to PK with a different event record results in the same output from PK (for fixed THETA). Then only one call is necessary, a call with the first event record in the entire data set. The values of continuously acting PK parameters computed at this call can be assumed to hold over all state-time intervals for the entire data set, and the values of discretely acting PK parameters can be assumed to hold at all state times for the entire data set. Setting IDEF(1,2) to 1 has this effect. This is illustrated in examples below; see sections L.3 and L.4.
Even when IDEF(1,2)=0 or 1, a call to PK with any given event record can be forced with the use of the CALL data item (see section V.J).
The protocol where PK is called once with every event record (see above) can be specified by setting IDEF(1,2) to -1, or by not setting IDEF(1,2) at all, i.e. this protocol is the default. If it is desired that, in addition, the values of PK parameters at any nonevent dose time t be computed with access to both the argument record associated with t and the event record describing the dose (see section B.2), set IDEF(1,2)=-2. This has the effect that PK may be called repeatedly with the same event record (for if t is a nonevent dose time, and s is the subsequent event time, PK is called with the event record for s at both times t and s). The primary use of this protocol is so that the values of certain discretely acting PK parameters, the bioavailability fractions and duration parameters, can always be computed with access to useful dose-related concomitant information contained in the dose record, such as the type of preparation. In the next section the way PK has access to the record describing the dose is explained.
PK can access information other than though its argument list. There are a number of read-only commons to which it has access. Firstly, there are the NONMEM read-only commons to which any PRED has access: ROCM11, ROCM12, ROCM13, ROCM14, and ROCM15. These are FORTRAN named commons. Descriptions of ROCM11 and ROCM12 are given in sections L.2 and E.4, respectively. Information about ROCM13-ROCM15 may be obtained by consultation with the NONMEM Project Group. Secondly, there are PREDPP read-only commons. These are FORTRAN named commons whose names are of the form PROCMx, where x is an integer.
COMMON /PROCM1/ NEWIND
NEWIND is an integer variable acting like the NEWIND variable described in Guide I. It assumes one of 3 values: 0 if the event record is the first of the entire data set, 1 if the event record is the first event record of an individual record (other than the first individual record), and 2 if the event record is other than the first event record of an individual record. When the data are single-subject data, individual records are as described in chapter II.
COMMON /PROCM2/ DOST,DDOST(10),D2DOST(10,10)
When IDEF(1,2)=-2, the values of PK parameters at any nonevent dose time t are obtained with access to both the argument record associated with t and the event record describing the dose (see sections B.2 and H). At the call to PK, when the values of the PK parameters are obtained, the value of t itself can be found in DOST. The event time when the dose is given is found in another read-only common (PROCM3; see below).
The time t may depend on
 ’s. The first-partial
derivatives and the second-partial derivatives of t with
respect to the
’s. The first-partial
derivatives and the second-partial derivatives of t with
respect to the 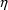 ’s are
given in DDOST and D2DOST, respectively. DDOST(K) =
’s are
given in DDOST and D2DOST, respectively. DDOST(K) =
 , and DDOST(L,K) =
, and DDOST(L,K) =
 for
for
 . When using double
precision, DOST and the arrays DDOST and D2DOST must be
declared DOUBLE PRECISION. When PK is called at an event
time, DOST, DDOST and D2DOST contains
0’s.
. When using double
precision, DOST and the arrays DDOST and D2DOST must be
declared DOUBLE PRECISION. When PK is called at an event
time, DOST, DDOST and D2DOST contains
0’s.
COMMON /PROCM3/ DOSREC(20)
When IDEF(1,2)=-2, the values of discretely acting PK parameters at any nonevent dose time t are obtained with access to both the argument record associated with t and the event record describing the dose (see sections B.2 and H). At the call to PK, when the values of the PK parameters are obtained, the (last data record of the) event record describing the dose can be found in DOSREC. (The event record can span several data records; see chapter II.) This record differs from the argument record (the event record found in the argument EVTREC), which is the event record at the next event time following t. The argument record may not even be a dose record, but if it is, it may describe a dose unlike the one entering at time t.
DOSREC is always a single precision array. When PK is called at an event time, DOSREC contains 0’s.
A value stored in a variable (or array element) V in PK may be displayed in a table or scatterplot. To accomplish this, common NMPRD4 must be included in PK, and V must be listed in NMPRD4. (When there is more than one data record within an event record R2, the value of V computed when PK is called with the preceding event record R1 is displayed as part of the last data record of R1, and as part of every data record but the last in R2.) See the example in section L.2. More information about the display of PK-defined items may be obtained by consultation with the NONMEM Project Group. Common NMPRD4 also provides a convenient place to store values of variables to be shared between PK and other user routines, and it is used thusly when these routines are generated from NM-TRAN abbreviated code (see Guide IV).
The declarations for NMPRD4 should look like:
COMMON /NMPRD4/ V1, V2, ..., VN DIMENSION COM(1000) EQUIVALENCE (COM(1),V1) and if double precision NONMEM is used: DOUBLE PRECISION COM,V1,V2, ..., VN
where the names of the variables listed in the common should be similar to those shown, but could, of course, differ. It is necessary to introduce the array COM, and to include the DIMENSION and EQUIVALENCE statements, only to guarantee that the length of NMPRD4 is the same in PK as it is in other NONMEM/PREDPP routines where its length is 1000. The length 1000 is a default value; if it is changed (see Guide III, section III.2.7), then the number 1000 is changed accordingly in the above DIMENSION statement.
Common NMPRD3 may also be included in PK. COMACT may be tested, and COMSAV may be set. The declarations for NMPRD3 should look like:
COMMON /NMPRD3/ COMACT,COMSAV INTEGER COMACT,COMSAV
where the names of the variables listed in the common should be similar to those shown, but could, of course, differ.
PREDPP may exit with a nonzero PRED error return code. Then either the NONMEM run is immediately aborted or an error-recovery procedure is implemented. An error-recovery procedure entails continued calls to PRED, but with values of THETA or ETA different from those with previous calls which resulted in nonzero return codes. There are two error-recovery procedures: one with which different ETA values are tried, the ETA-recovery a second with which different THETA (and possibly ETA) values are tried, the THETA-recovery
Whenever it is possible to implement the ETA-recovery, this is done. If this procedure fails, or if it is not possible to implement the ETA-recovery, and the error return code is obtained during either the search in the Estimation Step or the search in the Initial Estimation Step, then a choice exists between an abort and implementation of the THETA-recovery. If the THETA-recovery fails, or if it is not actually possible to implement the THETA-recovery, the NONMEM run is aborted.
A PRED error return code can have values 0, 1, or 2. The value 0 means that the return is a normal return. The value 1 means that if the choice exists between an abort or implementation of the THETA-recovery, then this choice is to be made using control stream information. The value 2 means that if the choice exists between an abort or implementation of the THETA-recovery, then the abort should be chosen.
When an abort occurs, an error message will appear in the NONMEM output, in the intermediate output file (if such a file exists), and in the PRED Error file. When the THETA-recovery is implemented, an error message appears in the intermediate output file (if such a file exists), in the PRED Error file, and if recovery is not possible, in the NONMEM output. The error message is called a PRED error message
When the PRED error return code is 1, and a choice exists between implementation of the THETA-recovery and an abort, the THETA-recovery is implemented if the value in field 1 (field 3) of the ESTIMATION (THETA CONSTRAINT) record is 1 (or with NM-TRAN, if the NOABORT option is used in the $ESTIMATION ($THETA) record). If the value is 0 (or if the NOABORT option is not used), then the run is aborted. Often, the most appropriate response to an abort occuring during the Initial Estimate Step, or during the Estimation Step after the 0th iteration summary has been output, is to rerun the problem requesting that the THETA-recovery be implemented. Warning: If the implementation of the THETA-recovery is requested before an actual abort has occured, be sure to check the PRED Error file for possibly useful diagnostic information that is otherwise available in NONMEM output when an abort occurs.
More information about PRED error-recovery may be obtained by consultation with the NONMEM Project Group.
PREDPP may exit with a nonzero PRED error return code as a result of some computation undertaken in a PREDPP kernal or Library routine, or when PK returns an invalid value of a PK parameter. The nature of the problem will be described in the PRED error message if this message appears.
PK can force an immediate return to NONMEM from PREDPP with a nonzero PRED error return code and accompanying user message. The contents of GG are ignored. If a user message is returned, it will appear as part of the PRED error message. To accomplish this, commons NMPRD1 and NMPRD2 must be included in PK. The return code is stored in an integer variable listed as the first element of NMPRD1. The user message can be comprised of up to three character strings, each of length 132. The message is stored in a character string array of length 3 listed in common NMPRD2.
The declarations for NMPRD1 and NMPRD2 should look like:
COMMON /NMPRD1/ IERPRD,NETEXT COMMON /NMPRD2/ ETEXT(3) INTEGER IERPRD,NETEXT CHARACTER*132 ETEXT
where the names of the variables listed in the common should be similar to those shown, but could, of course, differ. It is necessary to include the variable NETEXT only to guarantee that the length of NMPRD2 is the same in PK as it is in other NONMEM/PREDPP routines. PREDPP sets its value appropriately.
One example of code for a PK routine involves the simple one compartment linear model. It is based on an analysis of phenobarbitol data (which may be found on a file of the NONMEM distribution medium; see Guide III). More detailed discussion of the data set is to be found in section V.L.1. Essentially, each of 59 neonates was given some loading dose of the drug, had a plasma drug level measured about 2 hours later, was given maintenance doses about every 12 hours thereafter, had possibly one trough level measured during maintenance dosing, and certainly one level measured some time after the last maintenance dose. Due to the long half-life of the drug, for the purposes of analysis all doses can be regarded as intravenous bolus doses. The weight and APGAR score of each individual are available as concomitant information. The APGAR score (1-10) is a measure of a neonate’s health at birth.
The one compartment linear model is implemented
by choosing subroutine ADVAN1 from the PREDPP Library (see
chapter I). The user chooses to parameterize this model in
Cl and Vd, so the routine TRANS2 is also chosen from the
Library (see section A). Cl is modeled as in (14), with
 taken to be proportional to
weight as in (2) (see section D). Vd is also modeled as in
(14), with
taken to be proportional to
weight as in (2) (see section D). Vd is also modeled as in
(14), with  taken to be
proportional to weight as in (2); however the
proportionality constant is one of two possibly different
values depending on the APGAR score. If APGAR is 2 or less,
the proportionality constant is one value, and if APGAR is
greater than 2, the proportionality constant is possibly
another value.
taken to be
proportional to weight as in (2); however the
proportionality constant is one of two possibly different
values depending on the APGAR score. If APGAR is 2 or less,
the proportionality constant is one value, and if APGAR is
greater than 2, the proportionality constant is possibly
another value.
A code for PK is given in Figure 1. (A
corresponding NM-TRAN abbreviated code is shown in Figure 17
as part of an NM-TRAN control stream.) It returns typical
values and typical first-partial derivatives. It can be used
with the first-Order estimation method, but not with
conditional estimation methods or with posthoc estimation of
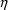 ’s. Note that the row
index of the scaling parameter for the plasma (i.e. central)
compartment is set at ICALL=1 to be 3 and that this
parameter is identified with Vd. Also note that since both
weight and APGAR do not vary within an individual over time,
it is stipulated at ICALL=1 that at ICALL=2, PK be called
only once per individual record.
’s. Note that the row
index of the scaling parameter for the plasma (i.e. central)
compartment is set at ICALL=1 to be 3 and that this
parameter is identified with Vd. Also note that since both
weight and APGAR do not vary within an individual over time,
it is stipulated at ICALL=1 that at ICALL=2, PK be called
only once per individual record.
A second code for PK is given in Figure 2. (The
NM-TRAN abbreviated code shown in Figure 17 would work just
as well for this second code as for the first code.) It is
shown to illustrate the use of PK with the Simulation Step.
Upon inspecting it, one should imagine that drug levels are
being simulated under the same model as decribed above, and
with the same dosing and observation designs and same
subject-specific values for the covariables weight and APGAR
score as pertain to the real drug level data. One should
further imagine that these simulated data are then analyzed
as described above. The code at ICALL=2 is exactly like that
of Figure 1. At ICALL=4 values for the
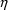 variables are obtained
using the NONMEM utility SIMETA (see Guide IV, section
III.B.13), subject-specific values of the PK parameters are
computed under the given model, but
variables are obtained
using the NONMEM utility SIMETA (see Guide IV, section
III.B.13), subject-specific values of the PK parameters are
computed under the given model, but
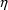 -derivatives are not
computed.
-derivatives are not
computed.
It is, of course, possible to simulate data using one model for the PK parameters and to analyze these data using another by allowing the codes at ICALL=2 and ICALL=4 to implement different models. Structural kinetic differences between simulation and analysis models may be accommodated using an ADVAN implementing one of the general linear or nonlinear models (see chapter VI), or by simulating data in one NONMEM run with one model and analyzing them in another NONMEM run with another model.
One also sees in Figure 2 that the 6th data item of each data record is modified to be 1 or 2 according as the APGAR score is or is not, respectively, greater than 2. This indicator type data item might serve to partition scatterplots. In general, data items (not required by NONMEM or PREDPP) can be modified at ICALL=4 (but not at ICALL=2; see also section VI.A). However when using PREDPP, only data items in the last data record of an event record can be modified; modifications of data items in data records other than the last data record are simply ignored.
A third code is given in Figure 3. It returns
subject-specific values and subject-specific first-partial
derivatives (but is not meant to be used with simulation).
It can be used with conditional estimation methods and with
posthoc estimation of the  ’s, in particular, but also with the first-Order
estimation method. (The NM-TRAN abbreviated code shown in
Figure 17 would work just as well for this third code as for
the first and second codes. However, yet another NM-TRAN
control stream with this same abbreviated code, but
explicitly requesting the computation of posthoc estimates,
is given in Figure 21.)
’s, in particular, but also with the first-Order
estimation method. (The NM-TRAN abbreviated code shown in
Figure 17 would work just as well for this third code as for
the first and second codes. However, yet another NM-TRAN
control stream with this same abbreviated code, but
explicitly requesting the computation of posthoc estimates,
is given in Figure 21.)
With this example, the data set of example I is
again used, and again, the kinetic model is the one
compartment linear model parameterized in Cl and Vd, and Cl
and Vd are modeled as in (14). However, weight is now
ignored, and  and
and
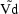 are modeled as in (1), i.e.
taken simply to be elements of
are modeled as in (1), i.e.
taken simply to be elements of
 . With no further changes
to example I, the fit is poor, as seen in the scatterplot of
CP (measured plasma concentration) vs PRED in Figure 4. If
we pretend that weight has not even been recorded, there is
little that can done to substantially improve the fit by
introducing concomitant variables into the model; the APGAR
score is not a very important covariable. We can try to
include a correlation between the two
. With no further changes
to example I, the fit is poor, as seen in the scatterplot of
CP (measured plasma concentration) vs PRED in Figure 4. If
we pretend that weight has not even been recorded, there is
little that can done to substantially improve the fit by
introducing concomitant variables into the model; the APGAR
score is not a very important covariable. We can try to
include a correlation between the two
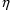 -variables, and this
reduces the minimum value of the objective function about 15
points. (This is partially explained by the fact that weight
has a considerable effect on both CL and Vd.) However, the
scatterplot of CP vs PRED in Figure 4 actually results from
a run with which the correlation is already
included.
-variables, and this
reduces the minimum value of the objective function about 15
points. (This is partially explained by the fact that weight
has a considerable effect on both CL and Vd.) However, the
scatterplot of CP vs PRED in Figure 4 actually results from
a run with which the correlation is already
included.
There is, though, some reason to entertain the idea (see below) that the 59 neonates constitute a random sample from a population comprised of two subpopulations, one with one set of typical values of Cl and Vd, and a second with another set of typical values, even though nothing is recorded about a neonate that would indicate of which subpopulation he is a member. A mixture model, a model that explicitly assumes that some fraction p of the population has one set of typical values of CL and Vd, and that the remaining fraction 1-p has another set of typical values, describes such a population and may be fit to the data. Both sets of typical values and the mixing fraction p may be estimated. This example shows how to implement such a model.
If it were known that CL and Vd were both proportional to weight (and we might justifiably suppose this much is known) and that weight were bimodally distributed in the population, this would clearly justify the mixture model assumption. However, from the recorded weights there is no evidence that weight is bimodally distributed. There is evidence, though, that weight is very right-skewed, and the assumed mixture model can also describe a unimodel right-skewed distribution, bivariate in CL and Vd (although, other types of models can also describe the same kind of distribution). It is for this reason that such a model might be tried.
The fit with the mixture model does indeed result in such a distribution (see section V.L.2). The minimum value of the objective function is reduced by another 15 points. Also, it is interesting to see how retrospectively, weight can be related to a classification of the 59 neonates into two groups as suggested by the fitted mixture model.
The mixture model is given by:
For subpopulation 1:
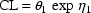
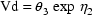
For subpopulation 2:
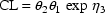
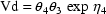
The parameters  and
and  are the fractional
differences in the typical values between the two
subpopulations. With a mixture model, different
are the fractional
differences in the typical values between the two
subpopulations. With a mixture model, different
 variables on the same PK
parameter must be used with different subpopulations.
Certainly, when the magnitude of the dispersion of the
parameter within a subpopulation differs between
subpopulations, it should be clear that different
variables on the same PK
parameter must be used with different subpopulations.
Certainly, when the magnitude of the dispersion of the
parameter within a subpopulation differs between
subpopulations, it should be clear that different
 variables must be used, but
this rule actually applies even when the magnitudes are the
same.
variables must be used, but
this rule actually applies even when the magnitudes are the
same.
A code is given in Figure 5, returning subject-specific values and subject-specific first-partial derivatives. (A corresponding NM-TRAN abbreviated code is shown in Figure 23 as part of an NM-TRAN control stream.) The integer variable MIXNUM, found in read-only common ROCM11, has value 1 or 2 according to whether NONMEM requires PRED to compute outputs for the 1st or 2nd subpopulations, respectively. Accordingly, PK computes different outputs according to the value of MIXNUM. MIXNUM first assumes the value 1, and then PK is called with event records from an individual record. Then MIXNUM assumes the value 2, and PK is called with the event records from the same individual record. This process is carried out for each individual record, and, of course, for each individual record repeatedly as parameter values vary.
For each individual, NONMEM computes an estimate of the number of the subpopulation of which the individual is a member, and it stores this estimate in the integer variable MIXEST, also found in ROCM11. When PK is called with any event record from an individual’s record, the value of MIXEST is the estimate for the individual, although, this value is 1 for all calls to PK preceding the computation of the estimates. By the time the computations for the Table and Scatterplot Steps are performed, these estimates are actually available, and storing them in some variable EST, listed in common NMPRD4, during calls to PK while these steps are being implemented, enables the estimates to be displayed in tables and scatterplots. The control stream requesting the display is described in section V.L.4.
A code for the user-supplied routine MIX is given in Figure 6. This routine is required when a mixture model is used. It is called with one individual record after another. Each time it is called the fractions p and 1-p are computed and stored in the array P. In this example p is simply THETA(5) (and is estimated, but constrained to be between 0 and 1; see section V.L.2). The number of subpopulations is stored in the variable NSPOP (in principle, this number, as well as the fractions associated with each subpopulation, can change from individual to individual). The current value of THETA is found in read-only common ROCM0, and if required, data items from the observation records of the individual record can be found in another read-only common. More information concerning these commons may be obtained by consultation with the NONMEM Project Group.
Another example of code for a PK routine involves the one compartment linear model with first order absorption. It is based on the very same example used in Guide I, section C - the simple nonlinear regression example using theophylline data. Although PREDPP has been designed with population pharmacokinetic data analysis in mind (where there are data from a number of subjects), the user can also take advantage of the ability with PREDPP to facilitate pharmacokinetic computations when the data come from a single subject. The simple nonlinear regression example illustrates how to use PREDPP with such data. In this example a single bolus dose is given to the subject, and then plasma concentrations are observed. Therefore, this example, though typical of single-subject data, does not really illustrate the power of PREDPP. It is simple enough that a user-supplied PRED, such as the one given in Guide I, can be developed rather quickly by most users. Were multiple dosing involved, or a more complicated kinetic model used, the advantage in using PREDPP would be clearer.
The code for PK is given in Figure 7. (A
corresponding NM-TRAN abbreviated code is shown in Figure 26
as part of an NM-TRAN control stream.) The user-chosen
parameters are the rate constants of elimination and
absorption. Since all the data are from a single subject,
random effects describing subject-to-subject variability are
unnecessary. So,  type
random variables do not appear in the model for the PK
parameters, and neither ETA variables nor
type
random variables do not appear in the model for the PK
parameters, and neither ETA variables nor
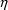 -derivatives are computed
in the PK routine. The typical values of the PK parameters
are just the subject’s values of these parameters. In
principle these could be modeled in terms of concomitant
variables, e.g. the elimination rate constant might be
modeled in terms of rapidly changing serum creatinine.
However, in the data situation at hand, only one dose is
given, and no concomitant variables other than dose and time
are available. So the subject’s PK parameters are
simply elements of
-derivatives are computed
in the PK routine. The typical values of the PK parameters
are just the subject’s values of these parameters. In
principle these could be modeled in terms of concomitant
variables, e.g. the elimination rate constant might be
modeled in terms of rapidly changing serum creatinine.
However, in the data situation at hand, only one dose is
given, and no concomitant variables other than dose and time
are available. So the subject’s PK parameters are
simply elements of  , the
correspondence being exactly the same as that given in the
example in Guide I, section C. Namely, the rate constants of
absorption and elimination are
, the
correspondence being exactly the same as that given in the
example in Guide I, section C. Namely, the rate constants of
absorption and elimination are
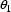 and
and
 , respectively. As in
Example I (section L.1), the scaling parameter of the plasma
compartment is identified with Vd, or
, respectively. As in
Example I (section L.1), the scaling parameter of the plasma
compartment is identified with Vd, or
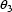 .
.
Since every call to PK with a different event record results in the same output from PK (for fixed THETA), only one call is necessary. Therefore, IDEF(1,2) is set to 1, thereby limiting calls to PK at ICALL=2 to one per data set; see section H.
When the data are from a single subject, and the run involves data simulation, where the simulation and analysis models for PK parameters are the same, PK code at ICALL=4 can be exactly the same as that at ICALL=2. In the example the code in Figure 3 would work just as well when simulation only is implemented, or when estimation only is implemented, or when both simulation and estimation are implemented. When the simulation and analysis models for PK parameters differ, then codes at ICALL=2 and ICALL=4 will simply differ. Structural kinetic differences between simulation and analysis models may be accommodated using an ADVAN implementing one of the general linear or nonlinear models (see chapter VI), or by simulating data in one NONMEM run with one model and analyzing them in another NONMEM run with another model.
This example is similar to Example III, except that a pharmacodynamic observation is recorded at each of ten times, and a simple Emax type model, with the drug concentration being that of an effect compartment, is used. The same kinetic model from Example III is used, with the addition of an effect compartment attached to the central compartment. The purpose of this section is to describe the implementation of these kinetics. The pharmacodynamic model itself, and its implementation, are described in section IV.G.4. In order to implement the kinetics an ADVAN implementing a general linear model is used (although the ADVAN implementing the two compartment linear mammillary model with first order absorption could also be used for these particular kinetics). It is assumed that the PD observations are obtained from the same subject from which the PK observations in Example III are obtained, and that the values of the PK parameters (except for the elimination rate constant from the effect compartment) are those estimates obtained in Example III.
A code for PK is given in Figure 8. (A
corresponding NM-TRAN abbreviated code is shown in Figure 30
as part of an NM-TRAN control stream.) As with Example III,
compartments 1 and 2 are the depot and central compartments,
respectively; compartment 3 is the effect compartment. When
using a general linear model, the numbering of the
compartments is specified in the user-supplied MODEL routine
(see section VI.B). A dummy TRANS routine, TRANS1, that
allows the rate constants to be modeled in PK, is the only
TRANS routine (from the PREDD Library) that is available
with a general linear model (see next section). The
elimination rate constant from the effect compartment is to
be estimated; it is identified with
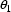 . The rate constant from
the central compartment to the effect compartment is set to
0.1% of the elimination rate constant from the central
compartment, so that the amount in the central compartment
is unaffected by the kinetics of the effect compartment.
Concentration in the effect compartment is not observed, so
the volume in this compartment is not estimable. However, if
the volume changes by a known scale factor s, the
. The rate constant from
the central compartment to the effect compartment is set to
0.1% of the elimination rate constant from the central
compartment, so that the amount in the central compartment
is unaffected by the kinetics of the effect compartment.
Concentration in the effect compartment is not observed, so
the volume in this compartment is not estimable. However, if
the volume changes by a known scale factor s, the
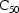 parameter of the Emax model
simply changes by
parameter of the Emax model
simply changes by  .
Therefore, the volume is arbitrary and is often obtained, as
in this example, so to make the concentration the same as
central compartment concentration at steady-state. When
using a general linear model, the numbering of the rate
constants is specified in the user-supplied MODEL routine
(see section VI.B).
.
Therefore, the volume is arbitrary and is often obtained, as
in this example, so to make the concentration the same as
central compartment concentration at steady-state. When
using a general linear model, the numbering of the rate
constants is specified in the user-supplied MODEL routine
(see section VI.B).
Were the data from a population of subjects,
there would be interindividual variability in various
parameters of the model, in particular in the kinetic
parameters. The values of K12, K20, and VD could be set to
subject-specific estimates obtained from analyzing PK data
from each subject separately, as were the values of these
parameters for the subject of this example. The values for a
given subject could be included in his event records and
then would be available to PK in EVTREC. This would account
for the interindividual variability in these parameters. The
elimination rate constant from the effect compartment could
be modeled with an 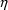 -variable, accounting for random individual variability in
this parameter. The same considerations regarding such
modeling, which have been discussed in previous sections of
this chapter and illustrated in sections L.1 and L.2, apply.
Alternatively, K12, K20, and VD could themselves be modeled
with
-variable, accounting for random individual variability in
this parameter. The same considerations regarding such
modeling, which have been discussed in previous sections of
this chapter and illustrated in sections L.1 and L.2, apply.
Alternatively, K12, K20, and VD could themselves be modeled
with 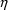 -variables. Then there
are two possibilities. The
-variables. Then there
are two possibilities. The  ’s and
’s and  elements that
are a part of the model for these parameters could be set to
estimates obtained from analyzing PK data. Alternatively,
they, along with the population parameters which are a part
of the pharmacodynamic model, could be estimated by fitting
both PK data and PD data simultaneously.
elements that
are a part of the model for these parameters could be set to
estimates obtained from analyzing PK data. Alternatively,
they, along with the population parameters which are a part
of the pharmacodynamic model, could be estimated by fitting
both PK data and PD data simultaneously.
To compute the kinetic equations for a kinetic model, PREDPP - but more precisely, the chosen ADVAN - uses an internal set of parameters. These parameters may be modeled in PK, but a different set, one preferred by the user, can be modeled there instead. The TRANS subroutine translates (or transforms) the values for a set of basic PK parameters modeled in PK to a set of values for the internal parameters. The PREDPP Library has a number of TRANS subroutines, representing different possible parameterizations, from which the user may choose (see chapter VII). If a suitable translator is not found in the Library, the user may write his own. The form of such a subroutine is described in this section.
For a linear kinetic model, the internal parameters are the microconstants, i.e. rate constants, of the model. For a linear model, other than a general linear model, these parameters are numbered in the same way as the microconstants with TRANS1 from the PREDPP Library (see section VII.C). If the model is a general linear kinetic model, the MODEL subroutine specifies a numbering of these parameters (see section VI.B). For the simple Michaelis-Menton elimination model (see section VII.C.10), the two internal parameters are the same as the first two basic parameters listed for TRANS1, and are numbered the same. The kinetic equations for a general nonlinear kinetic model PREDPP essentially consist of the differential-algebraic equations given by the user in the DES and AES routines to describe the model (see sections VI.C and VI.E). The parameters of these equations comprise the internal set of parameters; they are numbered according to the numbering used in the DES and AES routines.
The preface to TRANS can be
SUBROUTINE TRANS (ITRANS,IRGG,GG,NETAS) DIMENSION GG(IRGG,*) and if double precision NONMEM is used: DOUBLE PRECISION GG
However, if the Laplacian method to be used, then GG should be dimensioned: GG(IRGG,11,*).
The argument ITRANS functions similarly to ICALL in PK. A value of 1 signals to TRANS that it is being called for the first time in the NONMEM problem. A value of 2 signals a regular data analytic call, and a value of 4 signals a regular data simulation call. At ITRANS=1, ITRANS must be reset by TRANS to a number in the range 1-8999. This number appears on NONMEM output, allowing the user to identify the TRANS routine being used. At ITRANS=2 and 4, TRANS must modify values in the GG array.
Suppose P denotes the vector of internal parameters. The user may choose to model instead a vector of parameters R. R may contain more elements than P. Let T be a transformation taking R onto P, i.e. the nth element of P is given by

for some function
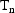 . E.g.
. E.g.
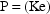 [ADVAN1];
[ADVAN1];
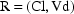 [TRANS2]; and
[TRANS2]; and
 . Then the typical value of
the nth element of P is defined by
. Then the typical value of
the nth element of P is defined by

The first derivative of the nth element of P with
respect to  is
is

The second-partial derivative of the nth element
of P with respect to  ,
,
 is
is

So in terms of the example:


At ITRANS=2, on input the GG array has stored in
it the values computed by PK (except that were any PK
parameter modeled in its logarithm form in PK, PREDPP would
have already exponentiated its typical/subject-specific
value and multiplied its  -derivatives by its exponentiated typical/subject-specific
value). On output the GG array should have stored in it the
values that would be computed by PK were the internal
parameters P modeled directly in PK (and none in their
logarithmic form). So the code for TRANS2, using the above
example, is essentially:
-derivatives by its exponentiated typical/subject-specific
value). On output the GG array should have stored in it the
values that would be computed by PK were the internal
parameters P modeled directly in PK (and none in their
logarithmic form). So the code for TRANS2, using the above
example, is essentially:
GG(1,1) = GG(1,1)/GG(2,1)
IF (ITRANS.EQ.2) THEN
DO 10 K = 1,NETAS
10 GG(1,1+K) = GG(1,1+K)/GG(2,1)-GG(1,1)*GG(2,1+K)/GG(2,1)
ENDIF
if only first derivatives are needed, and is:
A(1) = GG(1,1,1)/GG(2,1,1)
IF (ITRANS.EQ.2) THEN
DO 10 K = 1,NETAS
A(1+K) = GG(1,1+K,1)/GG(2,1,1)
1 -GG(1,1,1)*GG(2,1+K,1)/GG(2,1,1)**2
DO 10 L = 1,K
10 GG(1,1+K,1+L) =
1 -(GG(2,1+K,1)*GG(1,1+L,1)+GG(1,1+K,1)*GG(2,1+L,1)
2 +GG(1,1,1)*GG(2,1+K,1+L))/GG(2,1,1)**2
3 +2*GG(1,1,1)*GG(2,1+K,1)*GG(2,1+L,1)/GG(2,1,1)**3
4 +GG(1,1+K,1+L)/GG(2,1,1)
DO 20 K = 1,NETAS
20 GG(1,1+K,1)=A(1+K)
ENDIF
GG(1,1,1)=A(1)
if first and second derivatives are needed. Note
that the total number of 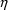 variables used in the problem is given in the last argument
of TRANS and can be used as illustrated here.
variables used in the problem is given in the last argument
of TRANS and can be used as illustrated here.
At ITRANS=4, on input the GG array has stored in its first column the values of the subject-specific PK parameters computed by PK (except that for each subject-specific PK parameter modeled in its logarithm form in PK, PREDPP has already exponentiated its value). On output the GG array should have stored in its first column the values that would be computed by PK were the internal parameters P modeled directly in PK (and none in their logarithmic form). Since, when ITRANS=4, only the first column of the GG array is relevant, computations involving other columns may be skipped, as in the above code.
TRANS has access to the entire GG array,
including the typical/subject-specific values and
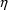 -derivatives of the
additional PK parameters. It can therefore perform a
translation for all parameters, including scaling
parameters, bioavailability fractions, etc., not just for
the basic PK parameters. This type of translation, however,
is usually not needed.
-derivatives of the
additional PK parameters. It can therefore perform a
translation for all parameters, including scaling
parameters, bioavailability fractions, etc., not just for
the basic PK parameters. This type of translation, however,
is usually not needed.
TOP
TABLE OF CONTENTS
NEXT CHAPTER ...