NONMEM Users Guide Part VI - PREDPP - Chapter VI
VI. Other User Subroutines
VI.A. INFN
VI.B. MODEL
VI.C. DES
VI.D. TOL
VI.E. AES
NONMEM Users Guide Part VI - PREDPP - Chapter VI
VI. Other User Subroutines
VI.A. INFN
There is an INFN routine supplied on the NONMEM
distribution medium that must be linked with the other
routines for a NONMEM-PREDPP load module; see section VII.A.
It is a "dummy" routine; it does nothing. It may
be replaced by a user-supplied INFN routine that allows the
user to carry out any of his own programmed computations at
both the beginning of a problem and again, at the ending of
the problem. At the beginning of the problem PREDPP calls
INFN -- the initialization call
and at the ending of the problem PREDPP calls
INFN -- the finalization call
At each call, the user has read-write access to
his data via use of the NONMEM utility routine PASS
described in Guide II. Thus data can be transgenerated, and
additional data items can be produced at both the beginning
and ending of a problem. Since the finalization call
actually occurs before the Table and Scatterplot Steps, new
data items generated by INFN at this call can be tabled and
scatterplotted.
The preface to INFN must be
SUBROUTINE INFN (ICALL,THETA,DATREC,INDXS,NEWIND)
DIMENSION THETA(*),DATREC(*),INDXS(*)
and if double precision NONMEM is used:
DOUBLE PRECISION THETA
The argument ICALL is 1 or 3, according to
whether the call to INFN is the initialization or
finalization call. A value ICALL=0 indicates that the call
is a special one occuring before the initialization call of
problem 1, allowing initialization to take place in a
multiple problem run.
The arguments THETA and DATREC function just as
they do in any PRED routine when the argument ICALL is 0, 1,
or 3. In particular, when ICALL=1, THETA is the array of
initial estimates of  for the
problem, and when ICALL=3, THETA is the array of final
estimates of
for the
problem, and when ICALL=3, THETA is the array of final
estimates of  for the
problem. When ICALL=0, THETA is the array of initial
estimates of
for the
problem. When ICALL=0, THETA is the array of initial
estimates of  for problem 1.
When ICALL=1 or 3, the DATREC array initially contains the
first data record of the data set for the problem, but using
PASS, the contents of DATREC are replaced by other data
records of the data set for the problem. (When ICALL=0,
DATREC is initially the first data record of the data set
for problem 1, but using PASS, the contents of DATREC are
replaced by other data records for problem 1.)
for problem 1.
When ICALL=1 or 3, the DATREC array initially contains the
first data record of the data set for the problem, but using
PASS, the contents of DATREC are replaced by other data
records of the data set for the problem. (When ICALL=0,
DATREC is initially the first data record of the data set
for problem 1, but using PASS, the contents of DATREC are
replaced by other data records for problem 1.)
The user should not use PASS to modify either the
ID or MDV data items.
An initialization call can be used for any sort
of initialization. For example, user-arrays in the routines
PK and ERROR can be initialized if these arrays are stored
in a common block declared in INFN. Also, interpolated
values of a concomitant variable can be computed for event
records in which values are missing, e.g. other-type event
records that have been included so that predictions can be
obtained at the times in these records. This could also be
done in PK or ERROR, but then this would be done with
every call to these routines; if done in INFN, the
computation is done once only.
An example of a user-supplied INFN routine is
given in Figure 37. This INFN routine can be used to obtain
linearly interpolated values of an independent variable V
for those event records in which a value is missing. Simple
linear interpolation may not be adequate for all data
situations. With this INFN it is assumed that there is one
data record per event record. It is also assumed that each
individual record has no fewer than 2 event records with
measured values of V and that every event record has a data
item which the user might call the missing independent
variable data item (which assumes values defined in the
comment statements of the code). The routine uses PASS to
pass through the data twice: once, to store all pairs of
values for time and V from event records with measured
values of V, and again, to store the interpolated values in
records with missing values of V.
The one-dimensional array, INDXS, functions in
the way described in Guide I, section C.4.1. The user places
integers into this array, using the INDEX control record.
These integers are then available to PREDPP and therefore to
INFN. For further details see section III.C where the use of
INDXS is illustrated with subroutine PK.
INFN also has access to an argument NEWIND. This
variable changes value during a pass through the data using
PASS. NEWIND is an integer variable acting like the NEWIND
variable described in Guide I. It assumes one of 3 values: 0
if the data record is the first of the entire data set, 1 if
the data record is the first data record of an individual
record (other than the first individual record), and 2 if
the data record is other than the first data record of an
individual record. (A description of individual records with
single-subject data is given in chapter II.)
The finalization call can use the NONMEM utility
routine GETETA to obtain conditional estimates of the
 ’s (see section
III.E.2). When used in conjunction with PASS, the values
returned for the
’s (see section
III.E.2). When used in conjunction with PASS, the values
returned for the 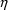 ’s
with each call to GETETA are appropriate for the individual
whose data record is currently in DATREC.
’s
with each call to GETETA are appropriate for the individual
whose data record is currently in DATREC.
VI.B. MODEL
Some ADVAN routines, specifically those
implementing general linear or nonlinear kinetic models,
require an additional user-supplied routine called MODEL
which allows the user to conveniently specify important
aspects of the model. MODEL is called once only, at the
beginning of a NONMEM-PREDPP run. Its preface is
SUBROUTINE MODEL (IDNO,NCM,NPAR,IR,IATT,LINK)
DIMENSION IATT(IR,*),LINK(IR,*)
The user may have several MODEL routines and use
different ones for different runs. The routine used in a
particular run can be identified from the output. For this
to happen, an integer identification value should be
assigned by MODEL to the variable IDNO. This value will be
printed on the first PREDPP problem summary
page.
The total number of compartments to be used,
excluding the output compartment, is specified by assigning
this number to NCM. This number cannot exceed 9.
Basic PK parameters exist for general linear and
nonlinear models as they do for more specific models. A
TRANS routine is used which translates the set of basic PK
parameters whose values are computed in the PK routine to a
set of parameters used internally by the ADVAN routine. The
maximum number of basic PK parameters to be used in any
TRANS routine ( 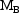 ; see
section III.G) is specified by assigning this number to the
variable NPAR. The maximum number of basic PK parameters
plus the number of additional parameters whose row indices
are given explicitly in PK (at ICALL=1) cannot exceed
30.
; see
section III.G) is specified by assigning this number to the
variable NPAR. The maximum number of basic PK parameters
plus the number of additional parameters whose row indices
are given explicitly in PK (at ICALL=1) cannot exceed
30.
Values of compartment attributes must be given
for each compartment (other than the output compartment, for
which these values are fixed by PREDPP; see below). There
are 5 required attributes; one should choose a value for
each of these attributes for each compartment. To choose
these values for the Ith compartment first answer these 5
defining questions:

Values of attributes are given by assigning values to
IATT. IATT is a two-dimensional array of 4 byte integers. If
the answer to the Jth question for compartment I is
’yes’, then set IATT(I,J)=1; if the answer is
’no’, then set IATT(I,J)=0.
There is really no reason for answering ’no’
to question 3 for compartment I other than to activate a
check for dose and reset-dose event records with CMT data
item equal to I. Similarly, the only reason for answering
’no’ to question 2 for compartment I is to
activate a check for other and reset event records with CMT
data item equal to -I. If the Ith compartment is an
equilibrium compartment (see below), then the answer to
question 3 must be ’no’; one cannot put a dose
into an equilibrium compartment.
Labels for the various compartments should also be
given. Labels are displayed in the PREDPP problem summary;
see the Compartment Attributes Table, under column heading
FUNCTION (the label ’OUTPUT’ is supplied by
PREDPP). For example, see Figure 28. A label consists of 8
characters, including blanks. There are two ways to give
these labels.
The first is to include character data in IATT. For
compartment I, the first 4 characters of its label are
stored in IATT(I,6), and the last 4 characters are stored in
IATT(I,7). To store 4 characters in a 4 byte integer
variable, one can store these characters in a 4 byte
character string equivalenced to the 4 byte integer
variable. An alternative, perhaps simpler, way to store the
characters in IATT is to use hollerith data in a DATA
statement as illustrated in Figures 38 and 39 (see
below).
The second is to include character data in a character
array, NAME, listed in a PREDPP common PRNAME. This avoids a
warning error from the FORTRAN compiler which can occur with
some compilers when (as with the first method for giving
labels) character data are stored in integer variables. The
appropriate declarations are:
COMMON /PRNAME/ NAME(10)
CHARACTER*8 NAME
The label for compartment I is stored in NAME(I),
e.g.
NAME(2)=’CENTRAL’
Unless some nonblank label is stored in NAME, PREDPP
takes the labels from IATT.
The attributes for the output compartment are fixed by
PREDPP: initial status off; no doses allowed; may be turned
on and off; is neither the default observation nor default
dose compartment.
Figure 38 is an example of a MODEL routine that can be
used to describe the one compartment linear model with first
order absorption, just as this model is described in section
VII.C.2. Figure 39 is an example of a MODEL routine that can
be used to describe the three compartment linear model used
with the Example IV developed in sections III.L.4, IV.G.4,
and V.L.4. Both of these routines illustrate the use of the
LINK argument which is discussed below. (An NM-TRAN $MODEL
record corresponding to the MODEL routine of Figure 39 is
shown in Figure 30 as part of an NM-TRAN control stream. The
information in the MODEL routine which is not explicitly
specified in the $MODEL record is obtained from the $PK
record.)
Most pharmacokinetic models involve only nonequilibrium
compartments, compartments such that the amounts of drug in
them can be given by a solution to a system of differential
equations. However, one ADVAN routine - ADVAN9 - allows a
model (a general nonlinear model) to be comprised of both
nonequilibrium and equilibrium compartments. Equilibrium
compartments are, roughly speaking, compartments such that
at any time the amounts of drug in them can be given by a
solution to a system of algebraic equations.
There are two additional attributes to which values must
be given only when ADVAN9 is used. The first of these simply
identifies the compartment as an equilibrium compartment or
not. The second of these relates to the output compartment.
The amount of drug in the output compartment at time t is
given by A+B-C, where A is the total amount in the system at
s, the time the compartment is turned on, B is the total
amount of drug input to the system between times s and t,
and C is the total amount in the system at time t. If an
equilibrium compartment represents a subcompartment, i.e.
the amount D of drug in the compartment is part of the
amount of drug in another compartment, D should be excluded
from A and C. The attribute in question is concerned with
whether D should or should not be excluded from A and C. To
choose values for the two attributes for the Ith compartment
first answer:
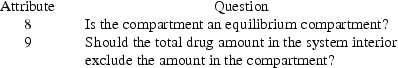
If the answer to the Jth question (J=8,9) for
compartment I is ’yes’, then set IATT(I,J)=1; if
the answer is ’no’, then set IATT(I,J)=0.
The internal parameters of a general linear model are
the rate constants. The user assigns each rate constant a
number, any number between 1 and the value assigned to NPAR.
The numbering is established using the LINK array.
LINK is a two-dimensional integer array. If no drug can
distribute from the Ith compartment to the Jth compartment,
then one can assign 0 to LINK(I,J), or not bother assigning
any value to LINK(I,J). In particular, LINK(I,I) should
always be ignored. If drug can distribute from the Ith
compartment to the Jth compartment, then one assigns to
LINK(I,J) the number of the rate constant quantifying this
(first-order) distribution. The LINK array should, in
particular, account for the distribution of drug from
compartment I to the output compartment. That is, if such
distribution can take place, then a number should be
assigned to LINK(I,NCM+1). The numbers of the rate constants
need not start with the number 1, and they need not be
consecutive, i.e. numbers may be skipped. Moreover, two rate
constants can be assigned the same number; this forces their
values and 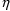 -derivatives to
be the same.
-derivatives to
be the same.
With a general nonlinear model the user explicitly
specifies a set of differential equations (see section C).
These equations are parameterized in terms a set of internal
kinetic parameters. The LINK array plays no role with a
general nonlinear model. The internal parameters are
numbered between 1 and the number assigned to NPAR. The
rules concerning internal parameter numbering are the same
as given above for rate constant numbering.
VI.C. DES
This user-supplied subroutine is required by a general
nonlinear model. Also, regardless of the model chosen, it is
also required whenever the user chooses to compute
steady-state kinetics using the SS6 routine; see section
VII.B. Usually, though, SS6 is only used when steady-state
kinetics are computed with a general nonlinear model, so
that DES would be required in any event. (When the model is
not a general nonlinear model and SS6 is used, then unless
steady-state infusions are present in the data set, the only
executable statement in DES need be: RETURN.)
DES allows the user to conveniently specify the system
of ordinary differential equations describing the underlying
kinetics (of the nonequilibrium compartments; see section
B). Its preface is
SUBROUTINE DES (A,P,T,DADT,IR,DA,DP)
DIMENSION A(*),P(*),DADT(*),DA(IR,*),DP(IR,*)
and if double precision NONMEM is used:
DOUBLE PRECISION A,P,T,DADT,DA,DP
The system of differential equations can be expressed
mathematically by

where A is the vector of drug amounts in all the
various compartments (other than the output compartment), P
is the vector of internal PK parameters (see section B.) , t
is time, and n is the number of compartments (excluding the
output compartment and all equilibrium compartments; see
section B). The parameter 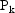 is defined to be the kth internal parameter. It is a
continuously acting parameter. An example of such a system
is this.
is defined to be the kth internal parameter. It is a
continuously acting parameter. An example of such a system
is this.




i.e. the familiar one compartment model with linear
elimination and absorption from a drug depot. In general the
system need not be linear, or even homogeneous (i.e. the h
functions can depend on t).
The arguments A, P, and T of DES are inputs to the
routine and correspond to A, P, and t in (1). T is a
"continuously-valued" variable, not the
discretely-valued time data item. The primary task of DES is
to compute the values of the h functions and store these
values in DADT. The value of
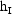 is stored in DADT(I).
is stored in DADT(I).
In addition to computing the values of the
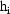 , DES must also compute the
values
, DES must also compute the
values
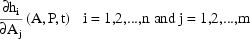
where m is the number of all compartments, including
equilibrium compartments should they exist (see section
B). With population data DES must also compute the
values
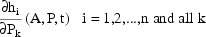
The value of 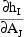 is stored
in DA(I,J), and the value of
is stored
in DA(I,J), and the value of
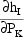 is stored in DP(I,K). In
the above example:
is stored in DP(I,K). In
the above example:
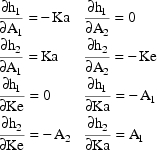
A routine for implementing the example is given in
Figure 40. The numbering of the compartments is that
specified by the MODEL routine given in Figure 38. Since the
LINK array plays no role with a general nonlinear model, the
numbers set in the LINK array are ignored. Note that it is
unnecessary to set 0’s in either DA or DP.
We emphasize that it is only necessary for the
computations in DES to characterize the underlying kinetics.
These computations are not to be concerned with matters of
boundary conditions or drug input functions. Those matters
are handled by PREDPP itself.
A value stored in a variable (or array element) V in DES
may be displayed in a table or scatterplot. To accomplish
this, common NMPRD4 must be included in DES, and V must be
listed in NMPRD4. However, there is rarely a need to do
this. The matter is complicated by the fact that multiple
calls to DES are associated with each event record. More
information about the display of DES-defined items may be
obtained by consultation with the NONMEM Project Group.
Common NMPRD4 also provides a convenient place to store
values of variables to be shared between DES and other user
routines, and it is used thusly when these routines are
generated from NM-TRAN abbreviated code (see Guide IV).
VI.D. TOL
This user-supplied subroutine is required when using an
ADVAN or SS routine that uses numerical techniques. These
are the general nonlinear models (ADVAN6,8,9), the one
compartment model with Michaelis-Menten elimination
(ADVAN10), and two particular steady-state routines (SS6,9);
see section VII.C Its preface is
SUBROUTINE TOL(NRD)
DIMENSION NRD(*)
The purpose of TOL is to set NRD(I) to the number of
accurate digits that are required in the computation of the
drug amount in compartment I, i.e. the relative
tolerance ADVAN9 has the capability of using different
values of NRD for different compartments. However, all the
other ADVAN and SS routines requiring TOL take the relative
tolerance to be the same for all compartments; NRD(I),
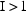 , is ignored, and only
NRD(1) is used. Even with ADVAN9 the accuracy of a
steady-state amount (computed by SS9) for compartment
, is ignored, and only
NRD(1) is used. Even with ADVAN9 the accuracy of a
steady-state amount (computed by SS9) for compartment
 ,
,
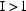 , is only controlled to be
NRD(1) digits. The user will usually be content with a
single relative tolerance which applies to all compartments.
In this case, as a rule of thumb, one should begin by
setting NRD(1) to n+1 or n+2, where n is the number of
significant digits required in the parameter estimates, or
with double precision, perhaps to n+2 or n+3. If one
succeeds with this setting, one might try increasing NRD
slightly.
, is only controlled to be
NRD(1) digits. The user will usually be content with a
single relative tolerance which applies to all compartments.
In this case, as a rule of thumb, one should begin by
setting NRD(1) to n+1 or n+2, where n is the number of
significant digits required in the parameter estimates, or
with double precision, perhaps to n+2 or n+3. If one
succeeds with this setting, one might try increasing NRD
slightly.
Indeed, NRD can be a scalar, rather than an array
appearing in a DIMENSION statement, in which case NRD is
simply assigned a unique relative tolerance. Even with
ADVAN9 this is true.
An example of a TOL routine is given in Figure 41.
VI.E. AES
This user-supplied subroutine is required by a general
nonlinear model with equilibrium compartments (i.e. ADVAN9).
AES allows the user to conveniently specify the system of
algebraic equations describing the underlying kinetics of
the equilibrium compartments. Its preface is
SUBROUTINE AES (INIT,A,P,T,E,IR,DA,DP,DT)
DIMENSION A(*),P(*),E(*),DA(IR,*),DP(IR,*),DT(*)
and if double precision NONMEM is used:
DOUBLE PRECISION A,P,T,E,DA,DP,DT
The system of algebraic equations is actually part of a
coupled system of differential and algebraic
equations describing the underlying kinetics of all the
compartments, equilibrium and nonequilibrium compartments.
This coupled system can be expressed mathematically by

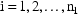


where A is the vector of drug amounts in all the
various compartments (other than the output compartment), P
is the vector of internal PK parameters, t is time,
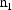 is the number of
nonequilibrium compartments (excluding the output
compartment), and
is the number of
nonequilibrium compartments (excluding the output
compartment), and 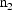 is the
number of equilibrium compartments. The parameter
is the
number of equilibrium compartments. The parameter
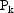 is defined to be the kth
internal parameter. It is a continuously acting parameter. A
very simple example is this.
is defined to be the kth
internal parameter. It is a continuously acting parameter. A
very simple example is this.
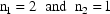
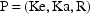


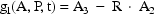
i.e. the familiar one compartment model with linear
elimination and absorption from a drug depot, but where a
third compartment is in equilibrium with the central
compartment. The parameter R is a ratio of drug amounts, not
a rate parameter. In general the system need not be linear,
or even homogeneous (i.e. the h and g functions can depend
on t).
The arguments A, P, and T of AES are inputs to the
routine and correspond to A, P, and t in (2) and (3). The
primary task of AES is to compute the values of the g
functions and store these values in E. The value of
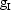 is stored in E(
is stored in E(
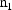 +I). The values of the h
functions are computed and stored by the DES subroutine (see
section C).
+I). The values of the h
functions are computed and stored by the DES subroutine (see
section C).
In addition to computing the values of the
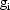 , AES must also compute the
values
, AES must also compute the
values
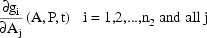
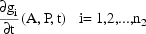
With population data AES must also compute the
values

The value of  is stored
in DA(
is stored
in DA(  +I,J), the value of
+I,J), the value of
 is stored in DP(
is stored in DP(
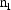 +I,K), and the value of
+I,K), and the value of
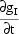 is stored in DT(
is stored in DT(
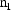 +I).
+I).
When INIT=0, this signals a regular call to AES in which
the values of the g functions must be stored in E and the
partial derivatives just enumerated must be stored in DA,
DP, and DT. Such a call occurs with many different values of
time over an integration interval, although the g functions
usually do not depend on time. When INIT=1, this signals an
initial-condition call to AES. Such a call occurs
only with that value of time,
 , coinciding with the
beginning of an integration interval, and at such a call
values that hold for A at
, coinciding with the
beginning of an integration interval, and at such a call
values that hold for A at 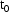 ,
for the equilibrium compartments, must be stored in A. (No
partial derivatives need be stored.) These values are used
as initial conditions for the integration. Usually, these
values have already been obtained by ADVAN9, and an
initial-condition call is unnecessary and does not occur.
However, when, for example,
,
for the equilibrium compartments, must be stored in A. (No
partial derivatives need be stored.) These values are used
as initial conditions for the integration. Usually, these
values have already been obtained by ADVAN9, and an
initial-condition call is unnecessary and does not occur.
However, when, for example, 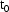 is a time at which a bolus dose is given (such a dose must
go into a nonequilibrium compartment), then an
initial-condition call is necessary. At an initial-condition
call, the values for A at
is a time at which a bolus dose is given (such a dose must
go into a nonequilibrium compartment), then an
initial-condition call is necessary. At an initial-condition
call, the values for A at 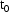 ,
for the nonequilibrium compartments, are available. Values
for P are also available. (Let
,
for the nonequilibrium compartments, are available. Values
for P are also available. (Let
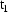 be the end of the
integration interval. Both
be the end of the
integration interval. Both 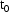 and
and 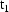 are state times; see
section III.B.2. The values for P are computed from the
information in the argument record associated with
are state times; see
section III.B.2. The values for P are computed from the
information in the argument record associated with
 , and, if
, and, if
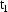 is a nonevent dose time,
also from the information in the record describing the
dose.) Therefore, in principle the system of algebraic
equations given by (3) can be solved for the amounts in the
equilibrium compartments at
is a nonevent dose time,
also from the information in the record describing the
dose.) Therefore, in principle the system of algebraic
equations given by (3) can be solved for the amounts in the
equilibrium compartments at 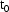 , although, obtaining an explicit solution may not be
possible. However, only an approximate solution is actually
needed at INITI=1. If only approximate values for A are
computed at an initial-condition call, rather than exact
values, then INIT itself should be reset to 0 in AES. These
approximate values serve as an initial solution, and a more
precise solution is obtained numerically by ADVAN9. The
number of accurate digits in the final solution with respect
to all equilibrium compartments will be the number
given in NRD(1) by subroutine TOL (see section D). If at
INIT=1 a solution is returned that is at least as accurate
as this, then the value of INIT should be left unchanged,
i.e. INIT=1.
, although, obtaining an explicit solution may not be
possible. However, only an approximate solution is actually
needed at INITI=1. If only approximate values for A are
computed at an initial-condition call, rather than exact
values, then INIT itself should be reset to 0 in AES. These
approximate values serve as an initial solution, and a more
precise solution is obtained numerically by ADVAN9. The
number of accurate digits in the final solution with respect
to all equilibrium compartments will be the number
given in NRD(1) by subroutine TOL (see section D). If at
INIT=1 a solution is returned that is at least as accurate
as this, then the value of INIT should be left unchanged,
i.e. INIT=1.
In the above example:
Also, at an initial-condition call
 can be given by
can be given by

A routine for implementing the example is given in
Figure 42. The numbering of the compartments and the
parameters is that specified by the MODEL routine given in
Figure 43, which is an extension of the MODEL routine given
in Figure 38. (Note though, that the LINK array plays no
role with a general nonlinear model, and no values in this
array are set in the routine of Figure 43.) The DES
subroutine shown in Figure 40 can be used with this example.
Note that it is unnecessary to set 0’s in either DA,
DP, or DT.
A value stored in a variable (or array element) V in AES
may be displayed in a table or scatterplot. To accomplish
this, common NMPRD4 must be included in AES, and V must be
listed in NMPRD4. However, there is rarely a need to do
this. The matter is complicated by the fact that multiple
calls to AES are associated with each event record. More
information about the display of AES-defined items may be
obtained by consultation with the NONMEM Project Group.
Common NMPRD4 also provides a convenient place to store
values of variables to be shared between AES and other user
routines, and it is used thusly when these routines are
generated from NM-TRAN abbreviated code (see Guide IV).
TOP
TABLE OF CONTENTS
NEXT CHAPTER ...
 for the
problem, and when ICALL=3, THETA is the array of final
estimates of
for the
problem, and when ICALL=3, THETA is the array of final
estimates of  for the
problem. When ICALL=0, THETA is the array of initial
estimates of
for the
problem. When ICALL=0, THETA is the array of initial
estimates of  for problem 1.
When ICALL=1 or 3, the DATREC array initially contains the
first data record of the data set for the problem, but using
PASS, the contents of DATREC are replaced by other data
records of the data set for the problem. (When ICALL=0,
DATREC is initially the first data record of the data set
for problem 1, but using PASS, the contents of DATREC are
replaced by other data records for problem 1.)
for problem 1.
When ICALL=1 or 3, the DATREC array initially contains the
first data record of the data set for the problem, but using
PASS, the contents of DATREC are replaced by other data
records of the data set for the problem. (When ICALL=0,
DATREC is initially the first data record of the data set
for problem 1, but using PASS, the contents of DATREC are
replaced by other data records for problem 1.) ’s (see section
III.E.2). When used in conjunction with PASS, the values
returned for the
’s (see section
III.E.2). When used in conjunction with PASS, the values
returned for the  ’s
with each call to GETETA are appropriate for the individual
whose data record is currently in DATREC.
’s
with each call to GETETA are appropriate for the individual
whose data record is currently in DATREC. ; see
section III.G) is specified by assigning this number to the
variable NPAR. The maximum number of basic PK parameters
plus the number of additional parameters whose row indices
are given explicitly in PK (at ICALL=1) cannot exceed
30.
; see
section III.G) is specified by assigning this number to the
variable NPAR. The maximum number of basic PK parameters
plus the number of additional parameters whose row indices
are given explicitly in PK (at ICALL=1) cannot exceed
30.
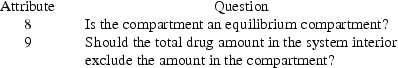
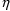 -derivatives to
be the same.
-derivatives to
be the same.
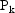 is defined to be the kth internal parameter. It is a
continuously acting parameter. An example of such a system
is this.
is defined to be the kth internal parameter. It is a
continuously acting parameter. An example of such a system
is this.



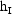 is stored in DADT(I).
is stored in DADT(I).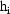 , DES must also compute the
values
, DES must also compute the
values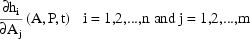
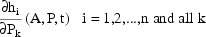
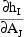 is stored
in DA(I,J), and the value of
is stored
in DA(I,J), and the value of
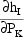 is stored in DP(I,K). In
the above example:
is stored in DP(I,K). In
the above example: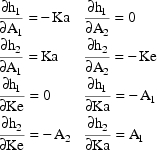
 , is ignored, and only
NRD(1) is used. Even with ADVAN9 the accuracy of a
steady-state amount (computed by SS9) for compartment
, is ignored, and only
NRD(1) is used. Even with ADVAN9 the accuracy of a
steady-state amount (computed by SS9) for compartment
 ,
,
 , is only controlled to be
NRD(1) digits. The user will usually be content with a
single relative tolerance which applies to all compartments.
In this case, as a rule of thumb, one should begin by
setting NRD(1) to n+1 or n+2, where n is the number of
significant digits required in the parameter estimates, or
with double precision, perhaps to n+2 or n+3. If one
succeeds with this setting, one might try increasing NRD
slightly.
, is only controlled to be
NRD(1) digits. The user will usually be content with a
single relative tolerance which applies to all compartments.
In this case, as a rule of thumb, one should begin by
setting NRD(1) to n+1 or n+2, where n is the number of
significant digits required in the parameter estimates, or
with double precision, perhaps to n+2 or n+3. If one
succeeds with this setting, one might try increasing NRD
slightly.
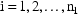


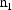 is the number of
nonequilibrium compartments (excluding the output
compartment), and
is the number of
nonequilibrium compartments (excluding the output
compartment), and 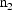 is the
number of equilibrium compartments. The parameter
is the
number of equilibrium compartments. The parameter
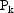 is defined to be the kth
internal parameter. It is a continuously acting parameter. A
very simple example is this.
is defined to be the kth
internal parameter. It is a continuously acting parameter. A
very simple example is this.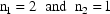
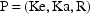


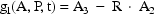
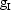 is stored in E(
is stored in E(
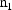 +I). The values of the h
functions are computed and stored by the DES subroutine (see
section C).
+I). The values of the h
functions are computed and stored by the DES subroutine (see
section C).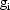 , AES must also compute the
values
, AES must also compute the
values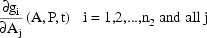
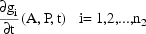

 is stored
in DA(
is stored
in DA(  +I,J), the value of
+I,J), the value of
 is stored in DP(
is stored in DP(
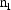 +I,K), and the value of
+I,K), and the value of
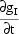 is stored in DT(
is stored in DT(
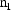 +I).
+I). , coinciding with the
beginning of an integration interval, and at such a call
values that hold for A at
, coinciding with the
beginning of an integration interval, and at such a call
values that hold for A at 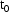 ,
for the equilibrium compartments, must be stored in A. (No
partial derivatives need be stored.) These values are used
as initial conditions for the integration. Usually, these
values have already been obtained by ADVAN9, and an
initial-condition call is unnecessary and does not occur.
However, when, for example,
,
for the equilibrium compartments, must be stored in A. (No
partial derivatives need be stored.) These values are used
as initial conditions for the integration. Usually, these
values have already been obtained by ADVAN9, and an
initial-condition call is unnecessary and does not occur.
However, when, for example, 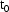 is a time at which a bolus dose is given (such a dose must
go into a nonequilibrium compartment), then an
initial-condition call is necessary. At an initial-condition
call, the values for A at
is a time at which a bolus dose is given (such a dose must
go into a nonequilibrium compartment), then an
initial-condition call is necessary. At an initial-condition
call, the values for A at 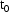 ,
for the nonequilibrium compartments, are available. Values
for P are also available. (Let
,
for the nonequilibrium compartments, are available. Values
for P are also available. (Let
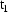 be the end of the
integration interval. Both
be the end of the
integration interval. Both 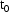 and
and 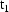 are state times; see
section III.B.2. The values for P are computed from the
information in the argument record associated with
are state times; see
section III.B.2. The values for P are computed from the
information in the argument record associated with
 , and, if
, and, if
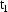 is a nonevent dose time,
also from the information in the record describing the
dose.) Therefore, in principle the system of algebraic
equations given by (3) can be solved for the amounts in the
equilibrium compartments at
is a nonevent dose time,
also from the information in the record describing the
dose.) Therefore, in principle the system of algebraic
equations given by (3) can be solved for the amounts in the
equilibrium compartments at 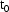 , although, obtaining an explicit solution may not be
possible. However, only an approximate solution is actually
needed at INITI=1. If only approximate values for A are
computed at an initial-condition call, rather than exact
values, then INIT itself should be reset to 0 in AES. These
approximate values serve as an initial solution, and a more
precise solution is obtained numerically by ADVAN9. The
number of accurate digits in the final solution with respect
to all equilibrium compartments will be the number
given in NRD(1) by subroutine TOL (see section D). If at
INIT=1 a solution is returned that is at least as accurate
as this, then the value of INIT should be left unchanged,
i.e. INIT=1.
, although, obtaining an explicit solution may not be
possible. However, only an approximate solution is actually
needed at INITI=1. If only approximate values for A are
computed at an initial-condition call, rather than exact
values, then INIT itself should be reset to 0 in AES. These
approximate values serve as an initial solution, and a more
precise solution is obtained numerically by ADVAN9. The
number of accurate digits in the final solution with respect
to all equilibrium compartments will be the number
given in NRD(1) by subroutine TOL (see section D). If at
INIT=1 a solution is returned that is at least as accurate
as this, then the value of INIT should be left unchanged,
i.e. INIT=1.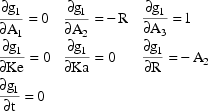
 can be given by
can be given by