NONMEM Users Guide Part VII - Conditional Estimation Methods - Chapter III
III. Usage Guidelines
III.A. Background
III.B. Model Form
III.C. Role of the FO Method
III.D. Role of Centering Methods
III.E. Role of the Hybrid Method
III.F. Problems
NONMEM Users Guide Part VII - Conditional Estimation Methods - Chapter III
III. Usage Guidelines
III.A. Background
Many data sets (real and simulated) have been
examined using the first-order (FO) estimation method and,
more recently, the conditional estimation methods. With many
population pharmacokinetic data sets, the FO method works
fairly well. It requires far less CPU time than does a
conditional estimation method. However, from the time of its
earliest usage there has been a small number of examples
where the method has not worked adequately. Evidence
suggesting that the method may not be adequate with a
particular data set can be readily obtained with the
goodness-of-fit scatterplot: with mean-variance
intraindividual models, a plot of observations versus
(population) predictions. Consider two such scatterplots in
Figures 1 and 2. The one in Figure 1, resulting from use of
the FO method, shows a clear bias in the fit. The data
result from single oral bolus doses being given to a number
of subjects; the data are modeled with a two compartment
linear model with first-order absorption from a drug depot.
The scatterplot in Figure 2 results from use of the FOCE
method without interaction. Much of the bias is eliminated
with the use of this method. In this situation, the benefit
from the extra expenditure of computer time that is needed
with the method is substantial.
The Laplacian method can use considerably more
computer time than the FOCE method, depending on the
complexity of the computations for obtaining needed second
derivatives. In this example, the extra expenditure of
computer time needed with the Laplacian method is not much,
but the benefit is also not much. The scatterplot resulting
from using the Laplacian method is very similar to that of
Figure 2.
The Laplacian method should perform no worse than
the FOCE method (the former avoids the first-order
approximation). The FOCE method should perform no worse than
the FO method (the adaquacy of the first-order approximation
is better when the 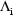 are
evaluated at the conditional estimates, rather than at 0).
Similarly, the hybrid method should also perform no worse
than the FO method, but perhaps not as well as the FOCE
method. (See e.g. Figure 3, which is the goodness-of-fit
plot for the same data described above, using the hybrid
method (with two out of four
are
evaluated at the conditional estimates, rather than at 0).
Similarly, the hybrid method should also perform no worse
than the FO method, but perhaps not as well as the FOCE
method. (See e.g. Figure 3, which is the goodness-of-fit
plot for the same data described above, using the hybrid
method (with two out of four 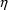 ’s "zeroed".)) This defines a type of
hierarchy to the methods.
’s "zeroed".)) This defines a type of
hierarchy to the methods.
The need to proceed up the hierarchy from the FO
method increases as the degree to which the intraindividual
models are nonlinear in the  increases. The need to use the Laplacian method increases
because as the degree of nonlinearity increases, the
adequacy of the first-order approximation decreases. The
need to use the FOCE method increases because as the degree
of nonlinearity increases, the adequacy of the first-order
approximation depends more on the values at which the
increases. The need to use the Laplacian method increases
because as the degree of nonlinearity increases, the
adequacy of the first-order approximation decreases. The
need to use the FOCE method increases because as the degree
of nonlinearity increases, the adequacy of the first-order
approximation depends more on the values at which the
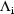 are evaluated.
are evaluated.
Population (structurally) linear pharmacokinetic
models are often rather linear (as just defined), although
the degree of nonlinearity increases with the degree of
multiple dosing. With these models the Laplacian method is
rarely, if ever, needed. With simple bolus dosing, the FOCE
method is often not needed, although the example cited above
serves as a reminder not to interpret this last assertion
too optimistically. On the other hand, population nonlinear
pharmacokinetic models (e.g. models with Michaelis-Menten
elimination) can be quite nonlinear. Population
pharmacodynamic models also can be quite nonlinear, and
especially with models for categorical- and
discrete-ordinal-type observations, the Laplacian method is
invariably the best choice.
The ability of a conditional estimation method to
produce results different from those obtained with the FO
method decreases as the degree of random interindividual
variablity, i.e. "the size" of
 decreases. This is because
the conditional methods use conditional estimates of the
decreases. This is because
the conditional methods use conditional estimates of the
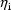 , which are all shrunken to
0, and the shrinkage is greater the smaller the size of
, which are all shrunken to
0, and the shrinkage is greater the smaller the size of
 . The value 0 is the value
used for the
. The value 0 is the value
used for the 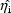 with the FO
method. Similarly, the ability of FOCE to produce results
different from those obtained with the hybrid method
decreases as the degree of random interindividual
variablity, i.e. "the size" of
with the FO
method. Similarly, the ability of FOCE to produce results
different from those obtained with the hybrid method
decreases as the degree of random interindividual
variablity, i.e. "the size" of
 decreases. In fact, suppose
one tries to use the FOCE method and finds that some
estimates of interindividual variances are rather large
compared to others. Then using the hybrid method where those
elements of
decreases. In fact, suppose
one tries to use the FOCE method and finds that some
estimates of interindividual variances are rather large
compared to others. Then using the hybrid method where those
elements of 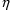 with small
variance are "zeroed", may well result in a fit
about as good as that using FOCE (in contrast to that shown
in Figure 3), and if the number of elements of
with small
variance are "zeroed", may well result in a fit
about as good as that using FOCE (in contrast to that shown
in Figure 3), and if the number of elements of
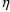 that are zeroed is large
relative to the total number of elements, CPU time may be
significantly reduced.
that are zeroed is large
relative to the total number of elements, CPU time may be
significantly reduced.
The ability of a conditional estimation method to
produce results different from those obtained with the FO
method decreases as the amount of data per individual
decreases. This is because the conditional methods use
conditional estimates of the
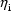 , which are all shrunken to
0, and the shrinkage is greater the less the amount of data
per individual. Actually, the amount of data from the ith
individual should be measured relative to the number of
parameters in the model for the individual, i.e. the number
of elements of
, which are all shrunken to
0, and the shrinkage is greater the less the amount of data
per individual. Actually, the amount of data from the ith
individual should be measured relative to the number of
parameters in the model for the individual, i.e. the number
of elements of 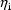 upon which
the model really depends. As the number of parameters
increases, the amount of data decreases, and can
"approach 0". Also, strictly speaking, the amount
of data might be understood as being relative to the
"data design" (the poorer the design, the less
useful the data) and the magnitude of intraindividual error
(the more error, the less useful the data).
upon which
the model really depends. As the number of parameters
increases, the amount of data decreases, and can
"approach 0". Also, strictly speaking, the amount
of data might be understood as being relative to the
"data design" (the poorer the design, the less
useful the data) and the magnitude of intraindividual error
(the more error, the less useful the data).
With intraindividual mean-variance models where
it may appear theoretically plausible that there is an
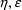 -interaction, it might seem
more appropriate to use the FOCE method with interaction
than to use the FOCE method without interaction. However,
when the amount of (true) intraindividual variance is large
(though the intraindividual models may be structurally
well-specified), or the amount of data per individual is
small, it will be difficult for the data to support an
-interaction, it might seem
more appropriate to use the FOCE method with interaction
than to use the FOCE method without interaction. However,
when the amount of (true) intraindividual variance is large
(though the intraindividual models may be structurally
well-specified), or the amount of data per individual is
small, it will be difficult for the data to support an
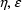 interaction, in which case
the FOCE method with interaction may produce no improvement
over the FOCE method without interaction. Otherwise, and
especially when intraindividual variance is small for some
observations, but not for others due to structural model
misspecification, and when there is considerable
interindividual variability, the FOCE method with no
interaction can lead to a noticeably biased fit (as can the
FO method).
interaction, in which case
the FOCE method with interaction may produce no improvement
over the FOCE method without interaction. Otherwise, and
especially when intraindividual variance is small for some
observations, but not for others due to structural model
misspecification, and when there is considerable
interindividual variability, the FOCE method with no
interaction can lead to a noticeably biased fit (as can the
FO method).
There seems to be no consistent relationship
between the value of the objective function using one method
and the value of the objective function using another
method. Therefore, objective function values should not be
compared across methods. However, objective function values
(in conjunction with graphical output) can provide a very
useful way to compare alternative models, as long as the
values are obtained using the same method.
III.B. Model Form
Unless interindividual variability is small, use
of a random interindividual effect in the model should be
such that quantities that depend on the effect are always
computed with physically meaningful values. For example,
rather than model a clearance parameter by
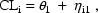
it is better to use
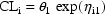
since clearance should always be positive. With
the FO method, use of either model produces essentially the
same results. (The formulas for clearance and for the
derivatives of clearance with respect to
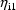 are computed only with the
value
are computed only with the
value 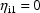 .) However, with a
conditional estimation method, different values of
.) However, with a
conditional estimation method, different values of
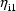 are tried. A negative value
for
are tried. A negative value
for 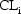 can result with the
first model, especially when
can result with the
first model, especially when
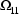 is large and large negative
values of
is large and large negative
values of 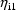 are
tried.
are
tried.
To take another example: Suppose that with the
one compartment linear model with first-order absorption
from a drug depot, it is assumed that pharmacokinetically,
for all individuals, the rate constant of absorption exceeds
the rate constant of elimination, i.e.
 . Instead of
. Instead of
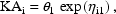
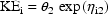
one should use
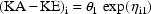
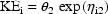
and constrain both
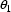 and
and
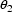 to be positive.
to be positive.
Again, with the FO method, use of either model produces
essentially the same
results.
The problem with the first model is that when using a
conditional estimation
method, as 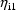 and
and
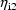 vary,
vary,
the value of 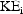 can exceed
can exceed
 ,
,
due to "flip-flop".
As this can happen, or not, from one individual to the next,
if it
happens at all, the conditional estimation method will
"become confused"
and fail. The conditional estimation method by itself has no
way of knowing
that it has been assumed that
 will not exceed
will not exceed
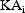 , and it
, and it
cannot distinguish flip-flop from this possibility. (If
pharmacokinetically,
occurs, again the conditional estimation method will become
confused, not
being able to distinguish flip-flop from these
possibilities, but in this case,
a modification of the model will not help.)
Consider again the simple model for a clearance
parameter,
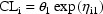
With the FO method, all derivatives with respect
to 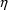 are evaluated at 0.
Consequently, in effect, a transformed model for
are evaluated at 0.
Consequently, in effect, a transformed model for
 is used: a first-order
approximation in
is used: a first-order
approximation in 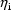 , of the
right side of the equation,
, of the
right side of the equation,

This is a constant cv type model. With the FO
method, no matter whether the given model or the transformed
model is "used", the results of the analysis will
be the same. The same is true even if covariates are
involved. However, when a population conditional estimation
method is used, the results of the analysis will differ
between the two models, as derivatives with respect to
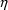 are evaluated at
conditional estimates.
are evaluated at
conditional estimates.
III.C. Role of the FO Method
The following general guidelines are offered so
that conditional estimation methods are used only when
necessary, and thus unnecessary expenditure of computer time
and other difficulties that sometimes arise with conditional
estimation methods (see section D) are avoided. They are
based on impressions, rather than systematic study. Clearly,
there will arise situations where alternative approaches
might be tried.
If the model is of a very nonlinear kind (see
section A), then from the outset, a conditional method might
be used instead of the FO method. Indeed, with models for
categorical- and discrete-ordinal type observations, the
Laplacian method should always be used, and the remainder of
this discussion concerns the use of conditional estimation
methods with models for continuous outcomes (more precisely,
the intraindividual models are of mean-variance
type).
When analyzing a new data set and/or using a very
new model with the data set, it is a good practice to use
the FO method with at least the first one or two NONMEM
runs, in order to simply check the data set and control
stream. The Estimation Steps with these runs should
terminate successfully, although if a conditional estimation
method is really needed, the results themselves may not be
entirely satisfactory. At this very early stage of data
analysis, the user needs to be able to detect elementary
errors that may have been introduced into the data set or
control stream, and to be able to detect significant
modeling difficulties. This cannot be done easily if other
unrelated problems that can arise with conditional
estimation methods interfere.
One might do well to begin to develop a complete
model, incorporating the covariates, etc., using the FO
method. Decisions regarding the effects of covariates on
randomly dispersed parameters are aided by examining
scatterplots of conditional estimates versus particular
covariates. When the FO method is used, the posthoc
estimates are the conditional estimates that are used for
this purpose. After it appears that the model can be
developed no further, there nonetheless exists appreciable
bias in the final fit, think about how this bias might be
well-explained by model misspecification that has not been
possible to address (e.g. there is a known covariate effect,
and the covariate has not been measured). The use of an
estimation method cannot really compensate for bias due to
model misspecification, and one should not imagine that a
conditional estimation method is any different.
After model development is complete using the FO
method, if there seems to be no bias in the fit, you might
simply want to do one run with FOCE to check this
impression. If after this, the fit does not significantly
improve, you can stop. After model development is complete
using the FO method, if there seems to be no bias in the
fit, consider doing one run with FOCE to obtain the best
possible estimates of variance-covariance components. The
variance-covariance components are often estimated better
using FOCE (but realize that sometimes, they may be
estimated very similarly by FO - see discussion in section
A), and when these estimates are important to you, it can
therefore be worthwhile investing the time needed with the
additional FOCE run. It is not necessary to use FOCE to
sharpen the estimates of variance-covariance components
until after an adequate model is developed using the FO
method.
After model development is complete using the FO
method, if appreciable unexplainable bias remains, do try
using FOCE. Indeed, do not hesitate to try FOCE before model
development is complete when a number of initial
concientious attempts to improve your model using FO have
resulted in considerable bias, and when conditions
are such that a priori, the FO and FOCE results are
not expected to be very similar (see background section).
When the intraindividual models you are using permit the
possibility of an 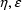 -interaction that the data may be rich enough to support,
try FOCE with interaction. If the use of FOCE significantly
reduces the bias, continue to develop the model using FOCE.
Or, before embarking on continued model development, first
experiment with the hybrid method to see whether this
produces as much bias reduction as does FOCE, along with
significant improvement in run time over FOCE. Continued
model development may entail repeating much of the work
already done with the FO method. In particular, try adding
covariates rejected when using the FO method, and reconsider
alternative ways that the covariates already accepted can
enter the model. As a result of the cost involved in
possibly needing to repeat work already undertaken with the
FO method, the question of how soon one begins to try FOCE
is not clearly answerable. Surely, increased computational
times must be considered, and usually one wants to delay
using a conditional estimation method until use of such a
method seems to be clearly indicated.
-interaction that the data may be rich enough to support,
try FOCE with interaction. If the use of FOCE significantly
reduces the bias, continue to develop the model using FOCE.
Or, before embarking on continued model development, first
experiment with the hybrid method to see whether this
produces as much bias reduction as does FOCE, along with
significant improvement in run time over FOCE. Continued
model development may entail repeating much of the work
already done with the FO method. In particular, try adding
covariates rejected when using the FO method, and reconsider
alternative ways that the covariates already accepted can
enter the model. As a result of the cost involved in
possibly needing to repeat work already undertaken with the
FO method, the question of how soon one begins to try FOCE
is not clearly answerable. Surely, increased computational
times must be considered, and usually one wants to delay
using a conditional estimation method until use of such a
method seems to be clearly indicated.
The model might be very nonlinear, in which case
try the Laplacian method. If after using the FOCE and
Laplacian conditional estimation methods, an appropriate
goodness-of-fit plot is unsatisfactory, then there is very
likely a modeling difficulty, and one must seriously
acknowledge this.
III.D. Role of Centering Methods
If after concientious modeling using the
appropriate (noncentering) conditional estimation method(s),
a model results with which substantial bias still appears in
the fit, there is probably a model-related explanation for
this, though it may allude one. In these circumstances, one
may want to proceed to obtain the best possible fit with the
model in hand. The fit that has been obtained using the
noncentering conditional estimation method is not
necessarily the best fit that may be obtained with the
misspecified model.
The bias may be reflected by an uncentered fit.
When a population conditional estimation method is used, the
average conditional estimate for each element of
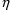 is given in NONMEM output
(the conditional estimates being averaged are those produced
by the method), along with a P-value that can be used to
help assess whether this average is sufficiently close to 0
(the null hypothesis). The occurence of at least one small
P-value (less than 0.05, though when the P-value is small,
it can be much less than 0.05) indicates an uncentered
fit.
is given in NONMEM output
(the conditional estimates being averaged are those produced
by the method), along with a P-value that can be used to
help assess whether this average is sufficiently close to 0
(the null hypothesis). The occurence of at least one small
P-value (less than 0.05, though when the P-value is small,
it can be much less than 0.05) indicates an uncentered
fit.
A centering method might be tried. Using
centering FOCE or centering Laplacian, one should notice
that the P-values are somewhat larger (although perhaps some
are still less than 0.05), and often one will also notice
considerable improvement in the fit to the data themselves.
When it is necessary to use a centering method, the
population parameter estimates (at least those identified
with the misspecified part of the model) are themselves of
little interest; population predictions under the fitted
model are what is of interest. Also, because the model is
misspecified, one should anticipate possible problems with
model validation and model applications involving
extrapolation.
Although it may be that (at least in certain
specifiable situations) fits with centering methods are in
general no worse than those obtained with appropriate
noncentering methods, this idea is not yet well enough
tested. Moreover, routine use of centering methods will mask
modeling problems. Centering methods should be used only
when, after concientious modeling, bias in fit seems
unavoidable. CENTERING METHODS SHOULD NOT BE ROUTINELY USED.
When the model is well-specified, it seems unlikely that
when using an appropriate noncentering method, bias in fit
will result, and there should be no expectation that any
further improvement can be gained with a centering
method.
Even when the fit is centered, it may be possible
(though rare) that the fit to the data themselves still
shows bias (see remarks in chapter II). One might then also
use centering FOCE with the first-order model, subject to
the same cautions given above. (Recall that in this case,
the conditional estimates of the
 resulting from the
centering method are based on linear intraindividual models.
When centering is actually needed, these conditional
estimates should probably be adequate for whatever purposes
conditional estimates might be used. It is possible
nonetheless to obtain posthoc estimates based on the given
intraindividual models.)
resulting from the
centering method are based on linear intraindividual models.
When centering is actually needed, these conditional
estimates should probably be adequate for whatever purposes
conditional estimates might be used. It is possible
nonetheless to obtain posthoc estimates based on the given
intraindividual models.)
Even when a model is well-specified, it may be so
complicated (e.g. it uses difficult differential equations)
that to use it with a conditional estimation method requires
a great amount of computer time. In this case, if indeed a
conditional estimation method is needed, one might use
centering FOCE with the first-order model, even though
centering per se may not be needed. In this situation, use
of centering, along with the first-order model, is just a
device allowing a conditional estimation method to be
implemented with less of a computational burden. A
compromise is achieved; the fit should appear to be an
improvement over that obtained with the FO fit, but it may
not be quite as good as one obtained with the noncentering
FOCE or Laplacian methods. Because the first-order model is
automatically obtained from the given model, the final form
of the given model (obtained after completing model
development) is readily available, and with this model, one
might try to implement one run using either the noncentering
FOCE or Laplacian methods and compare results.
III.E. Role of the Hybrid Method
As already noted in section A, use of the hybrid
method may require appreciably less computer time than the
FOCE method and yet result in as good a fit. There is
another important use of this method.
A change-point parameter of the ith
intraindividual model is a parameter of the model such that
for any value of 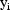 , the
derivative of
, the
derivative of 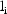 with respect
to this parameter, evaluated at some value of the parameter
(a change-point value , is undefined. An example of
this is an absorption lagtime parameter A of a
pharmacokinetic model for blood concentrations
with respect
to this parameter, evaluated at some value of the parameter
(a change-point value , is undefined. An example of
this is an absorption lagtime parameter A of a
pharmacokinetic model for blood concentrations
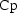 . If a dose is given at
time 0, then the derivative of the pharmacokinetic
expression for
. If a dose is given at
time 0, then the derivative of the pharmacokinetic
expression for  at time
at time
 with respect to A,
evaluated at
with respect to A,
evaluated at 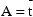 is undefined.
So if moreover, an observation
is undefined.
So if moreover, an observation
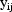 occurs at time
occurs at time
 (so that the expression for
(so that the expression for
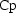 must be evaluated at this
time), then the derivative of
must be evaluated at this
time), then the derivative of
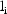 evaluated at
evaluated at
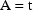 is undefined (for any value
of
is undefined (for any value
of 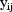 or for any of the other
observations of
or for any of the other
observations of 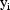 ).
Therefore under these circumstances, if the change-point
parameter is randomly dispersed, and
).
Therefore under these circumstances, if the change-point
parameter is randomly dispersed, and
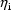 may assume a value at which
may assume a value at which
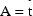 , then
, then
 is undefined at this value,
and, strictly speaking, all estimation methods described in
chapter II are undefined. But practically speaking, a method
will fail only when, during the search to minimize
is undefined at this value,
and, strictly speaking, all estimation methods described in
chapter II are undefined. But practically speaking, a method
will fail only when, during the search to minimize
 , a value of
, a value of
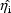 at which
at which
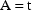 cannot be avoided. A
symptom that this is happening, when there is a randomly
dispersed change-point parameter, is a search terminization
with a large gradient, i.e. some gradient elements are
cannot be avoided. A
symptom that this is happening, when there is a randomly
dispersed change-point parameter, is a search terminization
with a large gradient, i.e. some gradient elements are
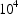 or larger. Often, a lagtime
is estimated to be very near the time of the first
observation within an individual record, and so the problem
described here can be a very real problem. One remedy is to
delete observations at times that are too close to estimated
lag times. However, aside from entailing the deletion of
legitimate data, there can also be implementation problems
with this strategy.
or larger. Often, a lagtime
is estimated to be very near the time of the first
observation within an individual record, and so the problem
described here can be a very real problem. One remedy is to
delete observations at times that are too close to estimated
lag times. However, aside from entailing the deletion of
legitimate data, there can also be implementation problems
with this strategy.
If the hybrid method is used, and the element(s)
of 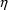 associated with the
change-point parameter - denote this by
associated with the
change-point parameter - denote this by
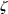 - is zeroed, this reduces
the number (across individuals) of values
- is zeroed, this reduces
the number (across individuals) of values
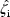 at which
at which
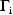 could possibly be undefined
in the computation, as only the value of the change-point
parameter for the typical subject is needed in the
computation. Indeed, unless the change-point parameter
itself depends on a covariate, only at the value
could possibly be undefined
in the computation, as only the value of the change-point
parameter for the typical subject is needed in the
computation. Indeed, unless the change-point parameter
itself depends on a covariate, only at the value
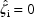 can
can
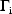 possibly be undefined in
the computation. Thus, the chance of the problem occurring
is reduced (but not eliminated).†
possibly be undefined in
the computation. Thus, the chance of the problem occurring
is reduced (but not eliminated).†
----------

III.F. Problems
A conditional estimation method can demonstrate
somewhat more sensitivity to rounding error problems during
the Estmation Step than will the FO method. When the search
for parameter estimates terminates with rounding error
problems, oftentimes intermediate output from the Estimation
Step will indicate the accuracy with which each of the final
parameter estimates has been obtained. For example, 3
significant digits may be requested for each estimate, but
for some estimates, less than 3 digits is actually obtained.
If only a little less than 3 digits is obtained (e.g.
2.7-2.9), and if the gradient vector of the objective
function with the final parameter estimates is small (e.g.
no element is greater than 5 in absolute value), then this
degree of accuracy is probably acceptable. If much less
accuracy is obtained, but only with those estimates where
this might be expected and where this is tolerable (e.g.
estimates of  elements),
then again, one might regard the Estimation Step as having
terminated successfully. (The order of the parameter
estimates printed in the iteration summaries is: the
elements),
then again, one might regard the Estimation Step as having
terminated successfully. (The order of the parameter
estimates printed in the iteration summaries is: the
 ’s in their
subscripted order, followed by the (unconstrained)
’s in their
subscripted order, followed by the (unconstrained)
 elements, followed by the
(unconstrained)
elements, followed by the
(unconstrained)  elements.
Note though, that these estimates are those of the scaled
transformed parameters (STP), rather than the original
parameters; see NONMEM Users Guide - Part I, section
C.3.5.1.)
elements.
Note though, that these estimates are those of the scaled
transformed parameters (STP), rather than the original
parameters; see NONMEM Users Guide - Part I, section
C.3.5.1.)
With a conditional estimation method (in contrast
with the FO method), NONMEM can more readily terminate
during the Estimation Step with a PRED error message
indicating e.g. that a nonallowable value for a parameter
has been computed in PRED code, perhaps a negative value for
a rate constant.†† This is because a parameter
may be randomly dispersed, and with a conditional estimation
method, values of 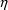 different
from 0 are tried, as well as are different values of
different
from 0 are tried, as well as are different values of
 , and some of these values
might result in a nonallowable value of the parameter. If
such a termination occurs, then, if not already doing so,
consider modeling the parameter in a way that prevents it
from assuming a nonallowable value, e.g if the parameter
cannot be negative, consider using a model such as
, and some of these values
might result in a nonallowable value of the parameter. If
such a termination occurs, then, if not already doing so,
consider modeling the parameter in a way that prevents it
from assuming a nonallowable value, e.g if the parameter
cannot be negative, consider using a model such as
 (see section B). Sometimes
this cannot completely solve the problem, e.g. if the
parameter cannot also be 0, the model just given will not
insure this (
(see section B). Sometimes
this cannot completely solve the problem, e.g. if the
parameter cannot also be 0, the model just given will not
insure this ( 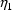 can be very
large and negative). So, a termination may still occur. The
next step is to try to include the NOABORT option
on the $ESTIMATION record (see NONMEM Users Guide - Part IV,
section IV.G.2). However, doing so will have no effect if
the termination occurs during the 0th
iteration.††† The NOABORT
option activates one type of PRED error-recovery
(THETA-recovery), and the other type (ETA-recovery) is
always activated, without using the option. So the option
may not need to be used initially, and if PREDPP is being
used, to have used the option before a termination has
actually occured has the detrimental effect that this can
mask the occurrence of an error detected by PREDPP, of which
the user needs to be informed. With PREDPP, never use
the NOABORT option until you have had an
opportunity (i) to see what happens when you do not use it,
i.e. to see the contents of PRED error messages that might
arise when you do not use the option, (ii) to respond, if
possible, to these messages in a sensible way (other than
using the option), and (iii) to see what happens after you
have done this.
can be very
large and negative). So, a termination may still occur. The
next step is to try to include the NOABORT option
on the $ESTIMATION record (see NONMEM Users Guide - Part IV,
section IV.G.2). However, doing so will have no effect if
the termination occurs during the 0th
iteration.††† The NOABORT
option activates one type of PRED error-recovery
(THETA-recovery), and the other type (ETA-recovery) is
always activated, without using the option. So the option
may not need to be used initially, and if PREDPP is being
used, to have used the option before a termination has
actually occured has the detrimental effect that this can
mask the occurrence of an error detected by PREDPP, of which
the user needs to be informed. With PREDPP, never use
the NOABORT option until you have had an
opportunity (i) to see what happens when you do not use it,
i.e. to see the contents of PRED error messages that might
arise when you do not use the option, (ii) to respond, if
possible, to these messages in a sensible way (other than
using the option), and (iii) to see what happens after you
have done this.
----------

Perhaps the operating system, rather than NONMEM,
terminates the program with a message indicating the
occurrence of a floating point exception in a user-code.
Again, this may be because a value
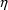 is tried which results in
the exception when a value of a randomly dispersed parameter
is computed. Underflows are ignorable, and terminations due
to underflows should be disabled (see NONMEM Users Guide -
Part III). With an operand error, or overflow, or
zero-divide, the user needs to identify where the exception
occurs in the code. For this purpose, the use of a debugger,
or debugging print statements in the code, may be helpful.
Then perhaps the exception may be avoided by using PRED
error-recovery in the user-code, i.e. by using the EXIT
statement with return code 1 (see NONMEM Users Guide - Part
IV, section IV.G.2). Try this, and rerun. If with the
earlier run, the termination occured after the 0th
iteration, and if PREDPP is not being used, rerun the
problem using the NOABORT option on the $ESTIMATION
record. If the termination occured after the 0th iteration,
and if PREDPP is being used, rerun, but do not use
the NOABORT option. If the termination
still occurs, then rerun a second time, this time using the
NOABORT option. If the termination occurs during
the 0th iteration, the NOABORT option has no
effect. Such a termination can arise due to a problem with
either the data set, user code, or control stream. Different
initial estimates might be tried (perhaps smaller
interindividual variances).
is tried which results in
the exception when a value of a randomly dispersed parameter
is computed. Underflows are ignorable, and terminations due
to underflows should be disabled (see NONMEM Users Guide -
Part III). With an operand error, or overflow, or
zero-divide, the user needs to identify where the exception
occurs in the code. For this purpose, the use of a debugger,
or debugging print statements in the code, may be helpful.
Then perhaps the exception may be avoided by using PRED
error-recovery in the user-code, i.e. by using the EXIT
statement with return code 1 (see NONMEM Users Guide - Part
IV, section IV.G.2). Try this, and rerun. If with the
earlier run, the termination occured after the 0th
iteration, and if PREDPP is not being used, rerun the
problem using the NOABORT option on the $ESTIMATION
record. If the termination occured after the 0th iteration,
and if PREDPP is being used, rerun, but do not use
the NOABORT option. If the termination
still occurs, then rerun a second time, this time using the
NOABORT option. If the termination occurs during
the 0th iteration, the NOABORT option has no
effect. Such a termination can arise due to a problem with
either the data set, user code, or control stream. Different
initial estimates might be tried (perhaps smaller
interindividual variances).
TOP
TABLE OF CONTENTS
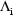 are
evaluated at the conditional estimates, rather than at 0).
Similarly, the hybrid method should also perform no worse
than the FO method, but perhaps not as well as the FOCE
method. (See e.g. Figure 3, which is the goodness-of-fit
plot for the same data described above, using the hybrid
method (with two out of four
are
evaluated at the conditional estimates, rather than at 0).
Similarly, the hybrid method should also perform no worse
than the FO method, but perhaps not as well as the FOCE
method. (See e.g. Figure 3, which is the goodness-of-fit
plot for the same data described above, using the hybrid
method (with two out of four 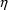 ’s "zeroed".)) This defines a type of
hierarchy to the methods.
’s "zeroed".)) This defines a type of
hierarchy to the methods. increases. The need to use the Laplacian method increases
because as the degree of nonlinearity increases, the
adequacy of the first-order approximation decreases. The
need to use the FOCE method increases because as the degree
of nonlinearity increases, the adequacy of the first-order
approximation depends more on the values at which the
increases. The need to use the Laplacian method increases
because as the degree of nonlinearity increases, the
adequacy of the first-order approximation decreases. The
need to use the FOCE method increases because as the degree
of nonlinearity increases, the adequacy of the first-order
approximation depends more on the values at which the
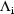 are evaluated.
are evaluated. decreases. This is because
the conditional methods use conditional estimates of the
decreases. This is because
the conditional methods use conditional estimates of the
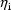 , which are all shrunken to
0, and the shrinkage is greater the smaller the size of
, which are all shrunken to
0, and the shrinkage is greater the smaller the size of
 . The value 0 is the value
used for the
. The value 0 is the value
used for the 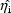 with the FO
method. Similarly, the ability of FOCE to produce results
different from those obtained with the hybrid method
decreases as the degree of random interindividual
variablity, i.e. "the size" of
with the FO
method. Similarly, the ability of FOCE to produce results
different from those obtained with the hybrid method
decreases as the degree of random interindividual
variablity, i.e. "the size" of
 decreases. In fact, suppose
one tries to use the FOCE method and finds that some
estimates of interindividual variances are rather large
compared to others. Then using the hybrid method where those
elements of
decreases. In fact, suppose
one tries to use the FOCE method and finds that some
estimates of interindividual variances are rather large
compared to others. Then using the hybrid method where those
elements of 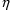 with small
variance are "zeroed", may well result in a fit
about as good as that using FOCE (in contrast to that shown
in Figure 3), and if the number of elements of
with small
variance are "zeroed", may well result in a fit
about as good as that using FOCE (in contrast to that shown
in Figure 3), and if the number of elements of
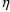 that are zeroed is large
relative to the total number of elements, CPU time may be
significantly reduced.
that are zeroed is large
relative to the total number of elements, CPU time may be
significantly reduced.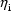 , which are all shrunken to
0, and the shrinkage is greater the less the amount of data
per individual. Actually, the amount of data from the ith
individual should be measured relative to the number of
parameters in the model for the individual, i.e. the number
of elements of
, which are all shrunken to
0, and the shrinkage is greater the less the amount of data
per individual. Actually, the amount of data from the ith
individual should be measured relative to the number of
parameters in the model for the individual, i.e. the number
of elements of 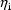 upon which
the model really depends. As the number of parameters
increases, the amount of data decreases, and can
"approach 0". Also, strictly speaking, the amount
of data might be understood as being relative to the
"data design" (the poorer the design, the less
useful the data) and the magnitude of intraindividual error
(the more error, the less useful the data).
upon which
the model really depends. As the number of parameters
increases, the amount of data decreases, and can
"approach 0". Also, strictly speaking, the amount
of data might be understood as being relative to the
"data design" (the poorer the design, the less
useful the data) and the magnitude of intraindividual error
(the more error, the less useful the data).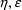 -interaction, it might seem
more appropriate to use the FOCE method with interaction
than to use the FOCE method without interaction. However,
when the amount of (true) intraindividual variance is large
(though the intraindividual models may be structurally
well-specified), or the amount of data per individual is
small, it will be difficult for the data to support an
-interaction, it might seem
more appropriate to use the FOCE method with interaction
than to use the FOCE method without interaction. However,
when the amount of (true) intraindividual variance is large
(though the intraindividual models may be structurally
well-specified), or the amount of data per individual is
small, it will be difficult for the data to support an
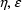 interaction, in which case
the FOCE method with interaction may produce no improvement
over the FOCE method without interaction. Otherwise, and
especially when intraindividual variance is small for some
observations, but not for others due to structural model
misspecification, and when there is considerable
interindividual variability, the FOCE method with no
interaction can lead to a noticeably biased fit (as can the
FO method).
interaction, in which case
the FOCE method with interaction may produce no improvement
over the FOCE method without interaction. Otherwise, and
especially when intraindividual variance is small for some
observations, but not for others due to structural model
misspecification, and when there is considerable
interindividual variability, the FOCE method with no
interaction can lead to a noticeably biased fit (as can the
FO method).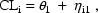
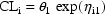
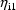 are computed only with the
value
are computed only with the
value 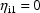 .) However, with a
conditional estimation method, different values of
.) However, with a
conditional estimation method, different values of
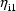 are tried. A negative value
for
are tried. A negative value
for  can result with the
first model, especially when
can result with the
first model, especially when
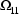 is large and large negative
values of
is large and large negative
values of 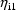 are
tried.
are
tried. . Instead of
. Instead of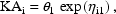
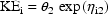
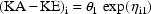
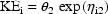
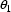 and
and
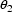 to be positive.
to be positive.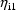 and
and
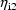 vary,
vary,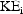 can exceed
can exceed
 ,
, will not exceed
will not exceed
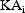 , and it
, and it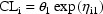
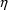 are evaluated at 0.
Consequently, in effect, a transformed model for
are evaluated at 0.
Consequently, in effect, a transformed model for
 is used: a first-order
approximation in
is used: a first-order
approximation in 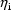 , of the
right side of the equation,
, of the
right side of the equation,
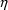 are evaluated at
conditional estimates.
are evaluated at
conditional estimates.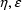 -interaction that the data may be rich enough to support,
try FOCE with interaction. If the use of FOCE significantly
reduces the bias, continue to develop the model using FOCE.
Or, before embarking on continued model development, first
experiment with the hybrid method to see whether this
produces as much bias reduction as does FOCE, along with
significant improvement in run time over FOCE. Continued
model development may entail repeating much of the work
already done with the FO method. In particular, try adding
covariates rejected when using the FO method, and reconsider
alternative ways that the covariates already accepted can
enter the model. As a result of the cost involved in
possibly needing to repeat work already undertaken with the
FO method, the question of how soon one begins to try FOCE
is not clearly answerable. Surely, increased computational
times must be considered, and usually one wants to delay
using a conditional estimation method until use of such a
method seems to be clearly indicated.
-interaction that the data may be rich enough to support,
try FOCE with interaction. If the use of FOCE significantly
reduces the bias, continue to develop the model using FOCE.
Or, before embarking on continued model development, first
experiment with the hybrid method to see whether this
produces as much bias reduction as does FOCE, along with
significant improvement in run time over FOCE. Continued
model development may entail repeating much of the work
already done with the FO method. In particular, try adding
covariates rejected when using the FO method, and reconsider
alternative ways that the covariates already accepted can
enter the model. As a result of the cost involved in
possibly needing to repeat work already undertaken with the
FO method, the question of how soon one begins to try FOCE
is not clearly answerable. Surely, increased computational
times must be considered, and usually one wants to delay
using a conditional estimation method until use of such a
method seems to be clearly indicated.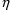 is given in NONMEM output
(the conditional estimates being averaged are those produced
by the method), along with a P-value that can be used to
help assess whether this average is sufficiently close to 0
(the null hypothesis). The occurence of at least one small
P-value (less than 0.05, though when the P-value is small,
it can be much less than 0.05) indicates an uncentered
fit.
is given in NONMEM output
(the conditional estimates being averaged are those produced
by the method), along with a P-value that can be used to
help assess whether this average is sufficiently close to 0
(the null hypothesis). The occurence of at least one small
P-value (less than 0.05, though when the P-value is small,
it can be much less than 0.05) indicates an uncentered
fit. resulting from the
centering method are based on linear intraindividual models.
When centering is actually needed, these conditional
estimates should probably be adequate for whatever purposes
conditional estimates might be used. It is possible
nonetheless to obtain posthoc estimates based on the given
intraindividual models.)
resulting from the
centering method are based on linear intraindividual models.
When centering is actually needed, these conditional
estimates should probably be adequate for whatever purposes
conditional estimates might be used. It is possible
nonetheless to obtain posthoc estimates based on the given
intraindividual models.)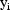 , the
derivative of
, the
derivative of 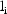 with respect
to this parameter, evaluated at some value of the parameter
(a change-point value , is undefined. An example of
this is an absorption lagtime parameter A of a
pharmacokinetic model for blood concentrations
with respect
to this parameter, evaluated at some value of the parameter
(a change-point value , is undefined. An example of
this is an absorption lagtime parameter A of a
pharmacokinetic model for blood concentrations
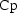 . If a dose is given at
time 0, then the derivative of the pharmacokinetic
expression for
. If a dose is given at
time 0, then the derivative of the pharmacokinetic
expression for  at time
at time
 with respect to A,
evaluated at
with respect to A,
evaluated at 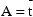 is undefined.
So if moreover, an observation
is undefined.
So if moreover, an observation
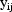 occurs at time
occurs at time
 (so that the expression for
(so that the expression for
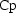 must be evaluated at this
time), then the derivative of
must be evaluated at this
time), then the derivative of
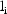 evaluated at
evaluated at
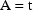 is undefined (for any value
of
is undefined (for any value
of 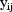 or for any of the other
observations of
or for any of the other
observations of 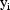 ).
Therefore under these circumstances, if the change-point
parameter is randomly dispersed, and
).
Therefore under these circumstances, if the change-point
parameter is randomly dispersed, and
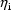 may assume a value at which
may assume a value at which
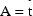 , then
, then
 is undefined at this value,
and, strictly speaking, all estimation methods described in
chapter II are undefined. But practically speaking, a method
will fail only when, during the search to minimize
is undefined at this value,
and, strictly speaking, all estimation methods described in
chapter II are undefined. But practically speaking, a method
will fail only when, during the search to minimize
 , a value of
, a value of
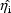 at which
at which
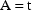 cannot be avoided. A
symptom that this is happening, when there is a randomly
dispersed change-point parameter, is a search terminization
with a large gradient, i.e. some gradient elements are
cannot be avoided. A
symptom that this is happening, when there is a randomly
dispersed change-point parameter, is a search terminization
with a large gradient, i.e. some gradient elements are
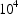 or larger. Often, a lagtime
is estimated to be very near the time of the first
observation within an individual record, and so the problem
described here can be a very real problem. One remedy is to
delete observations at times that are too close to estimated
lag times. However, aside from entailing the deletion of
legitimate data, there can also be implementation problems
with this strategy.
or larger. Often, a lagtime
is estimated to be very near the time of the first
observation within an individual record, and so the problem
described here can be a very real problem. One remedy is to
delete observations at times that are too close to estimated
lag times. However, aside from entailing the deletion of
legitimate data, there can also be implementation problems
with this strategy.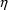 associated with the
change-point parameter - denote this by
associated with the
change-point parameter - denote this by
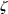 - is zeroed, this reduces
the number (across individuals) of values
- is zeroed, this reduces
the number (across individuals) of values
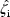 at which
at which
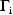 could possibly be undefined
in the computation, as only the value of the change-point
parameter for the typical subject is needed in the
computation. Indeed, unless the change-point parameter
itself depends on a covariate, only at the value
could possibly be undefined
in the computation, as only the value of the change-point
parameter for the typical subject is needed in the
computation. Indeed, unless the change-point parameter
itself depends on a covariate, only at the value
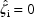 can
can
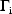 possibly be undefined in
the computation. Thus, the chance of the problem occurring
is reduced (but not eliminated).†
possibly be undefined in
the computation. Thus, the chance of the problem occurring
is reduced (but not eliminated).†
 elements),
then again, one might regard the Estimation Step as having
terminated successfully. (The order of the parameter
estimates printed in the iteration summaries is: the
elements),
then again, one might regard the Estimation Step as having
terminated successfully. (The order of the parameter
estimates printed in the iteration summaries is: the
 ’s in their
subscripted order, followed by the (unconstrained)
’s in their
subscripted order, followed by the (unconstrained)
 elements, followed by the
(unconstrained)
elements, followed by the
(unconstrained)  elements.
Note though, that these estimates are those of the scaled
transformed parameters (STP), rather than the original
parameters; see NONMEM Users Guide - Part I, section
C.3.5.1.)
elements.
Note though, that these estimates are those of the scaled
transformed parameters (STP), rather than the original
parameters; see NONMEM Users Guide - Part I, section
C.3.5.1.)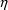 different
from 0 are tried, as well as are different values of
different
from 0 are tried, as well as are different values of
 , and some of these values
might result in a nonallowable value of the parameter. If
such a termination occurs, then, if not already doing so,
consider modeling the parameter in a way that prevents it
from assuming a nonallowable value, e.g if the parameter
cannot be negative, consider using a model such as
, and some of these values
might result in a nonallowable value of the parameter. If
such a termination occurs, then, if not already doing so,
consider modeling the parameter in a way that prevents it
from assuming a nonallowable value, e.g if the parameter
cannot be negative, consider using a model such as
 (see section B). Sometimes
this cannot completely solve the problem, e.g. if the
parameter cannot also be 0, the model just given will not
insure this (
(see section B). Sometimes
this cannot completely solve the problem, e.g. if the
parameter cannot also be 0, the model just given will not
insure this ( 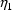 can be very
large and negative). So, a termination may still occur. The
next step is to try to include the NOABORT option
on the $ESTIMATION record (see NONMEM Users Guide - Part IV,
section IV.G.2). However, doing so will have no effect if
the termination occurs during the 0th
iteration.††† The NOABORT
option activates one type of PRED error-recovery
(THETA-recovery), and the other type (ETA-recovery) is
always activated, without using the option. So the option
may not need to be used initially, and if PREDPP is being
used, to have used the option before a termination has
actually occured has the detrimental effect that this can
mask the occurrence of an error detected by PREDPP, of which
the user needs to be informed. With PREDPP, never use
the NOABORT option until you have had an
opportunity (i) to see what happens when you do not use it,
i.e. to see the contents of PRED error messages that might
arise when you do not use the option, (ii) to respond, if
possible, to these messages in a sensible way (other than
using the option), and (iii) to see what happens after you
have done this.
can be very
large and negative). So, a termination may still occur. The
next step is to try to include the NOABORT option
on the $ESTIMATION record (see NONMEM Users Guide - Part IV,
section IV.G.2). However, doing so will have no effect if
the termination occurs during the 0th
iteration.††† The NOABORT
option activates one type of PRED error-recovery
(THETA-recovery), and the other type (ETA-recovery) is
always activated, without using the option. So the option
may not need to be used initially, and if PREDPP is being
used, to have used the option before a termination has
actually occured has the detrimental effect that this can
mask the occurrence of an error detected by PREDPP, of which
the user needs to be informed. With PREDPP, never use
the NOABORT option until you have had an
opportunity (i) to see what happens when you do not use it,
i.e. to see the contents of PRED error messages that might
arise when you do not use the option, (ii) to respond, if
possible, to these messages in a sensible way (other than
using the option), and (iii) to see what happens after you
have done this.
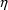 is tried which results in
the exception when a value of a randomly dispersed parameter
is computed. Underflows are ignorable, and terminations due
to underflows should be disabled (see NONMEM Users Guide -
Part III). With an operand error, or overflow, or
zero-divide, the user needs to identify where the exception
occurs in the code. For this purpose, the use of a debugger,
or debugging print statements in the code, may be helpful.
Then perhaps the exception may be avoided by using PRED
error-recovery in the user-code, i.e. by using the EXIT
statement with return code 1 (see NONMEM Users Guide - Part
IV, section IV.G.2). Try this, and rerun. If with the
earlier run, the termination occured after the 0th
iteration, and if PREDPP is not being used, rerun the
problem using the NOABORT option on the $ESTIMATION
record. If the termination occured after the 0th iteration,
and if PREDPP is being used, rerun, but do not use
the NOABORT option. If the termination
still occurs, then rerun a second time, this time using the
NOABORT option. If the termination occurs during
the 0th iteration, the NOABORT option has no
effect. Such a termination can arise due to a problem with
either the data set, user code, or control stream. Different
initial estimates might be tried (perhaps smaller
interindividual variances).
is tried which results in
the exception when a value of a randomly dispersed parameter
is computed. Underflows are ignorable, and terminations due
to underflows should be disabled (see NONMEM Users Guide -
Part III). With an operand error, or overflow, or
zero-divide, the user needs to identify where the exception
occurs in the code. For this purpose, the use of a debugger,
or debugging print statements in the code, may be helpful.
Then perhaps the exception may be avoided by using PRED
error-recovery in the user-code, i.e. by using the EXIT
statement with return code 1 (see NONMEM Users Guide - Part
IV, section IV.G.2). Try this, and rerun. If with the
earlier run, the termination occured after the 0th
iteration, and if PREDPP is not being used, rerun the
problem using the NOABORT option on the $ESTIMATION
record. If the termination occured after the 0th iteration,
and if PREDPP is being used, rerun, but do not use
the NOABORT option. If the termination
still occurs, then rerun a second time, this time using the
NOABORT option. If the termination occurs during
the 0th iteration, the NOABORT option has no
effect. Such a termination can arise due to a problem with
either the data set, user code, or control stream. Different
initial estimates might be tried (perhaps smaller
interindividual variances).