NONMEM Users Guide Part V - Introductory Guide - Chapter 13
Chapter 13 - Errors in NONMEM Runs
This chapter describes error messages that can appear in NONMEM’s output and discusses some possible causes and remedies. It is not encyclopedic; only selected messages are discussed. NM-TRAN messages are meant to be self-explanatory, as are many PREDPP messages, and important NONMEM messages are documented in NONMEM Users Guide, Part I, Chapter G. Unlike certain other regression programs, NONMEM-PREDPP will not try to mask what is perceived as a real problem and to which attention must be given by the user before the computation can proceed; an error message results and often, the program terminates.
The Estimation and Covariance Steps do not always terminate successfully. This is a normal part of the process of model building. Sections 2 and 3 contain a discussion of the kinds of errors that can be expected to arise. Section 4 contains a discussion of some miscellaneous problems which can arise. Section 5 contains a discussion of some errors which arise when using PREDPP in particular.
Normal termination of the Estimation Step is indicated by the message:
MINIMIZATION SUCCESSFUL
Even when this message is seen, it is possible
that the Estimation Step has not run correctly. Final
estimates should be different from initial estimates. If the
initial and final estimates are the same and the gradients
for a parameter are zero at every iteration†, this is
a sign of a modelling error. The parameter does not affect
any predictions, as discussed in Chapter 7, Section 4.2. If
there were bounds, estimates should be well away from the
bounds. A final estimate which is close to a bound is
discussed in Chapter 11, Section 4.3.
----------
Abnormal termination of the Estimation Step is indicated by a message whose first line is:
MINIMIZATION TERMINATED
One of several messages will follow, indicating the type of failure. The messages are listed in Users Guide I.
Two of the most common are discussed here separately.
If after any iteration the total number of evaluations of the objective function (Chapter 10, figure 10.5, line 33) is equal to or greater than the maximum allowed (Chapter 10, figure 10.2, line 51), the minimization search is halted with this message. If the $ESTIMATION record requested that a Model Specification File be written, it is possible to continue the search from this point in a subsequent NONMEM run. In Chapter 12, Section 4.3, a strategy is discussed by which the number of function evaluations is deliberately set to a low value in order to structure a lengthy run as a series of shorter runs.
Whenever this message is obtained, it is important to examine the intermediate output and evaluate the progress made so far. A poorly-specified model, for example, may cause very slow convergence of the minimization search. Raising the maximum number of function evaluations (using the MAXEVAL option of the $ESTIMATION record) may not be advisable.
This message will be accompanied in the intermediate output by a message beginning: NUMSIGDIG: .... which gives the approximate number of significant digits obtained in each of the parameters being estimated. At least one such number will be less than the number requested.
Two cases must be distinguished.
Sometimes the Estimation Step terminates with this message after only a few iterations. If the value of the objective function is reasonable, but the initial gradients are zero at the end of the 0th iteration, it may be that there is an error in setting a machine-dependent constant (see Section 4.1.1), or the user has mixed double precision NONMEM or PREDPP or PRED routines with single precision NONMEM or PREDPP or PRED routines (see Section 4.1.2).
The objective function and gradients start with reasonable values and then decrease. If the run was done using single precision arithmetic on a computer with a small (32 bit) word length, it might be tried again using double precision. Whatever precision is used, the number of significant digits obtained should be examined. If it is at least 2, and the gradient vector appears stable throughout the last few iterations, a satisfactory minimum may well have been obtained. (It may be desirable to re-run the problem with the print interval for iteration summarization set to 1 (PRINT=1 in the $ESTIMATION record) so that the progress made at every iteration can be examined.) The final parameter estimates should be examined, and if they appear reasonable, they might be accepted. Although the user may have requested more than 2 significant digits, the data may only support about 2 digits, given the precision of the arithmetic being used. By examining the gradients carefully, it is often possible to obtain further information about which parameter estimates are less-well determined.
Even though the final parameter estimates may be adequate, it is unlikely that the minimum is sufficiently well-determined to allow the Covariance Step to run successfully, at least with the number of significant figures requested in the Estimation Step. The Estimation Step may need to be rerun, requesting only 2 significant figures, followed by the Covariance Step.
If the number of significant digits is less than 2 (or even negative), then the final estimates should not be trusted. The problem may be model misspecification or insufficient data.
Model misspecification is a very general problem involving some mismatch between the model and the data. This can result in particularly large values of the objective function or slow convergence of the minimization search. Sometimes the model is overparameterized. This means that the model has more parameters than can be well-enough estimated from the data (e.g., a biexponential model is fit to monoexponential data). When model misspecification occurs due to over-parameterization, then the Estimation Step will usually proceed smoothly, but terminate with fewer than 2 significant digits. It is best to start with simple models (see Chapter 11).
A related problem arises when a covariance
element, e.g.,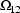 
(or
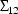), is being estimated. If
the ID (or L2 data item) is not used correctly, it may
appear as though the covariance does not affect objective
function values, and then this parameter will not be well
estimated. In other words, it may appear as though the model
is overparameterized due to the inclusion of this parameter.
See Chapter 12, Section 4.2.
It is possible for the Estimation Step to terminate successfully, and yet the Covariance Step generates an error message. Error messages from the Covariance Step are printed immediately after line 46 of Figure 10.5. The messages are listed in Users Guide I.
When a message arises, often it is:
R MATRIX ALGORITHMICALLY
NON-POSITIVE-SEMIDEFINITE
BUT NONSINGULAR
COVARIANCE STEP ABORTED
In order for the minimization routine to terminate successfully, it needs to determine that the final gradient vector is sufficiently small, which is a necessary condition for a minimum to have been achieved. This condition, however, is not sufficient. A sufficient condition, that the R matrix be positive definite (and therefore, that the apparent minimum not be a saddle point) is only checked in the Covariance Step. The message means that the sufficient condition appears not to be satisfied. The final estimate is, therefore, in doubt.
Sometimes the message is:
R MATRIX ALGORITHMICALLY SINGULAR
COVARIANCE STEP UNOBTAINABLE
S MATRIX ALGORITHMICALLY SINGULAR
This arises when there exists a parameter whose values do not actually affect the predictions and whose gradient in the intermediate output is always 0.
In general, successful completion of the Covariance Step requires a better defined minimum than does the successful completion of the Estimation Step.
This section first discusses a few simple errors which prevent NONMEM-PREDPP from running successfully. Then the subject of machine interrupts is discussed.
Although we assume in this Guide that NONMEM-PREDPP is already installed correctly, errors may be made in running the system that can cause serious numerical problems, preventing even the examples from the Users Guide from running correctly. NONMEM uses certain constants whose value must be tailored to the specific machine on which NONMEM is running. These machine-dependent constants are set in a subroutine called BLKDAT. The way this is done, and the values appropriate to various computer architectures, are documented in NONMEM Users Guide, Part III (NONMEM Installation Guide). NONMEM will fail if the BLKDAT routine is not included in the NONMEM load module. Even if it is included, NONMEM may not run properly if the wrong constants are used. One should not run one or two examples and assume that because these appear to give correct output, the constants are appropriately set. For the purpose of future work with the program, it is important to check carefully that the constants are set as described in the Installation Guide.
It is extremely important that all routines use the same precision. All gradients, or alternating gradients, may be zero at every iteration when routines of mixed precision are combined.
With double precision NONMEM, use double precision PREDPP. Make sure that any user-written subroutines also declare as double precision the THETA array and every intermediate quantity computed using its elements. With single precision NONMEM-PREDPP, be sure to include the option "SUBROUTINES=SINGLE" on the $SUBROUTINE record.
A common error is to use the proportional error model while some predicted values for actual observations are zero or close to zero. (For example, if the first dose is an infusion and there is a "baseline" observation at the start of the infusion, the predicted level will be zero.)
With individual data this will lead to an error message similar to the following (the individual number may be different from 1):
PROGRAM TERMINATED BY OBJ, ERROR IN ELS WITH INDIVIDUAL 1 (IN INDIVIDUAL RECORD ORDERING) VAR-COV OF DATA FROM INDIVIDUAL RECORD ESTIMATED TO BE SINGULAR
With population data this will lead to an error message similar to the following (the individual and record numbers may be different than 1):
PROGRAM TERMINATED BY OBJ, ERROR IN CELS WITH INDIVIDUAL 1 (IN INDIVIDUAL RECORD ORDERING) INTRAINDIVIDUAL VARIANCE OF DATA FROM OBS RECORD 1 ESTIMATED TO BE 0
When using a new model, a run should done in
which the Estimation Step is not run, and a scatterplot of
PRED vs DV with unit slope line is produced, to verify that
the model and the initial parameter estimates are
reasonable. It is much harder to diagnose errors in the
model or the initial estimates after the Estimation Step
fails. Make sure that the initial value of the objective
function is not excessively large, and that the unit slope
line shows on the plot: scaling errors can easily go
undetected! E.g., if the units are incorrect at some point
in the model (L vs ml), the predictions may be wrong by a
factor of 1000. Similarly, if no scale was specified for the
compartment being observed, the predictions for the
observations are compartment amounts rather than
concentrations. In both cases, the shape of the PRED vs DV
plot may appear linear, but the axes may be labeled quite
differently. When observations from two different
compartments are present in the data (e.g.,
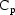and
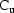), some of the observations
may be scaled incorrectly. This is discussed in Chapter 6,
Section 9, and Chapter 7, Section 4.3.3.
Some computers and operating systems are capable of detecting that an incorrect numerical operation has occurred, such as a division by zero, or a floating point underflow or overflow. On such a computer, a NONMEM run may terminate with an operating system error message indicating that a machine interrupt at the point of a numerical operation has occurred. Such an interrupt may indicate a problem regarding program installation or, perhaps, a bug in a program. In the latter case the bug could be in NONMEM or PREDPP, or it could be in the user’s abbreviated or user-written code. Most operating systems also can give some assistance by identifying the name of the subroutine in which the interrupt occurs, the line number in the source code, etc. Thus, the user can first check whether his own code may be causing the problem. With this information in hand, it may be helpful to ask the NONMEM consultant for assistance.
It is important to determine whether the interrupt occurs with the initial parameter estimates. It may help to run the problem without the Estimation Step, and with all initial estimates included in the control stream. Then either the objective function will be properly evaluated and output, or the interrupt will occur with the initial estimates.
If the interrupt occurs with the initial estimates, there is likely something wrong with the problem specification, and the NM-TRAN control stream and data file should be carefully checked. If the interrupt occurs during the first or later iterations of the minimization search, it may help to constrain the parameters to reasonable values (but see Chapter 11, Section 4.3). One way of constraining parameters is to explicitly test their values within user-written or abbreviated code, and to return an error return code to NONMEM when some parameter value is unreasonable. With abbreviated code, the EXIT statement can be used for this purpose. See Chapter 12, Section 4.15.
Some operating systems include a recovery procedure which allows a computation to proceed despite an interrupt. In the case of floating-point underflow, for example, such a procedure will generally set the result of the computation to zero and allow the program to continue. This particular recovery is ideal. If the operating system allows the user to choose whether or not to continue despite interrupts, it may be acceptable in some cases to instruct it to continue if the interrupt occurs during the Estimation Step. The search may proceed and move the parameter estimates away from the values that caused interrupts. This is discussed in Users Guide III, Chapter III, Section 2.9.
One should not, however, ignore the presence of interrupts merely because the results appear reasonable. It is better to revise the problem specification to avoid the interrupts.
TRANS routines can produce error messages. Here
is one from TRANS2:
ERROR IN TRANS2 ROUTINE: V IS ZERO
Appendix 2 shows that TRANS2 normally computes
K=CL/V. The routine checks that V is not zero, and
upon finding that it is, it prints the informative message,
and terminates the run (thus avoiding a machine
"division by zero" interrupt by the operating
system). This error usually occurs with the initial
parameter estimates. E.g., suppose the relevant $PK
statement is:
V=THETA(1)+WT*THETA(2)
For some values of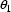 
,
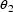, and WT, a value of zero is
being computed for V. The initial estimates of
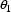and
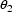should be checked. The
intercept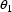 
might have been
fixed to zero, in which case then, the values of WT should
also be checked. If WT is recorded only on the first event
record of each individual’s data, careful coding is
required to insure that a value of zero is not used when the
$PK record is evaluated with subsequent event
records.
A similar error message can be generated in
PREDPP, e.g.
PK PARAMETER FOR OBSERVATION COMPARTMENT’S SCALE IS
ZERO
Some scale parameter is modeled in such a way as to produce
a zero. Again, the code for that scale parameter, and the
initial estimates for the 
’s used therein, should be checked. Perhaps the scale
parameter is being set equal to a volume parameter, and as
described above, the volume parameter is being set to zero.
When TRANS1 is used, the volume parameter is neither
recognized nor checked.
Floating point underflow machine interrupts can
occur with linear pharmacokinetic models (e.g., ADVAN1-4) in
the process of computing certain exponentials. They can
occur from an error in the units of either a rate constant
and/or the TIME data items. They can also occur from
inordinately large values for a rate constant which arise
during the minimization search. This might be avoided by
placing appropriate constraints on
’s.
Underflow interrupts can also occur when the system is advanced over an excessively long period of time. This can happen within an individual record, when the individual had a course of drug treatment, followed by a wash-out period, followed by another course of drug treatment. The first dose record of treatment courses other than the first should have EVID data item equal to 4 (reset-dose) rather than 1 (dose), to avoid computing excessively small compartment amounts (see Chapter 6, Section 7.3), and to reduce computational cost.
If the system recovery procedure sets the result of the computation to zero (see Users Guide III, Chapter III, Section 2.9), an underflow presents no particular problem.
Floating point overflow machine interrupts can
occur in the process of computing predictions with ADVAN2
and ADVAN4 when values of KA and K arise during the
minimization search that are very close to one another. The
models encoded into the ADVAN routines assume that KA and K
have fairly distinct values, and the formulas for the
predictions have the term KA-K in the denominator. If, for
example, the typical values of K and KA are associated with
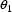and
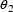, respectively, then one
might try reparameterizing. The typical values of K and KA-K
can be associated with 
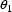and
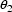, so that
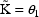and
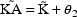. A lower bound of zero
should be placed on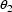 
†.
----------
A similar situation occurs with TRANS3, where
VSS-V occurs in the denominator of the expression for K21.
As above, reparameterization and a constraint on an element
of 
may help.