1. What This Chapter is About
2. General
3. Structural Parameter Models
3.1. Linear Models
3.2. Multiplicative Models
3.3. Saturation Models
3.4. Models with Indicator Variables
3.4.1. Combinations
3.4.2. Time Varying 
3.5. Structural Kinetic Models
4. Population Random Effects Models
4.1. Models for Interindividual Errors
4.1.1. Additive/Multiplicative Models
4.1.2. Other Models
4.1.3. General Form for the Parameter Model
4.2. Statistical Models for an Individual’s Observations
5. The Population Mixed Effects Model
NONMEM Users Guide Part V - Introductory Guide
- Chapter 4
Chapter 4 - Models for Population
Data
1. What This Chapter is About
In this chapter, models for data from (animal or
human) populations will be discussed. These models describe
observations from a number of individuals sampled from the
population. The distinguishing feature of the data to which
such models apply is that there is more than one
observation from some (usually most) individuals. A
population model includes the structural model of Chapter 3,
but also a new model, which shall be called the parameter
model, for each individual’s kinetic parameters.
The parameter model can have both fixed and random effects.
A population model also includes the error model of Chapter
3.
2. General
Individuals differ, and the types, degrees and
causes of these differences are often what we want to learn.
NONMEM was designed to help us learn these things. These
individual differences can be due to fixed and/or random
effects, but they all manifest themselves by affecting the
value of an individual’s parameters,
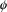 . That is, first, each
individual is regarded as having his own particular value of
. That is, first, each
individual is regarded as having his own particular value of
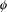 . If the data come from
. If the data come from
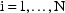 individuals, then we may
rewrite the (not completely) general mixed effects model,
(3.4) for
individuals, then we may
rewrite the (not completely) general mixed effects model,
(3.4) for  , the
, the
 observation from the
observation from the
 individual, as
individual, as

Eq (4.1) is now (part of) a population model
because it explicitly recognizes, through the subscript,
 , that the data come from
distinct individuals. Note too that we have written
, that the data come from
distinct individuals. Note too that we have written
 , rather than
, rather than
 . According to NONMEM
conventions, when modeling data from a population,
the random effects in the residual errors are denoted by
. According to NONMEM
conventions, when modeling data from a population,
the random effects in the residual errors are denoted by
 , their individual
variances by
, their individual
variances by 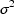 , and the
collection of the variances by the matrix
, and the
collection of the variances by the matrix
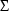 , denoted SIGMA in NONMEM
input and output. We also adopt the same convention here as
we did for
, denoted SIGMA in NONMEM
input and output. We also adopt the same convention here as
we did for  : the
: the
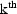 diagonal element of
diagonal element of
 is interchangeably denoted
is interchangeably denoted
 or
or
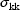 .
.
When dealing with population data, the symbol
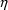 is reserved for random
effects influencing the vectors
is reserved for random
effects influencing the vectors
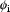 , as is now explained. We
can write a general model (but not yet as general a model as
we will present later) for
, as is now explained. We
can write a general model (but not yet as general a model as
we will present later) for 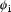 :
:

It is called the parameter model. Here,
 is a structural (though
non-kinetic) type model (of which examples will be given
shortly), which is a function of fixed effects,
is a structural (though
non-kinetic) type model (of which examples will be given
shortly), which is a function of fixed effects,
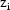 , and fixed effects
parameters,
, and fixed effects
parameters,  . Note that
since, in general,
. Note that
since, in general, 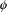 is a
vector,
is a
vector, 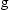 must be a
vector-valued function, and for the same reason,
must be a
vector-valued function, and for the same reason,
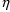 is usually a vector. This
will be discussed further later. All fixed effects, whether
they are part of the kinetic structural model, or are part
of the parameter model, are input to NONMEM in a uniform
way. For the purposes of this discussion, the symbol
is usually a vector. This
will be discussed further later. All fixed effects, whether
they are part of the kinetic structural model, or are part
of the parameter model, are input to NONMEM in a uniform
way. For the purposes of this discussion, the symbol
 is used for the particular
fixed effects in
is used for the particular
fixed effects in 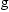 , such as
the individual’s height, weight, and so forth (this
will be discussed further in a moment). Even though most
often
, such as
the individual’s height, weight, and so forth (this
will be discussed further in a moment). Even though most
often 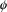 is regarded as time
invariant, as is done in most of the discussion in this
document, fixed effects can change with time, and thus
kinetic parameters within
is regarded as time
invariant, as is done in most of the discussion in this
document, fixed effects can change with time, and thus
kinetic parameters within  can change with time. This will be discussed further in
Section 3.4.2.
can change with time. This will be discussed further in
Section 3.4.2.
3. Structural Parameter Models
The symbol in (4.2) for the fixed effects
parameter vector is  , not
, not
 . As mentioned in Chapter
3, we reserve the symbol
. As mentioned in Chapter
3, we reserve the symbol 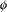 ,
in this document, for an individual’s fixed effect
parameters and use the symbol
,
in this document, for an individual’s fixed effect
parameters and use the symbol
 for a vector of
population (fixed effects and possibly random
effects) parameters.
for a vector of
population (fixed effects and possibly random
effects) parameters.
Recall the phenobarbital example of Chapter 2.
For the second run, the input contained the line of
code
TVCL = THETA(1) +
THETA(3)*WT
Translated into the symbols we are using here,
this is

In (4.3), 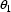 and
and
 are the first and third
elements of the parameter vector
are the first and third
elements of the parameter vector
 , and
, and
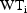 is an element of
is an element of
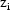 (recall that this value of
weight appears as a data item). The tilde over
(recall that this value of
weight appears as a data item). The tilde over
 is meant to distinguish
this typical population value of clearance from the
is meant to distinguish
this typical population value of clearance from the
 individual’s actual
value of clearance. According to this model,
individual’s actual
value of clearance. According to this model,
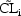 will be the same for any
two individuals both of whom have the same value of weight.
Equation (4.3) defines an element (the one associated with
clearance) of the vector-valued function
will be the same for any
two individuals both of whom have the same value of weight.
Equation (4.3) defines an element (the one associated with
clearance) of the vector-valued function
 . Note that in (4.3), we
use the subscript
. Note that in (4.3), we
use the subscript 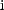 to stress
that this equation applies to the
to stress
that this equation applies to the
 individual, but there is no
confusion when, as in the NM-TRAN input, and in the
following, the subscript is omitted. It should always be
understood that all variables and data items used in the
parameter model definition refer to the same individual.
Many different models are possible to describe the
dependence of individual parameters on fixed effects.
However, certain model forms are simple, easy to use, and
cover most cases. An assortment of these will be discussed
briefly next.
individual, but there is no
confusion when, as in the NM-TRAN input, and in the
following, the subscript is omitted. It should always be
understood that all variables and data items used in the
parameter model definition refer to the same individual.
Many different models are possible to describe the
dependence of individual parameters on fixed effects.
However, certain model forms are simple, easy to use, and
cover most cases. An assortment of these will be discussed
briefly next.
3.1. Linear Models
The simplest form that
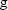 can take, and the most
common, is one that is linear in
can take, and the most
common, is one that is linear in
 . An example is (4.3): all
elements of
. An example is (4.3): all
elements of  appear as
linear coefficients of terms involving data items. The data
items themselves can appear nonlinearly, without affecting
the linearity with respect to
appear as
linear coefficients of terms involving data items. The data
items themselves can appear nonlinearly, without affecting
the linearity with respect to
 . For example, if clearance
is the sum of renal and non-renal components, and renal
clearance is believed to be proportional to renal function
as described according to a standard formula involving the
elements of
. For example, if clearance
is the sum of renal and non-renal components, and renal
clearance is believed to be proportional to renal function
as described according to a standard formula involving the
elements of  : age (
: age (
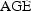 ), serum creatinine (
), serum creatinine (
 ), and weight (
), and weight (
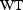 ), then one might
write
), then one might
write

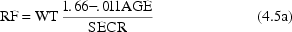


Clearly, 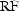 is a
nonlinear function of
is a
nonlinear function of 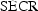 , for
example, and so, therefore, is
, for
example, and so, therefore, is
 , but
, but
 is linear in
is linear in
 , and (4.4 - 4.6) is still
considered a linear model. (Do not worry about the
non-consecutive numbering of the elements of
, and (4.4 - 4.6) is still
considered a linear model. (Do not worry about the
non-consecutive numbering of the elements of
 ; a model for
; a model for
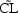 is being developed (an
alternative to 4.3), and the missing elements
is being developed (an
alternative to 4.3), and the missing elements
 and
and
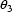 will appear
presently.)
will appear
presently.)
3.2. Multiplicative Models
Multiplicative models are linear models, but on a
logarithmic scale. For example, if patients covering a very
wide range of weights are studied, metabolic clearance might
vary with weight, but not linearly, and a substitute for
(4.4) might be
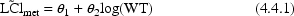

Note that the logarithm of
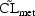 (
(
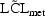 ) is linear in
) is linear in
 , but
, but
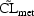 itself is not. Of course,
(4.4.1) can also be written
itself is not. Of course,
(4.4.1) can also be written

Models (4.4.1) and (4.4.2) are equivalent so far
as 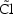 is concerned, but
is concerned, but
 of (4.4.2) corresponds to
of (4.4.2) corresponds to
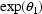 of (4.4.1).
of (4.4.1).
3.3. Saturation Models
A useful model for processes reaching a maximum
is a hyperbolic model. For example, if a second drug, (whose
steady-state plasma concentration,
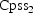 is known and available in
the data set), is present in some individuals and it is
believed that this second drug is an inhibitor of the
metabolism of the study drug, one might wish to
use
is known and available in
the data set), is present in some individuals and it is
believed that this second drug is an inhibitor of the
metabolism of the study drug, one might wish to
use

This model is shown in figure 4.1. The inhibition
is expressed by the ratio occurring within the brackets and
is a concave hyperbola, asymptoting to a maximum value equal
to 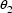 . It is identical in
form to the familiar Michaelis-Menten model. figure
+chapt4/fig4.1.ps height 2.5i bounds 54 450 378
693
. It is identical in
form to the familiar Michaelis-Menten model. figure
+chapt4/fig4.1.ps height 2.5i bounds 54 450 378
693
3.4. Models with Indicator Variables
Indicator variables were discussed in Chapter 3
in connection with the error model. They can be quite useful
when modelling individual parameters. They are usually used
in a linear model. For example, if the clinical condition,
heart failure, is noted as "present" or
"absent", one can define an indicator variable,
 which equals 0 if heart
failure is absent, and 1 if it is present. If metabolic
clearance is thought to be affected by heart failure, one
might choose
which equals 0 if heart
failure is absent, and 1 if it is present. If metabolic
clearance is thought to be affected by heart failure, one
might choose
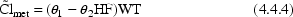
Here, the non-heart-failure cases will have
 , while the heart-failure
cases will have
, while the heart-failure
cases will have 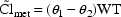 †.
†.
----------

3.4.1. Combinations
Given the basic building blocks of linear,
multiplicative and saturation models, these can be combined
in the usual algebraic ways (usually by addition) to make
more complex models. For example, one could use (4.4.3),
(4.5), and (4.6) as a model for
 . A non-additive example
arises if plasma and urine concentrations are both observed
and (kinetic) model (3.6) is to be used for the latter. The
parameter
. A non-additive example
arises if plasma and urine concentrations are both observed
and (kinetic) model (3.6) is to be used for the latter. The
parameter  , the fraction of
drug excreted unchanged into the urine might be modeled
as
, the fraction of
drug excreted unchanged into the urine might be modeled
as

where  is given
by (4.5) and
is given
by (4.5) and 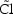 by (4.6)
(using any of the (4.4) variants).
by (4.6)
(using any of the (4.4) variants).
3.4.2. Time Varying 
As mentioned in Section 2, although most of the
time the data items affecting an individual’s
 do not change over the
course of his data, they occasionally do, and PREDPP can
handle this. For example, if an individual had heart failure
for part of his observation period, but not the rest,
do not change over the
course of his data, they occasionally do, and PREDPP can
handle this. For example, if an individual had heart failure
for part of his observation period, but not the rest,
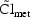 , according to (4.4.4)
should change. Or, if acute renal failure occurred during a
patient’s observation period,
, according to (4.4.4)
should change. Or, if acute renal failure occurred during a
patient’s observation period,
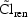 would change, according to
model (4.5).
would change, according to
model (4.5).
PREDPP implements its kinetic model recursively:
given the state of the system at time
 (by state we mean the
amounts of drug in all the compartments), it updates (i.e.
advances) the state to that at time
(by state we mean the
amounts of drug in all the compartments), it updates (i.e.
advances) the state to that at time
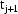 , using the value of
, using the value of
 (and in general, the value
of
(and in general, the value
of  ) at time
) at time
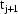 to compute a value of
to compute a value of
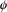 holding between times
holding between times
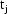 and
and
 . The value of
. The value of
 used to compute this
used to compute this
 is that value found on the
data record with time
is that value found on the
data record with time 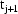 .
So, in order to have
.
So, in order to have 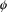 change appropriately as
change appropriately as  does, one places a value of
does, one places a value of
 which is typical for the
time period
which is typical for the
time period  to
to
 on the data record
associated with the time point
on the data record
associated with the time point
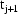 . This will not always be
easy since the relevant element(s) of
. This will not always be
easy since the relevant element(s) of
 may not be measured at,
for example, the midpoint of the time interval (the value at
the
may not be measured at,
for example, the midpoint of the time interval (the value at
the  of the time interval
is a good choice for the
of the time interval
is a good choice for the 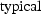 value for the interval). If not, one will have to use some
interpolation method to arrive at the typical value. The
important point is that the values of the independent
variables at time
value for the interval). If not, one will have to use some
interpolation method to arrive at the typical value. The
important point is that the values of the independent
variables at time 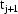 determine the values of the individual’s parameters
applying to the entire period
determine the values of the individual’s parameters
applying to the entire period
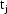 to
to
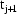 .
.
3.5. Structural Kinetic Models
The kinetic models (i.e., the models for
responses such as drug concentrations) used when performing
a population analysis do not differ at all from those used
for an individual analysis. One still needs a model for the
relationship of  to
to
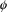 and
and
 , and this relationship
does not depend on whether
, and this relationship
does not depend on whether 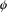 changes from individual to individual or with time within an
individual.
changes from individual to individual or with time within an
individual.
4. Population Random Effects Models
Under NONMEM conventions, there are two levels of
random effects, and  and
and
 are the symbols used for
the vectors of first and second level random effects,
respectively. With data from a single individual, only
first-level random effects are needed. However, with data
from a population of individuals, both first- and
second-level random effects are needed. First-level effects
are needed in the parameter model to help model
unexplainable interindividual differences in
are the symbols used for
the vectors of first and second level random effects,
respectively. With data from a single individual, only
first-level random effects are needed. However, with data
from a population of individuals, both first- and
second-level random effects are needed. First-level effects
are needed in the parameter model to help model
unexplainable interindividual differences in
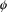 , and second-level effects
are needed in the (intraindividual) error model. For
example, in (4.2) there is an element of
, and second-level effects
are needed in the (intraindividual) error model. For
example, in (4.2) there is an element of
 ,
,
 , that is the difference
between the individual value
, that is the difference
between the individual value
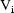 (an element of
(an element of
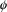 ) and
) and
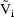 , the typical value of
, the typical value of
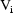 . This is a first-level
random effect. In (4.1)
. This is a first-level
random effect. In (4.1)  is
the error between
is
the error between 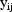 and
and
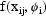 . This is a second-level
random effect.
. This is a second-level
random effect.
4.1. Models for Interindividual Errors
The difference between
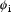 and
and
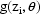 is called an
interindividual error. It arises from a few sources:
the function
is called an
interindividual error. It arises from a few sources:
the function  may be only
approximate, and/or
may be only
approximate, and/or  may be
measured with error. It is regarded as a random quantity,
and it may be modeled in terms of
may be
measured with error. It is regarded as a random quantity,
and it may be modeled in terms of
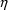 variables. As usual, each
of these variables is assumed to have mean 0 and a variance
denoted by
variables. As usual, each
of these variables is assumed to have mean 0 and a variance
denoted by  which may be
estimated. This variance describes biological population
variability.
which may be
estimated. This variance describes biological population
variability.
The difference between
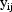 and
and
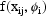 is called an
intraindividual error. It has been discussed at some
length in Chapter 3. Although in that discussion about
individual data, this difference was modeled in terms of
is called an
intraindividual error. It has been discussed at some
length in Chapter 3. Although in that discussion about
individual data, this difference was modeled in terms of
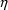 variables, in this
discussion about population data, it is modeled in terms of
variables, in this
discussion about population data, it is modeled in terms of
 variables. Each
variables. Each
 variable is assumed to
have mean 0 and a variance denoted by
variable is assumed to
have mean 0 and a variance denoted by
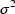 which also may be
estimated.
which also may be
estimated.
Each pair of elements in
 has a covariance, and
NONMEM can also estimate this, although often we choose to
assume that the covariance is zero (we made this same
assumption for the different elements of
has a covariance, and
NONMEM can also estimate this, although often we choose to
assume that the covariance is zero (we made this same
assumption for the different elements of
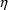 in Chapter 3, Section
3.7). A covariance between two elements of
in Chapter 3, Section
3.7). A covariance between two elements of
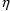 ,
,
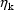 and
and
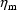 , say, is a measure of
statistical association between these two random variables.
Their covariance is related to their correlation,
, say, is a measure of
statistical association between these two random variables.
Their covariance is related to their correlation,
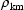 (
(
 ) by
) by

(Note that now that we are suppressing the
subscript 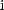 on
on
 , we may, without
confusion, use the subscript position to designate elements
of
, we may, without
confusion, use the subscript position to designate elements
of  .)
.)
The variances and covariances among the elements
of  are laid out in a
covariance matrix, called
are laid out in a
covariance matrix, called
 , and labeled OMEGA in
NONMEM input and output. This matrix was defined in Chapter
3, Section 3.7, but some additional comment here may be
helpful. If
, and labeled OMEGA in
NONMEM input and output. This matrix was defined in Chapter
3, Section 3.7, but some additional comment here may be
helpful. If 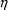 has, for
example, 3 elements,
has, for
example, 3 elements,  has
the following form:
has
the following form:
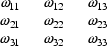
Here, as previously, 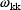 is another way of writing the variance
is another way of writing the variance
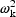 , and
, and
 (
(
 ) is the covariance
between
) is the covariance
between 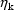 and
and
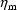 .
.
The elements  ,
,
 ,
,
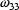 are called the diagonal
elements of the matrix. If the nondiagonal elements (the
covariances) are all zero, i.e. the correlation among all
pairs of
are called the diagonal
elements of the matrix. If the nondiagonal elements (the
covariances) are all zero, i.e. the correlation among all
pairs of 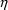 elements is zero,
the matrix is called a diagonal matrix. The lower
triangular elements of the matrix are the elements
elements is zero,
the matrix is called a diagonal matrix. The lower
triangular elements of the matrix are the elements
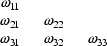
To specify the matrix only its lower triangular elements
need be given (and these are all NONMEM does give), since
from (4.8) it is clear that for all
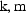 ,
,
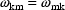 .
.
4.1.1. Additive/Multiplicative Models
Frequently, the model for an interindividual error is
the simple additive one (as in (4.2)), such as

A feature of (4.9) is that the resulting units for
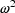 depend on the units of the
parameter (
depend on the units of the
parameter (  in this case).
For example, this model was used in the theophylline problem
of Chapter 2 (Figure 2.6). The final estimate of
in this case).
For example, this model was used in the theophylline problem
of Chapter 2 (Figure 2.6). The final estimate of
 is .286 (Figure 2.8).
Assuming that the units of V are liters, we interpret this
to mean that the standard deviation of V between individuals
is .53 Liters ( .53 =
is .286 (Figure 2.8).
Assuming that the units of V are liters, we interpret this
to mean that the standard deviation of V between individuals
is .53 Liters ( .53 =  ).
).
Perhaps even more often, a multiplicative model
equivalent to the Constant Coefficient of Variation (CCV)
error model (3.5) is used, such as

A feature of (4.10) is that the resulting units for
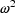 are independent of the
units of the parameter (
are independent of the
units of the parameter ( 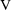 in this case). When this model is used in the theophylline
problem instead of the additive model, so that Figure 2.6
contains the code V=TVVD*(1+ETA(2)) instead of
V=TVVD+ETA(2), then NONMEM estimates
in this case). When this model is used in the theophylline
problem instead of the additive model, so that Figure 2.6
contains the code V=TVVD*(1+ETA(2)) instead of
V=TVVD+ETA(2), then NONMEM estimates
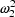 to be .146. We interpret
this to mean that the coefficient of variation of V in the
population is 38% (.38 =
to be .146. We interpret
this to mean that the coefficient of variation of V in the
population is 38% (.38 =  ).
).
4.1.2. Other Models
Occasionally, a model for an individual’s
pharmacokinetic parameter might involve scaling an
 , as in (3.6), or two or
more
, as in (3.6), or two or
more 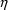 ’s as in
(3.10). For example, a study might involve patients in the
intensive care unit (ICU) and others on non-acute care
units. It might be reasonable to suppose that some aspects
of the kinetics of ICU patients (e.g., metabolic clearance
of drug) are more variable, due to unmeasured factors (e.g.,
hepatic function) that vary greatly among acutely ill
patients. Even though the variation is, in reality, due to a
potentially measurable fixed effect (hepatic function), if
information on this fixed effect is not available,
differences caused by it must be assigned to random factors
(
’s as in
(3.10). For example, a study might involve patients in the
intensive care unit (ICU) and others on non-acute care
units. It might be reasonable to suppose that some aspects
of the kinetics of ICU patients (e.g., metabolic clearance
of drug) are more variable, due to unmeasured factors (e.g.,
hepatic function) that vary greatly among acutely ill
patients. Even though the variation is, in reality, due to a
potentially measurable fixed effect (hepatic function), if
information on this fixed effect is not available,
differences caused by it must be assigned to random factors
( 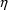 ). In this case, one
might wish to use an indicator variable,
). In this case, one
might wish to use an indicator variable,
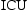 (which equals 1 if the
patient is in the ICU, and 0, otherwise), and a model such
as
(which equals 1 if the
patient is in the ICU, and 0, otherwise), and a model such
as
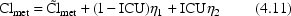
In addition to model (4.11) we might have, for
example,


Models (4.11) and (4.12) together, along with suitable
models for  and
and
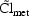 , form a complete model
for an individual’s
, form a complete model
for an individual’s  parameter, and involve 3
parameter, and involve 3 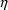 ’s.
’s.
4.1.3. General Form for the Parameter Model
As we have just seen in (4.10) and in (4.11)-(4.12), an
element of 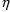 need not act in
a simple additive way and may act solely on an intermediate
variable (e.g.
need not act in
a simple additive way and may act solely on an intermediate
variable (e.g. 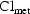 ). Indeed,
there may be more or fewer elements in
). Indeed,
there may be more or fewer elements in
 than in
than in
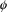 , the elements in
, the elements in
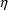 may act in nonlinear ways
to influence
may act in nonlinear ways
to influence  , and one
element of
, and one
element of 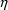 may influence
more than a single element of
may influence
more than a single element of
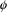 . We now give a more
general form for the parameter model than (4.2) and then an
example illustrating it.
. We now give a more
general form for the parameter model than (4.2) and then an
example illustrating it.
The general form of the parameter model is

Here, 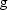 is a very
general function of fixed effects,
is a very
general function of fixed effects,
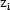 , fixed effects
parameters,
, fixed effects
parameters,  , and a vector
of
, and a vector
of 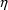 ’s,
’s,
 . The dimensions of the
vectors
. The dimensions of the
vectors 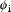 and
and
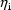 need not be the same. An
individual’s kinetic parameter may change with time.
As explained in Section 1.6, with NONMEM-PREDPP changes can
occur only at discrete time points. Therefore, the parameter
actually can be regarded as being a number of parameters,
each one applying to a different time period. The parameter
need not be the same. An
individual’s kinetic parameter may change with time.
As explained in Section 1.6, with NONMEM-PREDPP changes can
occur only at discrete time points. Therefore, the parameter
actually can be regarded as being a number of parameters,
each one applying to a different time period. The parameter
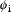 in (4.13), being a vector
of all the kinetic parameters for the
in (4.13), being a vector
of all the kinetic parameters for the
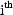 individual, can be
regarded as encompassing these time-interval-specific
parameters.
individual, can be
regarded as encompassing these time-interval-specific
parameters.
An example utilizing this generality is provided by a
model for observations of both plasma and urine drug
concentrations, similar to the one presented previously.
Ignoring the details of the structural part of the model,
consider the following model
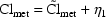
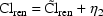

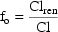
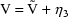
In this model, 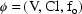 ; the
parameters
; the
parameters  and
and
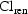 are regarded as
intermediate parameters. We have
are regarded as
intermediate parameters. We have
 , where both
, where both
 and
and
 influence both
influence both
 (linearly) and
(linearly) and
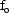 (nonlinearly).
(nonlinearly).
4.2. Statistical Models for an Individual’s Observations
Model (4.1) can be generalized by incorporating a model
like those given in Chapter 3 for the residual errors, i.e.
for the differences between the
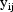 and
and
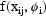 , rather than using just
the simple Additive model. A particular instance of such a
model may have several types of
, rather than using just
the simple Additive model. A particular instance of such a
model may have several types of
 ’s, and as mentioned
in Section 2, the variances of these
’s, and as mentioned
in Section 2, the variances of these
 ’s are denoted by
’s are denoted by
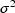 ’s. With a
population model these variances could change from
individual to individual. With NONMEM, they are considered
as constants over individuals. The
’s. With a
population model these variances could change from
individual to individual. With NONMEM, they are considered
as constants over individuals. The
 ’s can co-vary. A
covariance matrix
’s can co-vary. A
covariance matrix  , like
the
, like
the  matrix given in
Section 4.1, gives the variances and covariances of the
matrix given in
Section 4.1, gives the variances and covariances of the
 ’s, as already
discussed at the end of Chapter 3. This does not preclude
the magnitudes of the errors from being affected by fixed
effects. A model such as (3.8) can still be used. This is
shown explicitly by the general model given in the next
section.
’s, as already
discussed at the end of Chapter 3. This does not preclude
the magnitudes of the errors from being affected by fixed
effects. A model such as (3.8) can still be used. This is
shown explicitly by the general model given in the next
section.
5. The Population Mixed Effects Model
We have now presented all of the parts needed to fully
define a population model. It may be useful to recap this
information by stating the entire general model here:
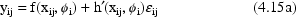

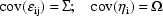
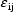 ,
,
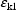 independent for
independent for
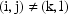
 ,
,
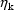 independent for
independent for
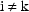
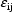 ,
,
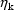 independent for all
independent for all
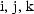 ,
,
where here, 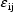 is a
vector, along with
is a
vector, along with 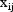 ,
,
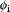 ,
,
 and
and
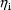 , and
, and
 and
and
 are square matrices with
dimensions equal to those of
are square matrices with
dimensions equal to those of
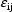 and
and
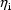 .
.
To try to represent the relationship between all the
fixed and random effects of a population model graphically,
consider figure 4.2. The model corresponding to this figure
is
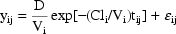

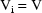
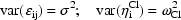
where the  are all
equal to a constant
are all
equal to a constant 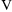 , i.e.
there is no random interindividual variability in the volume
of distribution, so that for the sake of this example,
, i.e.
there is no random interindividual variability in the volume
of distribution, so that for the sake of this example,
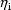 is just a scalar.
is just a scalar.
TOP
TABLE OF CONTENTS
NEXT
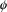 . That is, first, each
individual is regarded as having his own particular value of
. That is, first, each
individual is regarded as having his own particular value of
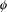 . If the data come from
. If the data come from
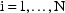 individuals, then we may
rewrite the (not completely) general mixed effects model,
(3.4) for
individuals, then we may
rewrite the (not completely) general mixed effects model,
(3.4) for  , the
, the
 observation from the
observation from the
 individual, as
individual, as

 , that the data come from
distinct individuals. Note too that we have written
, that the data come from
distinct individuals. Note too that we have written
 , rather than
, rather than
 . According to NONMEM
conventions, when modeling data from a population,
the random effects in the residual errors are denoted by
. According to NONMEM
conventions, when modeling data from a population,
the random effects in the residual errors are denoted by
 , their individual
variances by
, their individual
variances by 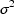 , and the
collection of the variances by the matrix
, and the
collection of the variances by the matrix
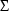 , denoted SIGMA in NONMEM
input and output. We also adopt the same convention here as
we did for
, denoted SIGMA in NONMEM
input and output. We also adopt the same convention here as
we did for  : the
: the
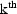 diagonal element of
diagonal element of
 is interchangeably denoted
is interchangeably denoted
 or
or
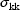 .
.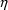 is reserved for random
effects influencing the vectors
is reserved for random
effects influencing the vectors
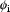 , as is now explained. We
can write a general model (but not yet as general a model as
we will present later) for
, as is now explained. We
can write a general model (but not yet as general a model as
we will present later) for 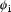 :
:
 is a structural (though
non-kinetic) type model (of which examples will be given
shortly), which is a function of fixed effects,
is a structural (though
non-kinetic) type model (of which examples will be given
shortly), which is a function of fixed effects,
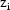 , and fixed effects
parameters,
, and fixed effects
parameters,  . Note that
since, in general,
. Note that
since, in general, 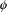 is a
vector,
is a
vector, 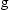 must be a
vector-valued function, and for the same reason,
must be a
vector-valued function, and for the same reason,
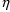 is usually a vector. This
will be discussed further later. All fixed effects, whether
they are part of the kinetic structural model, or are part
of the parameter model, are input to NONMEM in a uniform
way. For the purposes of this discussion, the symbol
is usually a vector. This
will be discussed further later. All fixed effects, whether
they are part of the kinetic structural model, or are part
of the parameter model, are input to NONMEM in a uniform
way. For the purposes of this discussion, the symbol
 is used for the particular
fixed effects in
is used for the particular
fixed effects in 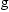 , such as
the individual’s height, weight, and so forth (this
will be discussed further in a moment). Even though most
often
, such as
the individual’s height, weight, and so forth (this
will be discussed further in a moment). Even though most
often 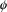 is regarded as time
invariant, as is done in most of the discussion in this
document, fixed effects can change with time, and thus
kinetic parameters within
is regarded as time
invariant, as is done in most of the discussion in this
document, fixed effects can change with time, and thus
kinetic parameters within  can change with time. This will be discussed further in
Section 3.4.2.
can change with time. This will be discussed further in
Section 3.4.2. , not
, not
 . As mentioned in Chapter
3, we reserve the symbol
. As mentioned in Chapter
3, we reserve the symbol 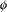 ,
in this document, for an individual’s fixed effect
parameters and use the symbol
,
in this document, for an individual’s fixed effect
parameters and use the symbol
 for a vector of
population (fixed effects and possibly random
effects) parameters.
for a vector of
population (fixed effects and possibly random
effects) parameters.
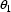 and
and
 are the first and third
elements of the parameter vector
are the first and third
elements of the parameter vector
 , and
, and
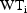 is an element of
is an element of
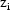 (recall that this value of
weight appears as a data item). The tilde over
(recall that this value of
weight appears as a data item). The tilde over
 is meant to distinguish
this typical population value of clearance from the
is meant to distinguish
this typical population value of clearance from the
 individual’s actual
value of clearance. According to this model,
individual’s actual
value of clearance. According to this model,
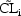 will be the same for any
two individuals both of whom have the same value of weight.
Equation (4.3) defines an element (the one associated with
clearance) of the vector-valued function
will be the same for any
two individuals both of whom have the same value of weight.
Equation (4.3) defines an element (the one associated with
clearance) of the vector-valued function
 . Note that in (4.3), we
use the subscript
. Note that in (4.3), we
use the subscript 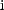 to stress
that this equation applies to the
to stress
that this equation applies to the
 individual, but there is no
confusion when, as in the NM-TRAN input, and in the
following, the subscript is omitted. It should always be
understood that all variables and data items used in the
parameter model definition refer to the same individual.
Many different models are possible to describe the
dependence of individual parameters on fixed effects.
However, certain model forms are simple, easy to use, and
cover most cases. An assortment of these will be discussed
briefly next.
individual, but there is no
confusion when, as in the NM-TRAN input, and in the
following, the subscript is omitted. It should always be
understood that all variables and data items used in the
parameter model definition refer to the same individual.
Many different models are possible to describe the
dependence of individual parameters on fixed effects.
However, certain model forms are simple, easy to use, and
cover most cases. An assortment of these will be discussed
briefly next.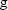 can take, and the most
common, is one that is linear in
can take, and the most
common, is one that is linear in
 . An example is (4.3): all
elements of
. An example is (4.3): all
elements of  appear as
linear coefficients of terms involving data items. The data
items themselves can appear nonlinearly, without affecting
the linearity with respect to
appear as
linear coefficients of terms involving data items. The data
items themselves can appear nonlinearly, without affecting
the linearity with respect to
 . For example, if clearance
is the sum of renal and non-renal components, and renal
clearance is believed to be proportional to renal function
as described according to a standard formula involving the
elements of
. For example, if clearance
is the sum of renal and non-renal components, and renal
clearance is believed to be proportional to renal function
as described according to a standard formula involving the
elements of  : age (
: age (
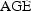 ), serum creatinine (
), serum creatinine (
 ), and weight (
), and weight (
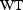 ), then one might
write
), then one might
write
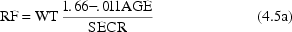


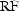 is a
nonlinear function of
is a
nonlinear function of 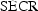 , for
example, and so, therefore, is
, for
example, and so, therefore, is
 , but
, but
 is linear in
is linear in
 , and (4.4 - 4.6) is still
considered a linear model. (Do not worry about the
non-consecutive numbering of the elements of
, and (4.4 - 4.6) is still
considered a linear model. (Do not worry about the
non-consecutive numbering of the elements of
 ; a model for
; a model for
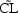 is being developed (an
alternative to 4.3), and the missing elements
is being developed (an
alternative to 4.3), and the missing elements
 and
and
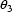 will appear
presently.)
will appear
presently.)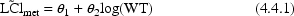

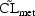 (
(
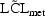 ) is linear in
) is linear in
 , but
, but
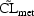 itself is not. Of course,
(4.4.1) can also be written
itself is not. Of course,
(4.4.1) can also be written
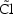 is concerned, but
is concerned, but
 of (4.4.2) corresponds to
of (4.4.2) corresponds to
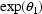 of (4.4.1).
of (4.4.1).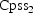 is known and available in
the data set), is present in some individuals and it is
believed that this second drug is an inhibitor of the
metabolism of the study drug, one might wish to
use
is known and available in
the data set), is present in some individuals and it is
believed that this second drug is an inhibitor of the
metabolism of the study drug, one might wish to
use
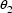 . It is identical in
form to the familiar Michaelis-Menten model. figure
+chapt4/fig4.1.ps height 2.5i bounds 54 450 378
693
. It is identical in
form to the familiar Michaelis-Menten model. figure
+chapt4/fig4.1.ps height 2.5i bounds 54 450 378
693 which equals 0 if heart
failure is absent, and 1 if it is present. If metabolic
clearance is thought to be affected by heart failure, one
might choose
which equals 0 if heart
failure is absent, and 1 if it is present. If metabolic
clearance is thought to be affected by heart failure, one
might choose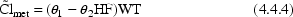
 , while the heart-failure
cases will have
, while the heart-failure
cases will have 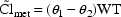 †.
†.
 . A non-additive example
arises if plasma and urine concentrations are both observed
and (kinetic) model (3.6) is to be used for the latter. The
parameter
. A non-additive example
arises if plasma and urine concentrations are both observed
and (kinetic) model (3.6) is to be used for the latter. The
parameter  , the fraction of
drug excreted unchanged into the urine might be modeled
as
, the fraction of
drug excreted unchanged into the urine might be modeled
as
 is given
by (4.5) and
is given
by (4.5) and 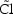 by (4.6)
(using any of the (4.4) variants).
by (4.6)
(using any of the (4.4) variants). do not change over the
course of his data, they occasionally do, and PREDPP can
handle this. For example, if an individual had heart failure
for part of his observation period, but not the rest,
do not change over the
course of his data, they occasionally do, and PREDPP can
handle this. For example, if an individual had heart failure
for part of his observation period, but not the rest,
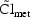 , according to (4.4.4)
should change. Or, if acute renal failure occurred during a
patient’s observation period,
, according to (4.4.4)
should change. Or, if acute renal failure occurred during a
patient’s observation period,
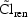 would change, according to
model (4.5).
would change, according to
model (4.5). (by state we mean the
amounts of drug in all the compartments), it updates (i.e.
advances) the state to that at time
(by state we mean the
amounts of drug in all the compartments), it updates (i.e.
advances) the state to that at time
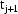 , using the value of
, using the value of
 (and in general, the value
of
(and in general, the value
of  ) at time
) at time
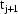 to compute a value of
to compute a value of
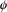 holding between times
holding between times
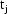 and
and
 . The value of
. The value of
 used to compute this
used to compute this
 is that value found on the
data record with time
is that value found on the
data record with time 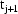 .
So, in order to have
.
So, in order to have 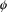 change appropriately as
change appropriately as  does, one places a value of
does, one places a value of
 which is typical for the
time period
which is typical for the
time period  to
to
 on the data record
associated with the time point
on the data record
associated with the time point
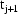 . This will not always be
easy since the relevant element(s) of
. This will not always be
easy since the relevant element(s) of
 may not be measured at,
for example, the midpoint of the time interval (the value at
the
may not be measured at,
for example, the midpoint of the time interval (the value at
the  of the time interval
is a good choice for the
of the time interval
is a good choice for the 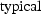 value for the interval). If not, one will have to use some
interpolation method to arrive at the typical value. The
important point is that the values of the independent
variables at time
value for the interval). If not, one will have to use some
interpolation method to arrive at the typical value. The
important point is that the values of the independent
variables at time 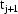 determine the values of the individual’s parameters
applying to the entire period
determine the values of the individual’s parameters
applying to the entire period
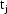 to
to
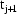 .
. to
to
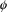 and
and
 , and this relationship
does not depend on whether
, and this relationship
does not depend on whether 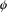 changes from individual to individual or with time within an
individual.
changes from individual to individual or with time within an
individual. and
and
 are the symbols used for
the vectors of first and second level random effects,
respectively. With data from a single individual, only
first-level random effects are needed. However, with data
from a population of individuals, both first- and
second-level random effects are needed. First-level effects
are needed in the parameter model to help model
unexplainable interindividual differences in
are the symbols used for
the vectors of first and second level random effects,
respectively. With data from a single individual, only
first-level random effects are needed. However, with data
from a population of individuals, both first- and
second-level random effects are needed. First-level effects
are needed in the parameter model to help model
unexplainable interindividual differences in
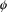 , and second-level effects
are needed in the (intraindividual) error model. For
example, in (4.2) there is an element of
, and second-level effects
are needed in the (intraindividual) error model. For
example, in (4.2) there is an element of
 ,
,
 , that is the difference
between the individual value
, that is the difference
between the individual value
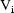 (an element of
(an element of
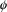 ) and
) and
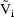 , the typical value of
, the typical value of
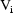 . This is a first-level
random effect. In (4.1)
. This is a first-level
random effect. In (4.1)  is
the error between
is
the error between 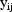 and
and
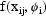 . This is a second-level
random effect.
. This is a second-level
random effect.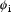 and
and
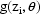 is called an
interindividual error. It arises from a few sources:
the function
is called an
interindividual error. It arises from a few sources:
the function  may be only
approximate, and/or
may be only
approximate, and/or  may be
measured with error. It is regarded as a random quantity,
and it may be modeled in terms of
may be
measured with error. It is regarded as a random quantity,
and it may be modeled in terms of
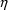 variables. As usual, each
of these variables is assumed to have mean 0 and a variance
denoted by
variables. As usual, each
of these variables is assumed to have mean 0 and a variance
denoted by  which may be
estimated. This variance describes biological population
variability.
which may be
estimated. This variance describes biological population
variability.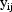 and
and
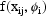 is called an
intraindividual error. It has been discussed at some
length in Chapter 3. Although in that discussion about
individual data, this difference was modeled in terms of
is called an
intraindividual error. It has been discussed at some
length in Chapter 3. Although in that discussion about
individual data, this difference was modeled in terms of
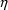 variables, in this
discussion about population data, it is modeled in terms of
variables, in this
discussion about population data, it is modeled in terms of
 variables. Each
variables. Each
 variable is assumed to
have mean 0 and a variance denoted by
variable is assumed to
have mean 0 and a variance denoted by
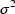 which also may be
estimated.
which also may be
estimated. has a covariance, and
NONMEM can also estimate this, although often we choose to
assume that the covariance is zero (we made this same
assumption for the different elements of
has a covariance, and
NONMEM can also estimate this, although often we choose to
assume that the covariance is zero (we made this same
assumption for the different elements of
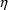 in Chapter 3, Section
3.7). A covariance between two elements of
in Chapter 3, Section
3.7). A covariance between two elements of
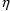 ,
,
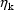 and
and
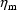 , say, is a measure of
statistical association between these two random variables.
Their covariance is related to their correlation,
, say, is a measure of
statistical association between these two random variables.
Their covariance is related to their correlation,
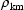 (
(
 ) by
) by
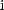 on
on
 , we may, without
confusion, use the subscript position to designate elements
of
, we may, without
confusion, use the subscript position to designate elements
of  .)
.) are laid out in a
covariance matrix, called
are laid out in a
covariance matrix, called
 , and labeled OMEGA in
NONMEM input and output. This matrix was defined in Chapter
3, Section 3.7, but some additional comment here may be
helpful. If
, and labeled OMEGA in
NONMEM input and output. This matrix was defined in Chapter
3, Section 3.7, but some additional comment here may be
helpful. If 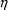 has, for
example, 3 elements,
has, for
example, 3 elements,  has
the following form:
has
the following form: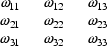
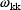 is another way of writing the variance
is another way of writing the variance
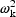 , and
, and
 (
(
 ) is the covariance
between
) is the covariance
between 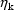 and
and
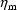 .
. ,
,
 ,
,
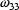 are called the diagonal
elements of the matrix. If the nondiagonal elements (the
covariances) are all zero, i.e. the correlation among all
pairs of
are called the diagonal
elements of the matrix. If the nondiagonal elements (the
covariances) are all zero, i.e. the correlation among all
pairs of 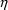 elements is zero,
the matrix is called a diagonal matrix. The lower
triangular elements of the matrix are the elements
elements is zero,
the matrix is called a diagonal matrix. The lower
triangular elements of the matrix are the elements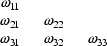
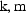 ,
,
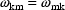 .
.
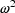 depend on the units of the
parameter (
depend on the units of the
parameter (  in this case).
For example, this model was used in the theophylline problem
of Chapter 2 (Figure 2.6). The final estimate of
in this case).
For example, this model was used in the theophylline problem
of Chapter 2 (Figure 2.6). The final estimate of
 is .286 (Figure 2.8).
Assuming that the units of V are liters, we interpret this
to mean that the standard deviation of V between individuals
is .53 Liters ( .53 =
is .286 (Figure 2.8).
Assuming that the units of V are liters, we interpret this
to mean that the standard deviation of V between individuals
is .53 Liters ( .53 =  ).
).
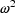 are independent of the
units of the parameter (
are independent of the
units of the parameter ( 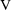 in this case). When this model is used in the theophylline
problem instead of the additive model, so that Figure 2.6
contains the code V=TVVD*(1+ETA(2)) instead of
V=TVVD+ETA(2), then NONMEM estimates
in this case). When this model is used in the theophylline
problem instead of the additive model, so that Figure 2.6
contains the code V=TVVD*(1+ETA(2)) instead of
V=TVVD+ETA(2), then NONMEM estimates
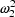 to be .146. We interpret
this to mean that the coefficient of variation of V in the
population is 38% (.38 =
to be .146. We interpret
this to mean that the coefficient of variation of V in the
population is 38% (.38 =  ).
). , as in (3.6), or two or
more
, as in (3.6), or two or
more 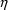 ’s as in
(3.10). For example, a study might involve patients in the
intensive care unit (ICU) and others on non-acute care
units. It might be reasonable to suppose that some aspects
of the kinetics of ICU patients (e.g., metabolic clearance
of drug) are more variable, due to unmeasured factors (e.g.,
hepatic function) that vary greatly among acutely ill
patients. Even though the variation is, in reality, due to a
potentially measurable fixed effect (hepatic function), if
information on this fixed effect is not available,
differences caused by it must be assigned to random factors
(
’s as in
(3.10). For example, a study might involve patients in the
intensive care unit (ICU) and others on non-acute care
units. It might be reasonable to suppose that some aspects
of the kinetics of ICU patients (e.g., metabolic clearance
of drug) are more variable, due to unmeasured factors (e.g.,
hepatic function) that vary greatly among acutely ill
patients. Even though the variation is, in reality, due to a
potentially measurable fixed effect (hepatic function), if
information on this fixed effect is not available,
differences caused by it must be assigned to random factors
( 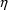 ). In this case, one
might wish to use an indicator variable,
). In this case, one
might wish to use an indicator variable,
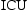 (which equals 1 if the
patient is in the ICU, and 0, otherwise), and a model such
as
(which equals 1 if the
patient is in the ICU, and 0, otherwise), and a model such
as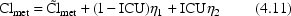


 and
and
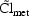 , form a complete model
for an individual’s
, form a complete model
for an individual’s  parameter, and involve 3
parameter, and involve 3 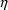 ’s.
’s.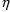 need not act in
a simple additive way and may act solely on an intermediate
variable (e.g.
need not act in
a simple additive way and may act solely on an intermediate
variable (e.g. 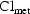 ). Indeed,
there may be more or fewer elements in
). Indeed,
there may be more or fewer elements in
 than in
than in
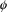 , the elements in
, the elements in
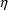 may act in nonlinear ways
to influence
may act in nonlinear ways
to influence  , and one
element of
, and one
element of 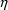 may influence
more than a single element of
may influence
more than a single element of
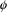 . We now give a more
general form for the parameter model than (4.2) and then an
example illustrating it.
. We now give a more
general form for the parameter model than (4.2) and then an
example illustrating it.
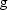 is a very
general function of fixed effects,
is a very
general function of fixed effects,
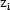 , fixed effects
parameters,
, fixed effects
parameters,  , and a vector
of
, and a vector
of 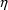 ’s,
’s,
 . The dimensions of the
vectors
. The dimensions of the
vectors 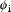 and
and
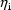 need not be the same. An
individual’s kinetic parameter may change with time.
As explained in Section 1.6, with NONMEM-PREDPP changes can
occur only at discrete time points. Therefore, the parameter
actually can be regarded as being a number of parameters,
each one applying to a different time period. The parameter
need not be the same. An
individual’s kinetic parameter may change with time.
As explained in Section 1.6, with NONMEM-PREDPP changes can
occur only at discrete time points. Therefore, the parameter
actually can be regarded as being a number of parameters,
each one applying to a different time period. The parameter
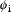 in (4.13), being a vector
of all the kinetic parameters for the
in (4.13), being a vector
of all the kinetic parameters for the
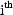 individual, can be
regarded as encompassing these time-interval-specific
parameters.
individual, can be
regarded as encompassing these time-interval-specific
parameters.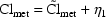
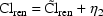

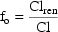
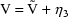
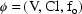 ; the
parameters
; the
parameters  and
and
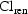 are regarded as
intermediate parameters. We have
are regarded as
intermediate parameters. We have
 , where both
, where both
 and
and
 influence both
influence both
 (linearly) and
(linearly) and
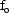 (nonlinearly).
(nonlinearly).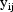 and
and
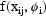 , rather than using just
the simple Additive model. A particular instance of such a
model may have several types of
, rather than using just
the simple Additive model. A particular instance of such a
model may have several types of
 ’s, and as mentioned
in Section 2, the variances of these
’s, and as mentioned
in Section 2, the variances of these
 ’s are denoted by
’s are denoted by
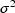 ’s. With a
population model these variances could change from
individual to individual. With NONMEM, they are considered
as constants over individuals. The
’s. With a
population model these variances could change from
individual to individual. With NONMEM, they are considered
as constants over individuals. The
 ’s can co-vary. A
covariance matrix
’s can co-vary. A
covariance matrix  , like
the
, like
the  matrix given in
Section 4.1, gives the variances and covariances of the
matrix given in
Section 4.1, gives the variances and covariances of the
 ’s, as already
discussed at the end of Chapter 3. This does not preclude
the magnitudes of the errors from being affected by fixed
effects. A model such as (3.8) can still be used. This is
shown explicitly by the general model given in the next
section.
’s, as already
discussed at the end of Chapter 3. This does not preclude
the magnitudes of the errors from being affected by fixed
effects. A model such as (3.8) can still be used. This is
shown explicitly by the general model given in the next
section.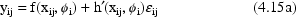

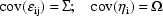
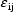 ,
,
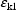 independent for
independent for
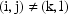
 ,
,
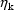 independent for
independent for
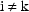
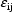 ,
,
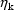 independent for all
independent for all
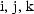 ,
,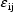 is a
vector, along with
is a
vector, along with 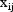 ,
,
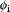 ,
,
 and
and
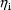 , and
, and
 and
and
 are square matrices with
dimensions equal to those of
are square matrices with
dimensions equal to those of
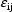 and
and
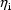 .
.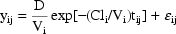

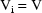
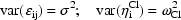
 are all
equal to a constant
are all
equal to a constant 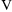 , i.e.
there is no random interindividual variability in the volume
of distribution, so that for the sake of this example,
, i.e.
there is no random interindividual variability in the volume
of distribution, so that for the sake of this example,
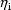 is just a scalar.
is just a scalar.