
NONMEM Users Guide Part V - Introductory Guide - Chapter 7
Chapter 7 - $SUBROUTINE Record and $PK Record
This chapter tells how to write a $SUBROUTINE record and how to write a simple $PK record for both individual and population data. This chapter is meant to be read in parallel with Chapters 3 and 4.
The $SUBROUTINE record describes which pharmacokinetic model is to be used. Recall that NONMEM calls a subroutine named PRED to compute the predicted value. The user must choose to use his own PRED subroutine or to use the PREDPP package. In this text it is assumed that the PREDPP package is chosen.
The PREDPP Library includes five subroutines
which are pre-preprogrammed, each for a specific
pharmacokinetic model. They are:
ADVAN1 (One Compartment Linear Model)
ADVAN2 (One Compartment Linear Model with First Order
Absorption)
ADVAN3 (Two Compartment Linear Model)
ADVAN4 (Two Compartment Linear Model with First Order
Absorption)
ADVAN10 (One Compartment Model with Michaelis-Menten
Elimination)
PREDPP calls only one subroutine, ADVAN; the different names
above are external names distinguishing different instances
of the ADVAN routine in the PREDPP Library. The name
’ADVAN’ is used because the routine advances
(i.e. updates the state of) the kinetic system from one
point in time to the next. There are additional ADVAN
routines in the Library which implement more general types
of pharmacokinetic models; see Chapter 12, Section 2.2. Each
of the ADVAN’s can be used for either individual or
population data. The (external) name of the ADVAN to be used
is coded on the $SUBROUTINE record; this also implies that
PREDPP is to be used.
----------

As an example, the following record specifies the
One Compartment Linear Model:
$SUBROUTINE ADVAN1
The five ADVAN’s are described in Appendix 1. They share certain features.
|
1. |
The compartments are numbered. These numbers are used in two places. First, they are used in the CMT and PCMT data items to describe specific compartments. Second, the compartment number n is part of the name of PK parameters such as compartment scale (Sn), as discussed below. |
|
2. |
Each model has a default observation compartment, which for each of the five ADVAN’s happens to be the central compartment. If an event record contains an observation (i.e. is an observation event record), the prediction associated with that record will be the scaled drug amount in this compartment, unless the CMT data item on the record specifies differently. The prediction associated with a non-observational event record will again be the scaled drug amount in this compartment, unless the PCMT data item on the record specifies differently. |
|
3. |
Each model has a default dose compartment. Unless specified differently by the CMT data item, it is understood that a dose is input into this compartment. With ADVAN1, ADVAN3, and ADVAN10, this is the central compartment. With ADVAN2 and ADVAN4, a drug depot compartment is part of the model and is the default dose compartment. In these cases, if a dose is to go directly into the central compartment, its compartment number (2) must be present in the CMT data item of the dose record. Note that it is never required that there be doses into the depot compartment. In a study involving mixed oral and IV doses, for example, some patients may receive only IV doses. All dose event records for such patients will have the value 2 in the CMT data item. |
|
4. |
Each model has an output compartment. The amount of drug in this compartment is the accumulated amount of drug eliminated from the system and typically represents the amount of drug which accumulates in the urine. This compartment is special. It may not receive a dose. It is initially off, and it remains off (so that the amount therein remains zero) until it is explicitly turned on by an other type event record which has the output compartment’s number in the CMT data item. It is computed by "mass balance", as follows. Between any two points in time, it increases by an amount equal to the amount of drug in the other compartments at the first point in time, plus the amount added via doses between the two time points, less the amount remaining in the other compartments at the second point in time. (This difference is multiplied by an output fraction (F0) parameter, if F0 is computed by the PK routine.) The output compartment can be turned off (i.e. its amount reset to zero). If the compartment is interpreted as a urine compartment, this is equivalent to "emptying" the compartment. This is done by putting the negative of its number in the CMT data item of an other type or observation event record. |
On event records, the output compartment is referred to by the compartment number given in Appendix 1. A PK parameter which refers to the output compartment may use either this number or 0 (zero). Thus, F0 and F2 both denote the output fraction for ADVAN1; similarly, S0 and S4 both denote the scale for ADVAN4’s output compartment.
|
5. |
Each model has a set of basic (required) pharmacokinetic (PK) parameters, which are the microconstants used to compute the amounts of drug via the kinetic equations for the model. Each one also has a set of additional (optional) PK parameters, including compartment scales (Sn), bioavailability fractions (Fn), and output fraction (F0). Compartment scales are typically used to convert amounts to concentrations, but they also can be used for other purposes. Bioavailability fractions multiply dose amounts. The output fraction is described above. |
|
6. |
Each model’s basic and additional pharmacokinetic parameters must be computed for it by a subroutine named PK. The error model must be described by a subroutine named ERROR. $PK and $ERROR abbreviated code provide an easy way to specify the essential computations that must occur in these subroutines. |
As discussed in Chapter 3, we may prefer to use pharmacokinetic parameters in our PK routine other than the microconstants used by PREDPP. Appendix 2 shows several commonly-used parameterizations. The PREDPP package includes a family of subroutines called TRANS routines which are pre-programmed to translate (reparameterize) from these commonly used parameterizations to the ones expected by PREDPP. Appendix 2 also gives the TRANS routine for each alternative parameterization. As with ADVAN, TRANS is the name of the routine. The names given in Appendix 2 are instances of external subroutine names used in the PREDPP Library. The first member of the family, TRANS1, simply translates a set of microconstants into these same microconstants and must be included in the NONMEM load module in lieu of the others when the $PK abbreviated code computes the microconstants.
The user must describe on the $SUBROUTINE record
which TRANS routine is to be used. For example, the
following record requests the One Compartment Linear Model
parameterized (in the PK routine) in terms of clearance and
volume.
$SUBROUTINE ADVAN1,TRANS2
When a TRANS other than TRANS1 is used, only the alternative
parameters listed in column 1 need be assigned values in the
$PK abbreviated code. In this example, these are CL, V, and
KA.
Note that TRANS1 is the default. That is, if no TRANS routine is listed on the $SUBROUTINE record, it is assumed that TRANS1 is intended. This is the case in the examples of Chapter 2. Alternative parameterizations using TRANS1 are discussed later in this chapter in Section 4.2.
The $SUBROUTINE record also describes how the
abbreviated code is to be implemented, as discussed in
Section 3 of Chapter 1. The choices are: DOUBLE
(double-precision FORTRAN subroutines), SINGLE
(single-precision FORTRAN subroutines), or LIBRARY (library
subroutines whose precision is chosen at the time the
NONMEM-PREDPP load module is built). The default is DOUBLE.
Thus, the following two records are equivalent:
$SUBROUTINE ADVAN1,TRANS2
$SUBROUTINE ADVAN1,TRANS2 DOUBLE
$PK abbreviated code consists of a block of $PK statements, one per line, which look much like FORTRAN77 statements. In fact, they are a subset of FORTRAN77: simple assignment statements and certain kinds of conditional (IF) statements. The $PK abbreviated code must be preceded by a record containing the characters "$PK". This record and the abbreviated code constitute the $PK record.
$PK statements must include assignment statements giving a value to every basic PK parameter for the given ADVAN and TRANS combination, as listed in Appendix 1 (when TRANS1 is used) or column 1 of Appendix 2 (when a different TRANS is used). They may also include assignment statements giving values to one or more of the additional PK parameters.
We assume the readers of this document are familiar with writing FORTRAN assignment and conditional statements. If not, the examples in this and the following chapter should give adequate guidance. FORTRAN statement numbers are not used, and the statements may start in any column. As with all NM-TRAN records, blank lines are permitted, and all text following a semi-colon (;) is ignored and may be used for comments. FORTRAN continuation lines are not permitted.
The statements are built using the following: elements of the THETA array (e.g., THETA(1)); constants; names of input data items appearing on the $INPUT record; names of previously-assigned variables; FORTRAN library functions SQRT, LOG, LOG10, and EXP; arithmetic operators +, -, *, /, **; and arithmetical and logical expressions using all of the above. In addition, statements may include representations for random variables such as ETA(1) and EPS(3). Input data items have the values appearing on the current event record, and thus these values may change from one event record to the next. A user-defined variable name follows the usual FORTRAN rules (1-6 letters and digits, starting with a letter) and may not be subscripted. It is defined ("declared") by being assigned a value (i.e., by appearing to the left of = in an assignment statment).
Neither nested parentheses nor nested IF statements are allowed, but this restriction can be avoided by the use of user-defined variables. Moreover, a pair of parentheses enclosing a subscript may be nested within another pair of parentheses. All subscripts must be constants (e.g. THETA(1)). The statements are evaluated sequentially, in the order in which they appear.
All variables, constants, and expressions are evaluated using floating-point (not integer) arithmetic. Single or double precision function names and constants may be used interchangeably. The choice of single precision versus double precision is made on the $SUBROUTINES record and overrides the apparent precision of the statements.
$PK statements are normally evaluated with every
event record for both population and individual
data†. This enables the amounts in the compartments
to be updated from event time to event time using current
values of the data items.
----------

This may be more frequent than is necessary. In the theophylline example of Chapter 2, no data item is used in the $PK statements. In the phenobarbital example, the data item used, WT, is constant within any individual’s data. In these cases, it is sufficient, and it can save noticeable amounts of run time, to evaluate the $PK statements once per individual record. PREDPP can be instructed that the set of event records with which the $PK statements are evaluated are to be limited in some way (see Chapter 12, Section 2.6). The CALL data item can be used to force the statements to be evaluated with any event records.
Certain advanced forms of dosing (additional and lagged doses; see Chapter 12, Sections 2.4 and 2.5) introduce doses at times which do not necessarily coincide with any event record. PREDPP does not normally evaluate the $PK statements at such times, but can be instructed to do so (Chapter 12, Section 2.6).
The state of the kinetic system at a given event time is obtained using PK parameter values computed with the data items on the event record. Using these parameter values the system is advanced to the event time from the last event time. Population models sometimes use data items which change value within individual records and thus give
rise to PK parameters whose values change within individual records. In Chapter 4, Section 3.1.6, it is pointed out that it is desirable for the value of such a data item on the event record to be that value holding at the midpoint of the interval between the current event time and the last previous event time, since the system is advanced over this interval using the PK parameters determined with this value.
If the data item changes too rapidly for this
value to fairly represent the data item over the entire time
period, it is possible to subdivide the interval into
smaller intervals. Event records with EVID=2 (other type
event records) can be introduced for this purpose. For
example, between two consecutive event records
 and
and
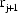 , with event times
, with event times
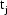 and
and
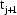 , one might introduce two
new other type event records
, one might introduce two
new other type event records  and
and 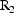 , with event times
, with event times
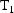 and
and
 , into the data set. The
value of the data item in
, into the data set. The
value of the data item in  will be used to compute the PK parameters used to advance
the system over the interval
will be used to compute the PK parameters used to advance
the system over the interval
 to
to
 and should be the value of
the data item holding at the midpoint of this interval.
Similarly, the value of the data item in
and should be the value of
the data item holding at the midpoint of this interval.
Similarly, the value of the data item in
 will be used to compute the
PK parameters used to advance the system over the interval
will be used to compute the
PK parameters used to advance the system over the interval
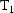 to
to
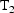 and should be the value of
the data item holding at the midpoint of this interval, and
so on.
and should be the value of
the data item holding at the midpoint of this interval, and
so on.
With individual data, the parameters to be
estimated are (usually) the individual’s PK
parameters, and therefore, elements of
 should be associated with
these PK parameters. (NONMEM estimates the elements of the
should be associated with
these PK parameters. (NONMEM estimates the elements of the
 vector.) By an
individual’s PK parameters, we mean here the basic PK
parameters and, possibly, some additional PK parameters
(e.g. a bioavailability fraction, or volume of distribution
when the latter is not a basic PK parameter). To illustrate,
in the theophylline example of Chapter 1 there occur these
$PK statements
vector.) By an
individual’s PK parameters, we mean here the basic PK
parameters and, possibly, some additional PK parameters
(e.g. a bioavailability fraction, or volume of distribution
when the latter is not a basic PK parameter). To illustrate,
in the theophylline example of Chapter 1 there occur these
$PK statements
$PK
KA=THETA(1)
K=THETA(2)
The parameters KA and K are the basic PK parameters for
ADVAN2 and TRANS1 (the default TRANS routine). They are used
to compute the amounts in the compartments. Typically,
however, the observations are concentrations. A scale
parameter is used to convert the amount into a
concentration. Thus, in the theophylline example we see two
additional $PK statements:
V=THETA(3)
S2=V
Here, V is a user-defined variable standing for the volume
of distribution of the central compartment. It is neither a
basic nor additional parameter. The parameter S2 is the
scale parameter for the central compartment; upon dividing
the amount in that compartment by S2, the concentration
results. (An observation is usually predicted by an amount
for a compartment divided by that compartment’s scale
parameter). In fact, these two statements could be replaced
by the single statement
S2=THETA(3)
However, it may be helpful to the user to distinguish in his
code between the calculation of the central volume itself
and the calculation of the scale parameter.
There is no particular need for certain elements
of  to be associated with
certain PK parameters. In the above example, the roles of
to be associated with
certain PK parameters. In the above example, the roles of
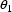 and
and
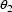 could have been reversed.
NONMEM’s
could have been reversed.
NONMEM’s  vector may
contain more or fewer elements than there are PK parameters,
depending on how these parameters are modeled.
vector may
contain more or fewer elements than there are PK parameters,
depending on how these parameters are modeled.
PK parameters must be explicitly modeled, usually
in terms of parameters to be estimated and user-defined data
items; the user communicates this model with the $PK
statements. If a certain parameter’s value is known
a priori (say, S2 has the known value 500), there are
several ways the value can be incorporated into the $PK
statements. The following examples show how it can be done
via a constant, via a fixed element of
 , and via a
(differently-named) data item:
, and via a
(differently-named) data item:
|
1. |
|
S2=500 |
|
2. |
|
$THETA .6 9. (500 FIXED) |
|
3. |
|
$INPUT ... VOL .. |
It is possible to use an alternative parameterization while still using TRANS1. The reparameterization is performed within the $PK statements by explicitly computing the microconstants from the alternative parameters. Such "reparameterization" statements are given in column 2 of Appendix 2. They must follow the assignment statements that give the alternative parameters their values, as in the phenobarbital example of Chapter 2.
The advantage of using $PK statements to reparameterize, rather than using a TRANS subroutine, is that the NONMEM-PREDPP load module will then always consist of the same set of subroutines for a given choice of ADVAN, which simplifies the job of creating and running it. It will also run slightly faster. We assume in this document that this approach is taken.
Other parameterizations are possible besides the
ones in Appendix 2. For example, with ADVAN1 and TRANS1, one
might code:
CL=THETA(1)
K=THETA(2)
V=CL/K
S1=V
The ability to express a large variety of
modeling possibilities with NONMEM-PREDPP provides great
freedom and flexibility, but as always with flexible
modeling capability, certain pitfalls arise. Suppose, for
example, that with a one compartment system the compartment
amount, rather than the concentration is observed. With
ADVAN1 and TRANS1 the statements
CL=THETA(1)
V=THETA(2)
K=CL/V
will lead to difficulty because only the ratio of
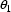 to
to
 affects the amount in the
compartment, and therefore, the data do not allow
affects the amount in the
compartment, and therefore, the data do not allow
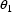 and
and
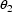 to be separately estimated.
The statements should read:
to be separately estimated.
The statements should read:
K=THETA(1)
It is important to remember that only those
elements of  which affect
the predictions of observations will be estimated by NONMEM.
Here is some problematic code using ADVAN1 with
TRANS1:
which affect
the predictions of observations will be estimated by NONMEM.
Here is some problematic code using ADVAN1 with
TRANS1:
K=THETA(1)
V=THETA(2)
CL=THETA(3)
S1=V
Once again, NONMEM will be unable to produce separate
estimates of all elements of
 . The kinetics of a simple
one compartment system cannot be determined by three
independent parameters. With TRANS1, PREDPP itself does not
"know" about the relationship K=CL/V which defines
a dependency among the parameters. Indeed, the parameters CL
and V are both regarded as user-defined variables. The value
of
. The kinetics of a simple
one compartment system cannot be determined by three
independent parameters. With TRANS1, PREDPP itself does not
"know" about the relationship K=CL/V which defines
a dependency among the parameters. Indeed, the parameters CL
and V are both regarded as user-defined variables. The value
of  has no effect on the
prediction. Were it not for the fact that S1 is set equal to
V, the value of
has no effect on the
prediction. Were it not for the fact that S1 is set equal to
V, the value of 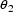 would have
no effect on the prediction either. With TRANS2 this code is
also incorrect for essentially the same reason. Here, K is
regarded as a user-defined variable, and the relationship
CL=K*V is not "known" to PREDPP. (PREDPP does know
that CL/V is the rate constant of elimination, but it does
not recognize the variable K as denoting this rate constant,
and
would have
no effect on the prediction either. With TRANS2 this code is
also incorrect for essentially the same reason. Here, K is
regarded as a user-defined variable, and the relationship
CL=K*V is not "known" to PREDPP. (PREDPP does know
that CL/V is the rate constant of elimination, but it does
not recognize the variable K as denoting this rate constant,
and  has no effect on the
prediction.)
has no effect on the
prediction.)
Scale parameters are mentioned in Section 2.1. Predicted compartment amounts are divided by them and are thus converted to predicted concentrations. They are only needed for those compartments whose concentrations are directly observed. With ADVAN3, for example, the peripheral compartment’s scale S2 does need to be computed explicitly if there are no observation events giving measured values of concentrations in the peripheral compartment. Predicted values for this compartment may still be plotted against time, for example, but these values need not be scaled drug amounts; the (unscaled) amount alone is sufficient to show the shape of the curve. (The various volume parameters shown in Appendix 2 must be modeled when they are used as basic parameters, but they need not be assigned as values to compartment scale parameters.) Any scale parameter which is not modeled by $PK statements is assumed to be 1 (i.e., predicted values are always amounts).
In Chapter 3, Section 2.2.1, the units of V were changed from kiloliters to liters using the model:
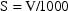
This can be coded in a $PK statement similar to
the way it appears here, except that the compartment number
must be specified:
S1=V/1000
Basic PK parameters may also be rescaled in this
manner.
In Chapter 3, Section 2.2.2, the following model appeared:

There are two ways this can be coded in $PK
statements. The 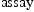 data item
can be tested directly, or an indicator variable can be
used. An indicator variable is a variable whose value is 0
or 1. It may be identified with an input data item, or it
may be a user-defined variable in the $PK statements. For
example, suppose variable ASY is to be used as an indicator
variable. If some input data item is given value 1 when
assay 1 was used and value 0 when assay 2 was used, then
this data item could simply be named ASY on the $INPUT
record. Suppose, however, that the assay number itself (1 or
2) was recorded in the data and that we have named the data
item ANUM on the $INPUT record. We must compute the
user-defined variable ASY for use as an indicator variable.
There are two ways this can be done: using a logical IF and
using a block IF.
data item
can be tested directly, or an indicator variable can be
used. An indicator variable is a variable whose value is 0
or 1. It may be identified with an input data item, or it
may be a user-defined variable in the $PK statements. For
example, suppose variable ASY is to be used as an indicator
variable. If some input data item is given value 1 when
assay 1 was used and value 0 when assay 2 was used, then
this data item could simply be named ASY on the $INPUT
record. Suppose, however, that the assay number itself (1 or
2) was recorded in the data and that we have named the data
item ANUM on the $INPUT record. We must compute the
user-defined variable ASY for use as an indicator variable.
There are two ways this can be done: using a logical IF and
using a block IF.
|
1. |
|
ASY=1 |
|
2. |
|
IF (ANUM.EQ.1) THEN |
The choice between these forms of IF is purely a
matter of style. Now let us assume that the compartment to
be scaled is compartment 2, and that
 is to be identified with
is to be identified with
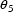 . The parameter S2 can now
be coded unconditionally:
. The parameter S2 can now
be coded unconditionally:
S2=ASY*V+(1-ASY)*THETA(5)*V
Alternatively, ANUM can be tested and ASY avoided altogether:
|
1. |
|
S2=V |
|
2. |
|
IF (ANUM.EQ.1) THEN |
If observations of urine concentration
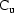 are included in the data
(see e.g. Chapter 6, Section 9), it is necessary to provide
urine volume as a scale for the output compartment.
Presumably, this volume varies between urine observations
and is recorded in the data records. Suppose this data item
is called UVOL in the $INPUT record. (The name given to the
data item has no special significance; any name could be
chosen.) An additional $PK statement is necessary:
are included in the data
(see e.g. Chapter 6, Section 9), it is necessary to provide
urine volume as a scale for the output compartment.
Presumably, this volume varies between urine observations
and is recorded in the data records. Suppose this data item
is called UVOL in the $INPUT record. (The name given to the
data item has no special significance; any name could be
chosen.) An additional $PK statement is necessary:
S0=UVOL
UVOL need be recorded on only those observation events to
which it applies, although it does no harm to record it on
other event records. For example, it may well happen that
both plasma and urine responses are measured at the same
time, so that there are two observation event records with
the same value of TIME, one for each compartment observed at
that time. As described in Section 3.2 above, $PK statements
are normally evaluated with every event record. Consider,
for example, the sample data below. Assume that the Central
compartment is compartment 2 and the output compartment is
compartment 3. (Note the use of -3 to signify that
compartment 3 is to be turned off after the observation
time. The compartment will remain off until the time another
urine collection begins, as indicated with an other type
record; see Chapter 6, Section 7.4). Either 1. or 2. will
produce the correct value of S0:
|
1. |
Record UVOL on the event record to which it applies. The order of the records does not matter. |
|
TIME UVOL DV CMT |
|
2. |
Record UVOL on all event records having the same value of TIME. The order of the records does not matter. |
|
TIME UVOL DV CMT |
The following will not produce the correct value
of S0 unless PREDPP is instructed to evaluate the $PK
statements only once for each distinct value of
TIME†:
----------

|
TIME UVOL DV CMT |
PK parameters of the form Fn, where n is the
number of a compartment into which a dose may be introduced,
are bioavailability fractions. If a dose record specifies a
dose for compartment n, the dose amount given on the event
record is multiplied by the value of Fn computed from the
$PK statements evaluated with this record, and this product
is the dose amount introduced into the system.‡ For
example, F1 multiplies the amount of dose which is to be
added to compartment 1. Any Fn which is not computed by $PK
statements is assumed to be 1 (i.e., the dose is 100%
available).
----------

As an example, suppose two different preparations
of the same drug are administered, and it is assumed that
they differ only in their bioavailability. The indicator
variable (or data item) PREP has value 1 for the first
preparation and 0 for the second. The ratio of the
bioavailability of the second preparation to that of the
first preparation is identified with
 . Usually, the method of
drug administration permits this ratio to be estimated, but
not the separate bioavailabilities. Without loss of
generality, the bioavailability of the first preparation can
be taken to be 1. Assuming the drug enters compartment 1 of
the model, there are three ways this can be
coded:
. Usually, the method of
drug administration permits this ratio to be estimated, but
not the separate bioavailabilities. Without loss of
generality, the bioavailability of the first preparation can
be taken to be 1. Assuming the drug enters compartment 1 of
the model, there are three ways this can be
coded:
|
1. |
|
F1=PREP+(1-PREP)*THETA(6) |
|
2. |
|
F1=1 |
|
3. |
|
IF (PREP.EQ.0) THEN |
Again, the choice is a matter of style.
Once a dose is introduced into the dose compartment, it begins to distribute into the other compartments. Whether or not the original dose was 100% available, it is assumed that none of the dose appearing in the dose compartment, and in other compartments after the dose is introduced, is further reduced due to bioavailability effects. PREDPP cannot model "bioavailability effects" between compartments.
The Output Fraction parameter, F0, is an optional
additional PK parameter of every model. As discussed in
Section 2 above, every model contains an output compartment.
If this compartment has been turned on prior to the advance
from time 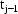 to time
to time
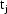 , then the amount of drug
lost from the system during this interval via elimination is
multiplied by F0 and added to the prior contents of the
output compartment. If the $PK statements do not include an
assignment statement giving a value to F0, it is taken to be
1 (i.e., 100% of the drug excreted goes to the output
compartment). In model (4.7), an example of the use of F0 is
given. Assuming that the variables CLREN (renal clearance)
and CL (total clearance) have been calculated with earlier
$PK statements, the statement
, then the amount of drug
lost from the system during this interval via elimination is
multiplied by F0 and added to the prior contents of the
output compartment. If the $PK statements do not include an
assignment statement giving a value to F0, it is taken to be
1 (i.e., 100% of the drug excreted goes to the output
compartment). In model (4.7), an example of the use of F0 is
given. Assuming that the variables CLREN (renal clearance)
and CL (total clearance) have been calculated with earlier
$PK statements, the statement
F0=CLREN/CL
can be used to compute F0.
With population data, the structural models for the PK parameters tend to be more complicated than with individual data. In addition, the influence of interindividual random effects needs to be described. These will involve differences in the $PK statements, but the same $SUBROUTINE record and the same ADVAN and TRANS subroutines are used, and the same general requirements and examples of the earlier sections of this chapter still mostly apply. In this section, the models of Chapter 4 are implemented via $PK statements. Many of these models could be implemented in a variety of ways; an experienced programmer may prefer to code them differently.
With population data, we must distinguish between
the typical value of a PK parameter in the population and
the value of that parameter for a given individual, the
individual’s value. The typical value is computed by a
structural model involving only fixed effects. We have
chosen to denote it with the use of a tilde: e.g.
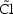 . The individual’s
value is computed by a model including random
interindividual effects (represented by random variables)
and is denoted without a tilde: e.g.,
. The individual’s
value is computed by a model including random
interindividual effects (represented by random variables)
and is denoted without a tilde: e.g.,
 . There is no tilde
character in the FORTRAN character set, and with NM-TRAN we
do not need to distinguish typical and individual values.
However, for purposes of clarity, in all the examples which
follow we will include the letters TV (Typical Value) at the
start of those variable names which we think of as having a
tilde (e.g., TVCL). This is a matter of style.
. There is no tilde
character in the FORTRAN character set, and with NM-TRAN we
do not need to distinguish typical and individual values.
However, for purposes of clarity, in all the examples which
follow we will include the letters TV (Typical Value) at the
start of those variable names which we think of as having a
tilde (e.g., TVCL). This is a matter of style.
In models such as (4.3), the subscript
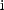 indicates that the model
applies to the
indicates that the model
applies to the 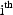 individual.
As noted in Chapter 4, the subscript is not needed and,
indeed, is not used in $PK statements.
individual.
As noted in Chapter 4, the subscript is not needed and,
indeed, is not used in $PK statements.
Models (4.4), (4.5a), (4.5b) and (4.6) can be
coded as they appear. Assuming that WT, AGE, and SECR are
input data items or have been calculated with earlier $PK
statements, the code is:
TVCLM=THETA(1)*WT
RF=WT*(1.66-.011*AGE)/SECR
TVCLR=THETA(4)*RF
TVCL=TVCLM+TVCLR
Model (4.4.1) can be coded as follows:
TVLCLM=THETA(1)+THETA(2)*LOG(WT)
TVCLM=EXP(TVLCLM)
Model (4.4.2) can also be coded as it
appears:
TVCLM=THETA(1)*WT**THETA(2)
Model (4.4.3) presents two problems. First,
subscripted variables that can appear in $PK statements are
few; naturally, they include THETA and (as seen below) ETA.
The variable CPSS cannot be subscripted, and a variable name
such as CPSS2 (rather than CPSS(2)) must be used for
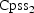 . Second, nested
parentheses cannot be used except when an inner set of
parentheses is used to enclose a subscript or an argument to
a FORTRAN function. Model 4.4.3 cannot be coded exactly as
it appears because nested parentheses would be required. One
might choose to introduce an intermediate variable,
signifying the reduction in clearance:
. Second, nested
parentheses cannot be used except when an inner set of
parentheses is used to enclose a subscript or an argument to
a FORTRAN function. Model 4.4.3 cannot be coded exactly as
it appears because nested parentheses would be required. One
might choose to introduce an intermediate variable,
signifying the reduction in clearance:
RED=THETA(2)*CPSS2/(THETA(3)+CPSS2)
TVCLM=WT*(THETA(1)-RED)
Of course, in this particular case it is easy to rewrite
4.4.3 and eliminate the need for the outer
parentheses.
TVCLM=WT*THETA(1)-WT*THETA(2)*CPSS2/(THETA(3)+CPSS2)
When dealing with typical values, indicator variables (0/1 variables) can be used interchangeably with conditional (IF) statements, as we have already seen. Model (4.4.4) can be coded in a variety of ways, two of which are:
|
1. |
|
TVCLM=(THETA(1)-THETA(2)*HF)*WT |
|
2. |
|
IF (HF.EQ.0) THEN |
Random variables  are used in the models for interindividual errors. (With
population models, random variables
are used in the models for interindividual errors. (With
population models, random variables
 are used in the models for
intraindividual errors; see Chapter 4, Section 2.) In $PK
statements they are denoted by ETA(1), ETA(2), etc. Even if
there is only once such variable it must still be
subscripted. It is the presence of one or more such
variables that indicates to NM-TRAN that the data is from a
population. Just as there is no particular need for certain
are used in the models for
intraindividual errors; see Chapter 4, Section 2.) In $PK
statements they are denoted by ETA(1), ETA(2), etc. Even if
there is only once such variable it must still be
subscripted. It is the presence of one or more such
variables that indicates to NM-TRAN that the data is from a
population. Just as there is no particular need for certain
 elements to be identified
with certain PK parameters, there is no particular need for
certain
elements to be identified
with certain PK parameters, there is no particular need for
certain  elements to be
associated with certain
elements to be
associated with certain 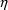 variables, and any association need not be one-to-one. The
following models are both valid:
variables, and any association need not be one-to-one. The
following models are both valid:
|
1. |
|
CL=THETA(1)+ETA(1) |
|
2. |
|
CL=THETA(1)+ETA(2) |
However, it will be easier to keep things straight if the first model is used.
Here are three different ways of coding a model for an individual’s value of clearance:
|
1. |
|
TVCL=THETA(1) |
|
2. |
|
CL=THETA(1) |
|
3. |
|
CL=THETA(1)+ETA(1) |
We prefer the first way because it clearly
distinguishes the model for the typical value from the model
for the individual’s value. With any of the three ways
for coding the model the typical value of the parameter can
be computed as follows: The 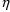 variables are set to 0, and the parameter is computed. Any
variable whose value depends on
variables are set to 0, and the parameter is computed. Any
variable whose value depends on
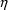 variables is called a
true-value variable because, in principle, it can
assume an individual’s true value under the model.
Such a variable is in contrast to a variable which assumes
only a typical value for the population.
variables is called a
true-value variable because, in principle, it can
assume an individual’s true value under the model.
Such a variable is in contrast to a variable which assumes
only a typical value for the population.
An individual’s true value is never actually known, although an estimate of it can be obtained. See Chapter 12, Sections 4.11-4.13.
Here we show how to express the most commonly used models for interindividual errors with $PK statements. In addition, all the error models described in Chapter 8 may also be used in $PK statements.
This is the error model of (4.9):
K=TVK+ETA(1)
This is the error model of (4.10):
K=TVK*(1+ETA(1))
This model can also be coded as:
K=TVK+TVK*ETA(1)
Here, the variable TVK has been "multiplied
through". The choice is a matter of style.
The model (4.11) may be coded as written:
CLM=TVCLM+(1-ICU)*ETA(1)+ICU*ETA(2)
Note that, under the parameterizations given in Appendices 1
and 2, CLM is neither a basic nor an additional PK
parameter, yet its model involves an
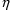 variable. This is
legitimate: any variable can be defined in terms of an
variable. This is
legitimate: any variable can be defined in terms of an
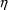 variable. However, just as
with
variable. However, just as
with  ’s, the values
assigned to the
’s, the values
assigned to the 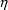 variables
must somehow affect the predictions of observations.
Otherwise, the variance of some
variables
must somehow affect the predictions of observations.
Otherwise, the variance of some
 variable cannot be
estimated, and consequently, none of the variances of these
variables can be estimated. Presumably, within the $PK
statements, CLM is used to compute CL, and (either within
the $PK statements or within the TRANS routine) CL is used
to compute K.
variable cannot be
estimated, and consequently, none of the variances of these
variables can be estimated. Presumably, within the $PK
statements, CLM is used to compute CL, and (either within
the $PK statements or within the TRANS routine) CL is used
to compute K.
This section discusses the use of true-value variables in some depth and may be skipped by the casual reader. The remarks here apply to all true-value variables: both the ETA variables of this chapter and the ERR/EPS variables of Chapter 8.
In general, ETA variables can be used like any other variables.
Any variable whose value is affected by an ETA
variable is a true-value variable, whether the ETA variable
occurs explicitly in the defining expression for the
true-value variable or whether another true-value variable
occurs in this expression. For example, consider the
following:
TVCLM=THETA(2)*WT
CLM=TVCLM+ETA(2)
RF=WT*(1.66-.011*AGE)/SECR
TVCLR=THETA(4)*RF
CLR=TVCLR+ETA(1)
CL=CLM+CLR
CL is a true-value variable, because it is computed from
true-value variables. It depends on both
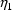 and
and
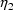 .
.
A true-value variable may not be changed. That is, it may not be assigned a different value by appearing on the left-hand side of a later $PK statement.
A variable may not appear on the right-hand side
of an assignment statement which redefines that same
variable to be a true-value variable. The only exception is
the simple additive model†:
CL=CL+ETA(1)
----------

A true-value variable may not be defined by or
used in conditional assignment statements. (Its value may be
tested in a logical expression, however.) Indicator (0/1)
variables are required when a variable is defined
conditionally in terms of true-value variables. For example,
model (4.11) could not be coded:
IF (ICU.EQ.0) THEN
CLM=TVCLM+ETA(1)
ELSE
CLM=TVCLM+ETA(2)
ENDIF
The only way this can be coded is unconditionally, using an
indicator variable:
CLM=TVCLM+(1-ICU)*ETA(1)+ICU*ETA(2)