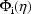 be
be
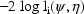 , and let
, and let
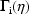 and
and
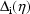 be the gradient (column)
vector and hessian matrix, respectively, of
be the gradient (column)
vector and hessian matrix, respectively, of
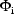 evaluated at
evaluated at
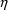 . An approximation to
. An approximation to
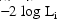 is given by
is given byLet 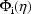 be
be
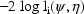 , and let
, and let
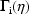 and
and
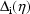 be the gradient (column)
vector and hessian matrix, respectively, of
be the gradient (column)
vector and hessian matrix, respectively, of
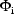 evaluated at
evaluated at
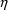 . An approximation to
. An approximation to
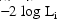 is given by
is given by
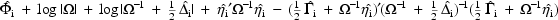
where 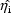 is some estimate
of
is some estimate
of 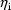 , and
, and
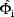 ,
,
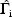 , and
, and
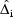 are
are
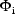 ,
,
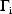 , and
, and
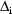 all evaluated at
all evaluated at
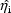 . This results from
applying a general approximation approach to integrals,
attributable to the French mathematician Laplace, and
described by De Bruijn (1961). With
. This results from
applying a general approximation approach to integrals,
attributable to the French mathematician Laplace, and
described by De Bruijn (1961). With
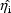 equal to the conditional
estimate obtained by maximizing the posterior density of
equal to the conditional
estimate obtained by maximizing the posterior density of
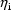 (in an unconstrained
manner) - call this the unconstrained conditional
estimate this particular approximation has been used by
others (Lindley, (1980); Mosteller and Wallace (1964)),
although not with a function
(in an unconstrained
manner) - call this the unconstrained conditional
estimate this particular approximation has been used by
others (Lindley, (1980); Mosteller and Wallace (1964)),
although not with a function
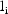 that is as complicated as
that which often arises in population pharmacokinetic and
pharmacodynamic analyses. See also: Tierny and Kadane
(1986). In this particular case, the last term of the
approximation is 0. In general, the approximation can
produce reasonable results as long the posterior
distribution of
that is as complicated as
that which often arises in population pharmacokinetic and
pharmacodynamic analyses. See also: Tierny and Kadane
(1986). In this particular case, the last term of the
approximation is 0. In general, the approximation can
produce reasonable results as long the posterior
distribution of 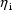 is
dominated by a single mode. On occasion, a randomly
dispersed parameter seems to have a multimodal distribution.
See the discussion in section B concerning mixture models
for a way to address this issue.
is
dominated by a single mode. On occasion, a randomly
dispersed parameter seems to have a multimodal distribution.
See the discussion in section B concerning mixture models
for a way to address this issue.
Each of the estimation methods uses a different variant
of this approximation. However, with whatever variant is
used, when in particular, the
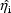 are taken to be conditional
estimates of the
are taken to be conditional
estimates of the 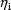 at
at
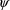 and
and
 , the general method
described in chapter I becomes what we call a conditional
estimation method. When the approximation is used just
as it is stated above, and when the
, the general method
described in chapter I becomes what we call a conditional
estimation method. When the approximation is used just
as it is stated above, and when the
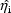 are taken to be the
unconstrained conditional estimates, the method is called
the Laplacian estimation method to honor the
individual whose approximation plays such an essential role.
However, the method itself involves an idea which is
peculiar to NONMEM implementation. Namely, the approximation
to L (the likelihood function of
are taken to be the
unconstrained conditional estimates, the method is called
the Laplacian estimation method to honor the
individual whose approximation plays such an essential role.
However, the method itself involves an idea which is
peculiar to NONMEM implementation. Namely, the approximation
to L (the likelihood function of
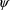 and
and
 ), resulting from using the
Laplacian approximation, is maximized.
), resulting from using the
Laplacian approximation, is maximized.
When mean-variance models are used, the assumption can
be made that each intraindividual variance-covariance matrix
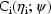 is actually given by
is actually given by
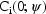 , the matrix for the mean
individual. With this particular assumption, there is said
to be no
, the matrix for the mean
individual. With this particular assumption, there is said
to be no 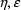 -interaction see chapter I. The
-interaction see chapter I. The
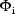 are computed differently,
depending on whether an
are computed differently,
depending on whether an 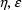 -interaction is assumed, as are the posterior modes. With
mean-variance models, by default, NONMEM implements the
Laplacian method assuming that there is no
-interaction is assumed, as are the posterior modes. With
mean-variance models, by default, NONMEM implements the
Laplacian method assuming that there is no
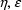 -interaction. With the
currently distributed NONMEM code it is possible to apply
the Laplacian method when there is an
-interaction. With the
currently distributed NONMEM code it is possible to apply
the Laplacian method when there is an
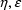 -interaction, but this code
and its usage are not supported by the NONMEM Project
Group.
-interaction, but this code
and its usage are not supported by the NONMEM Project
Group.
The matrix 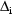 can be
approximated by another matrix. Suppose given
can be
approximated by another matrix. Suppose given
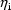 ,
,
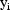 is comprised of
statistically independent subvectors
is comprised of
statistically independent subvectors
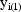 ,
,
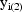 , etc., so that
, etc., so that
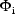 can be written as a sum
over terms
can be written as a sum
over terms 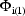 ,
,
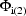 , etc. Then each of
, etc. Then each of
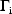 and
and
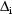 can be written as a sum
over terms
can be written as a sum
over terms 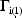 ,
,
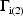 , etc. and
, etc. and
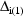 ,
,
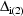 , etc., respectively. An
approximation
, etc., respectively. An
approximation 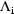 to
to
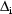 is obtained by replacing
each
is obtained by replacing
each 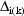 in the sum for
in the sum for
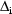 by
by
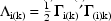 . This is a type of
first-order approximation; terms involving second
derivatives have been dropped. It is called the
first-order approximation
. This is a type of
first-order approximation; terms involving second
derivatives have been dropped. It is called the
first-order approximation
With this approximation, and when all the
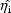 are taken to be equal to
the unconstrained conditional estimates of the
are taken to be equal to
the unconstrained conditional estimates of the
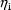 , the method is called the
first-order conditional estimation (FOCE) method
, the method is called the
first-order conditional estimation (FOCE) method
Actually, NONMEM allows the implementation of several versions of this method.
|
• |
When a mean-variance intraindividual model is used, by
default, |
|
• |
The first-order conditional estimation method without
interaction is the FOCE method applied with
intraindividual mean-variance models and assuming no
|
When the first-order approximation is used (with
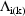 replaced by
replaced by
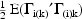 ), but when all
), but when all
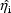 are taken to be 0 (the
population mean value of
are taken to be 0 (the
population mean value of 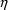 ),
the method is called the first-order (FO) estimation
method
),
the method is called the first-order (FO) estimation
method
With the first-order method, the terms
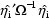 and
and
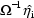 in the Laplacian
approximation are 0. Note that since conditional estimates
are not used, the first-order method is not a conditional
estimation method.
in the Laplacian
approximation are 0. Note that since conditional estimates
are not used, the first-order method is not a conditional
estimation method.
It can be shown that when intraindividual mean-variance models are used, the method is equivalent to the first-order method as described, for example, in NONMEM Users Guide - Part I (also see e.g., Beal and Sheiner (1985)). Such an earlier description is also given below in section A.6. These earlier descriptions of the method apply only to mean-variance models. With the currently distributed NONMEM code it is possible to apply the FO method as defined above with intraindividual models that are not mean- variance models, but this usage is not recommended, and the code is not supported by the NONMEM Project Group.
Suppose certain (but not all) elements of
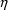 are chosen to be in a set
are chosen to be in a set
 , that the elements of
, that the elements of
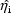 corresponding to the
elements of
corresponding to the
elements of  are taken to be
0, and that the remaining elements of
are taken to be
0, and that the remaining elements of
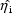 are taken to be those given
by the Bayes posterior mode of
are taken to be those given
by the Bayes posterior mode of
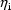 under the restriction
that all elements of
under the restriction
that all elements of 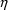 in
in
 are 0. The conditional
estimate thus defined is an example of a constrained
conditional estimate. Suppose also that the first-order
approximation is made. Then the method is a hybrid between
the first-order method and the FOCE method. Accordingly,
this conditional estimation method is called the hybrid
method Note that with the definition of the
are 0. The conditional
estimate thus defined is an example of a constrained
conditional estimate. Suppose also that the first-order
approximation is made. Then the method is a hybrid between
the first-order method and the FOCE method. Accordingly,
this conditional estimation method is called the hybrid
method Note that with the definition of the
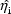 used with this method, in
contrast with the definition used with the FOCE and
Laplacian methods, the last term in the Laplacian
approximation is not 0.
used with this method, in
contrast with the definition used with the FOCE and
Laplacian methods, the last term in the Laplacian
approximation is not 0.
A hybrid method can be considered that uses a weaker
version of the first-order approximation. Consider using the
first-order approximation, but only for the submatrix of
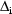 consisting of just those
partial second derivatives such that the two variables with
respect to which the differentiation occurs are in
consisting of just those
partial second derivatives such that the two variables with
respect to which the differentiation occurs are in
 . This method is not
supported with the currently distributed NONMEM code.
. This method is not
supported with the currently distributed NONMEM code.
When the intraindividual models are statistical linear
models (linear in the parameters
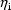 ), the first-order,
first-order conditional, hybrid, and Laplacian methods are
all the same method, the classical maximum likelihood
method.
), the first-order,
first-order conditional, hybrid, and Laplacian methods are
all the same method, the classical maximum likelihood
method.
The 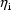 are assumed to be
distributed in the population with mean 0. When the
population model fits the data well, this will be
reflected by the average,
are assumed to be
distributed in the population with mean 0. When the
population model fits the data well, this will be
reflected by the average, 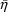 ,
of the conditional estimates of the
,
of the conditional estimates of the
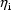 across the sampled
individuals (at the values of the population parameters
given by the model) being close to 0. (The converse does not
necessarily hold.) When
across the sampled
individuals (at the values of the population parameters
given by the model) being close to 0. (The converse does not
necessarily hold.) When 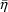 is
close to 0, the fit will be called centered There is
nothing about the methods defined above that insures that
the fit will be centered. There are infrequently arising
situations where the average is "far" from 0,
where the model does not fit well (as judged e.g. by the
differences
is
close to 0, the fit will be called centered There is
nothing about the methods defined above that insures that
the fit will be centered. There are infrequently arising
situations where the average is "far" from 0,
where the model does not fit well (as judged e.g. by the
differences 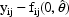 with
mean-variance intraindividual models) and where a method
that is designed to better center the fit might be tried
(do see chapter III for some guidance). With a
centering estimation method the
with
mean-variance intraindividual models) and where a method
that is designed to better center the fit might be tried
(do see chapter III for some guidance). With a
centering estimation method the
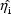 are taken to be the
unconstrained conditional estimates, and the approximation
to
are taken to be the
unconstrained conditional estimates, and the approximation
to 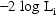 is given by
is given by
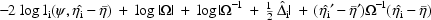
With NONMEM, there are centering FOCE and Laplacian
estimation methods (with no 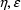 -interaction). A centering hybrid method is not implemented
in NONMEM.
-interaction). A centering hybrid method is not implemented
in NONMEM.
The first-order model is the population model
which results when for all i, the ith given intraindividual
model is a mean-variance model with mean
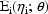 and variance-covariance
matrix
and variance-covariance
matrix 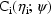 , and this model is
replaced by another such model with mean
, and this model is
replaced by another such model with mean
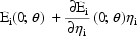
and variance-covariance matrix
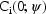 .
.
The linearity of the 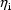 under this model implies that the population expectation of
under this model implies that the population expectation of
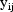 is
is
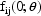 , the prediction obtained
by taking
, the prediction obtained
by taking 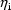 to be 0, its
population mean. With mean-variance models, the FO
estimation method is sometimes described as the application
of the maximum likelihood method to the first-order model
that results from the given model, and when using this
method, it is usual to judge goodness of fit by the
differences
to be 0, its
population mean. With mean-variance models, the FO
estimation method is sometimes described as the application
of the maximum likelihood method to the first-order model
that results from the given model, and when using this
method, it is usual to judge goodness of fit by the
differences 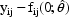 . When a
conditional estimation method is used instead of the FO
method, a centered fit may result, confirming that the
population mean of the
. When a
conditional estimation method is used instead of the FO
method, a centered fit may result, confirming that the
population mean of the 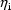 is
0. However, the given intraindividual models are used, and
they may be nonlinear in the
is
0. However, the given intraindividual models are used, and
they may be nonlinear in the
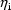 . Therefore, conceivably,
. Therefore, conceivably,
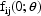 may be a poor
approximation to the population expectation of
may be a poor
approximation to the population expectation of
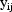 , and for this reason
alone, an apparent bias in the fit may result. Experience
suggests, though, that this should not be a major concern
(perhaps because the nonlinear effect is small relative to
the size of intraindividual variability in the residuals).
If one is concerned, there are a couple of strategies one
might use.
, and for this reason
alone, an apparent bias in the fit may result. Experience
suggests, though, that this should not be a major concern
(perhaps because the nonlinear effect is small relative to
the size of intraindividual variability in the residuals).
If one is concerned, there are a couple of strategies one
might use.
First, the NONMEM program allows the expectation of the
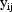 to be estimated by means
of a couple different types of actual integration (and not
just when the intraindividual models are of mean-variance
kind); see NONMEM Users Guide - Part VIII. Second, when the
intraindividual models are mean-variance models, NONMEM
allows the first-order model to be obtained automatically
from the given model and used with the centering FOCE
method. (If the first-order model is used with the
noncentering FOCE method, the result is the same as that
obtained with the FO method.) When a conditional estimation
method is needed (see chapter III), application of the
centering FOCE method to the first-order model that results
from the given model may yield adequate results, and of
course, the expectation of
to be estimated by means
of a couple different types of actual integration (and not
just when the intraindividual models are of mean-variance
kind); see NONMEM Users Guide - Part VIII. Second, when the
intraindividual models are mean-variance models, NONMEM
allows the first-order model to be obtained automatically
from the given model and used with the centering FOCE
method. (If the first-order model is used with the
noncentering FOCE method, the result is the same as that
obtained with the FO method.) When a conditional estimation
method is needed (see chapter III), application of the
centering FOCE method to the first-order model that results
from the given model may yield adequate results, and of
course, the expectation of 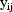 under the first-order model is simply given by
under the first-order model is simply given by
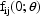 . Moreover, due to the
linearity of the intraindividual models (of the first-order
model) in the
. Moreover, due to the
linearity of the intraindividual models (of the first-order
model) in the 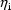 , the
computational requirement is substantially less than that
incurred with application of the (centering or noncentering)
FOCE method to the given model. The savings in CPU time is
achieved at the expense of possibly using too simple a model
(and, of course is still not as great a savings as is
achieved with the FO method).
, the
computational requirement is substantially less than that
incurred with application of the (centering or noncentering)
FOCE method to the given model. The savings in CPU time is
achieved at the expense of possibly using too simple a model
(and, of course is still not as great a savings as is
achieved with the FO method).
The first-order model may be used with the centering FOCE method, but not with the centering Laplacian method (because due to the linearity, the result would be the same as that obtained with the centering FOCE method). Be aware that when this model is used with the centering FOCE method, the conditional estimates produced by the method are based on the first-order intraindividual models (unlike whenever the noncentering FOCE method is used, where the conditional estimates are based on the given intraindividual models). It is possible nonetheless to obtain posthoc estimates based on the given intraindividual models, at the population estimates obtained from using the centering FOCE method with the first-order model. A centering hybrid method is not implemented in NONMEM.
On occasion, a model may need to incorporate a randomly
dispersed parameter that has a possibly multimodal
distribution. In this case a mixture model may be useful.
This is a model where for each i, there are several possible
intraindividual models, 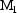 ,
,
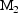 , ...,
, ...,
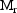 for
for
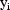 , and it is assumed that
the particular model that actually describes
, and it is assumed that
the particular model that actually describes
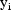 is one of these, but it is
not known which one. It is assumed that the probability that
it is
is one of these, but it is
not known which one. It is assumed that the probability that
it is 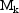 is
is
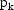 , where
, where
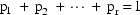 . Loosely put, the ith
individual is chosen randomly from a population divided into
. Loosely put, the ith
individual is chosen randomly from a population divided into
 subpopulations, their
relative sizes either being known or unknown. The
subpopulation of which the individual is a given member is
not observable, but for each subpopulation, a model for data
from an individual from the subpopulation is available. The
mixing probabilities
subpopulations, their
relative sizes either being known or unknown. The
subpopulation of which the individual is a given member is
not observable, but for each subpopulation, a model for data
from an individual from the subpopulation is available. The
mixing probabilities 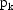 correspond to the sizes of the subpopulations and are
usually treated as parameters whose values are unknown and
are estimated. With NONMEM, these probabilities can be
modeled, i.e. related to covariables, and therefore, can
vary between individuals. The parameters of these
relationships can be estimated; they are included in
correspond to the sizes of the subpopulations and are
usually treated as parameters whose values are unknown and
are estimated. With NONMEM, these probabilities can be
modeled, i.e. related to covariables, and therefore, can
vary between individuals. The parameters of these
relationships can be estimated; they are included in
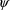 . To indicate this
generality, the
. To indicate this
generality, the 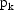 may be
written
may be
written 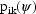 (the kth mixing
probability for the ith individual).
(the kth mixing
probability for the ith individual).
Suppose, for example, that a clearance parameter of a pharmacokinetic model may be bimodally distributed in the population. Here is how this may be expressed with a population model. One may consider a mixture model with two intraindividual models for each individual: for the ith individual, one where the individual’s clearance is given by

and another where it is given by

(The parameters 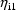 and
and
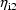 are the first two elements
of
are the first two elements
of 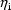 .) For each i, the
value
.) For each i, the
value 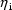 arises randomly (see
chapter I). For each i, a choice between the two
intraindividual models is also viewed as one being made in a
random fashion, according to probabilities
arises randomly (see
chapter I). For each i, a choice between the two
intraindividual models is also viewed as one being made in a
random fashion, according to probabilities
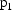 and
and
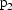 (
(
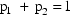 ). As a result of this
choice, a value
). As a result of this
choice, a value 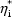 , which is
either
, which is
either 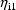 or
or
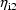 , is also
"chosen". (Consequently, if after
, is also
"chosen". (Consequently, if after
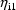 , say, is chosen, the
value of
, say, is chosen, the
value of 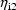 does not
influence the data.) From the point of view of not knowing
what choices between intraindividual models were actually
made, the distribution of the
does not
influence the data.) From the point of view of not knowing
what choices between intraindividual models were actually
made, the distribution of the
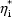 across individuals is a
mixture of two normal distributions, and the distribution of
the
across individuals is a
mixture of two normal distributions, and the distribution of
the 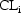 is a mixture of two
lognormal distributions.
is a mixture of two
lognormal distributions.
The first two elements of the random variable
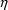 may have the same or
different variances, i.e.
may have the same or
different variances, i.e. 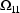 may or may not equal
may or may not equal 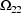 . If
these variances are sufficiently small, while the parameters
. If
these variances are sufficiently small, while the parameters
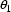 and
and
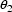 are sufficiently far
apart, and if both probabilities
are sufficiently far
apart, and if both probabilities
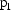 and
and
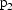 are sufficiently large
(however in this regard, the variances, the
are sufficiently large
(however in this regard, the variances, the
 ’s, and the
probabilities must actually be considered altogether), the
distribution of
’s, and the
probabilities must actually be considered altogether), the
distribution of 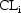 is
bimodal. Often, the data may not allow all of the different
variances between mixture components, such as
is
bimodal. Often, the data may not allow all of the different
variances between mixture components, such as
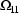 and
and
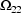 , to be well estimated, in
which case the assumption might be made that these variances
are the same (a homoscedastic assumption). With NONMEM, this
can be done explicitly, or alternatively, the "same
, to be well estimated, in
which case the assumption might be made that these variances
are the same (a homoscedastic assumption). With NONMEM, this
can be done explicitly, or alternatively, the "same
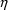 " can be used with
both mixture components, e.g.
" can be used with
both mixture components, e.g.
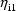 can be used in (3) and
also in (4), instead of
can be used in (3) and
also in (4), instead of 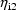 .
NONMEM will understand that
.
NONMEM will understand that
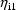 is symbolizing two
"different
is symbolizing two
"different 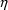 ’s", each having the same variance.†
’s", each having the same variance.†
----------
Other examples of mixture models may be given. See
NONMEM Users Guide - Part VI, section III.L.2 for an example
where the mixture model describes a mixture of two joint
lognormal distributions for clearance and volume, but
which is not a bimodal distribution. The differences
between the models 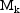 need
not be differences concerning parameters; they could be
differences in model form. They can be any set of
differences whatsoever.
need
not be differences concerning parameters; they could be
differences in model form. They can be any set of
differences whatsoever.
The likelihood for 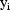 under a mixture model is
under a mixture model is
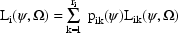
where 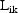 is the
likelihood function for
is the
likelihood function for 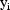 under the the kth possible intraindividual model for
individual i. With a mixture model, any of the estimation
methods described in section A uses the defining
approximation for the method with each of the
under the the kth possible intraindividual model for
individual i. With a mixture model, any of the estimation
methods described in section A uses the defining
approximation for the method with each of the
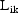 ,
,
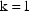 , ...,
, ...,
 .
.
With a set of values for the population parameters
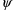 and
and
 , NONMEM classifies each
individual into one of the
, NONMEM classifies each
individual into one of the  subpopulations. The classification gives the most probable
subpopulation of which the individual is a member. For each
k, the empirical Bayes (marginal) posterior probability that
subpopulations. The classification gives the most probable
subpopulation of which the individual is a member. For each
k, the empirical Bayes (marginal) posterior probability that
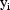 is described by
is described by
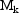 , given
, given
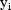 , is computed by
, is computed by
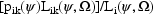 . The individual is
classified into the kth subpopulation if the kth probability
is the largest among these r values.
. The individual is
classified into the kth subpopulation if the kth probability
is the largest among these r values.
TOP
TABLE OF CONTENTS
NEXT CHAPTER ...