

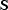 Depends on a Known Constant
Depends on a Known Constant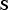 Depends on a Parameter
Depends on a Parameter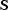 Depends on an Element of
Depends on an Element of 
NONMEM Users Guide Part V - Introductory Guide - Chapter 3
Chapter 3 - Models for Individual Data
In this chapter, the notation and definitions we will use to discuss models for individual data will be presented. The relationship of these models to data will be discussed, and a distinction between pharmacokinetic structural models (that describe the underlying shape and form of the data) and statistical error models (that describe the "errors" or differences between observations and structural model predictions) will be made. Several error models will be discussed, as will a useful modelling device, the indicator variable.
By individual data we usually mean data from a single individual (animal or human). One could also be concerned with data comprised of a pharmacokinetic response at just one time point from each of a number of individuals. Call this type of data single- response population data. This name comes from the fact that data such as these can, of course, be regarded as a particular instance of the more general data type, population data; i.e., data comprised of one or more pharmacokinetic responses at different time points from a number of individuals sampled from a population. Although one can discuss the treatment of single-response population data as population data, they are often treated just as are individual data.
A simple pharmacokinetic model for data from a single individual is the monoexponential ("one-compartment") model:

This model describes the typical time course of
amount of drug in the body ( 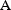 ), as a function of initial dose (
), as a function of initial dose (
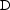 ), time (
), time (
 ), and a parameter,
), and a parameter,
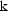 . As we may be interested in
. As we may be interested in
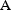 at several possible times,
we explicitly note this by the subscript
at several possible times,
we explicitly note this by the subscript
 which indexes a list of
times,
which indexes a list of
times, 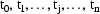 .
.
A way to write a generic form for a structural model, omitting details of its structure, is

where 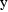 stands for
some "response" (dependent variable) of interest (
stands for
some "response" (dependent variable) of interest (
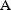 in (3.1)), the symbol
in (3.1)), the symbol
 stands for the unspecified
form of the model (a monoexponential such as in (3.1)),
which is a function of known quantities,
stands for the unspecified
form of the model (a monoexponential such as in (3.1)),
which is a function of known quantities,
 (
(
 and
and
 in (3.1)), and
parameters,
in (3.1)), and
parameters, 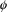 (
(
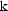 in (3.1)). The quantities
in x are known, because they are either measured or
controlled, and therefore, are called fixed effects,
in contrast to effects which are not known and are regarded
as random (see below). The parameters in the parameter
vector
in (3.1)). The quantities
in x are known, because they are either measured or
controlled, and therefore, are called fixed effects,
in contrast to effects which are not known and are regarded
as random (see below). The parameters in the parameter
vector 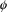 are called fixed
effect parameters because they quantify the influence of
the fixed effects on the dependent variable. Each one of an
individual’s pharmacokinetic parameters is a
particular type of fixed effect parameter. With NONMEM,
parameters comprising
are called fixed
effect parameters because they quantify the influence of
the fixed effects on the dependent variable. Each one of an
individual’s pharmacokinetic parameters is a
particular type of fixed effect parameter. With NONMEM,
parameters comprising  are
(usually) fixed effect parameters, but these may or may not
be an individual’s pharmacokinetic parameters
(contrast figures 2.1 and 2.6). Here we shall use the symbol
are
(usually) fixed effect parameters, but these may or may not
be an individual’s pharmacokinetic parameters
(contrast figures 2.1 and 2.6). Here we shall use the symbol
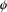 for the parameter vector
comprised specifically of an individual’s
pharmacokinetic parameters (although there will be some
exception to this).
for the parameter vector
comprised specifically of an individual’s
pharmacokinetic parameters (although there will be some
exception to this).
Aside from the fact that the values given by a
structural model are usually not the values observed due to
measurement error or model misspecification, an amount of
drug ( 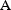 of (3.1)) is usually
not itself observable. Instead, we may observe a
concentration (
of (3.1)) is usually
not itself observable. Instead, we may observe a
concentration (  ) of drug.
We need an "observation scaling" model to describe
the relationship between
) of drug.
We need an "observation scaling" model to describe
the relationship between  and
and  . This might
be
. This might
be

where V is another parameter, Volume of
Distribution. (We denote the concentration in model (3.3) by
the symbol 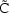 , to distinguish
it, the model-predicted value, from the actually observed
value,
, to distinguish
it, the model-predicted value, from the actually observed
value,  . This will soon be
discussed further.) PREDPP assumes that there is always an
observation scaling model like (3.3) that relates an amount
of drug (in some compartment of the body) to the
observation, and therefore always expects a parameter,
. This will soon be
discussed further.) PREDPP assumes that there is always an
observation scaling model like (3.3) that relates an amount
of drug (in some compartment of the body) to the
observation, and therefore always expects a parameter,
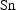 that scales (i.e. divides)
the predicted amount in the
that scales (i.e. divides)
the predicted amount in the 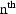 compartment. In the example above,
compartment. In the example above,
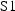 is simply
is simply
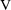 . In other examples, to be
discussed later,
. In other examples, to be
discussed later, 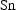 can be
more complicated. If a value for
can be
more complicated. If a value for
 is not specified, it is
taken to be 1. For the rest of this discussion, it is
convenient to assume that
is not specified, it is
taken to be 1. For the rest of this discussion, it is
convenient to assume that  itself includes a scaling parameter (if such is needed, and
even though such a parameter is not usually regarded as one
of an individual’s pharmacokinetic parameters) and
that
itself includes a scaling parameter (if such is needed, and
even though such a parameter is not usually regarded as one
of an individual’s pharmacokinetic parameters) and
that 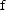 actually includes
observational scaling. Note, considering the example of
(3.3), that
actually includes
observational scaling. Note, considering the example of
(3.3), that 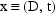 , and
, and
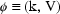 . Thus
. Thus
 and
and
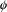 of (3.1) are in general
lists of things (vectors), not single things
(scalars).
of (3.1) are in general
lists of things (vectors), not single things
(scalars).
PREDPP implements a number of pharmacokinetic
models, such as the one-compartment model (3.1), (3.3).
These will be discussed more fully in Chapter 7. There is no
need for further general discussion of kinetic models, as we
assume the readers of this document are familiar with
pharmacokinetics. However, two modelling features deserve
further comment, alternative parameterizations and the
special parameter, 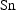 .
.
Recall the phenobarbital example of Chapter 2.
For the first run, the input contained, among other things,
some lines of code defining the variables
 and
and
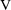 , and then the
line
, and then the
line
K = CL/V
This line was needed because PREDPP expects the
one-compartment model to be parameterized using the
parameter 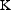 , the rate
constant of elimination, not clearance and volume of
distribution. However, we chose to estimate typical
population values for
, the rate
constant of elimination, not clearance and volume of
distribution. However, we chose to estimate typical
population values for  and
and
 , so we had to relate these
parameters to THETA and then relate
, so we had to relate these
parameters to THETA and then relate
 to
to
 and
and
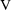 . This is an example of
reparametrization of a model so that the pharmacokinetic
parameters used are those of primary interest to the
modeler. In fact, we may use any parameterization we wish,
so long as we are willing to include the reparameterization
line(s) that translate our parameters into those expected by
PREDPP. (Chapter 7 discusses the parameters PREDPP expects
for the various models it implements.) However, there is a
program called TRANS which automatically does this
translation. Different versions of TRANS exist in the PREDPP
Library and correspond to translations of different
parameterizations into that expected by PREDPP.
. This is an example of
reparametrization of a model so that the pharmacokinetic
parameters used are those of primary interest to the
modeler. In fact, we may use any parameterization we wish,
so long as we are willing to include the reparameterization
line(s) that translate our parameters into those expected by
PREDPP. (Chapter 7 discusses the parameters PREDPP expects
for the various models it implements.) However, there is a
program called TRANS which automatically does this
translation. Different versions of TRANS exist in the PREDPP
Library and correspond to translations of different
parameterizations into that expected by PREDPP.

Usually, observations are concentrations. So, as
in model (3.3), 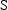 will
usually be set identical to
will
usually be set identical to 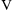 . However,
. However, 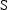 is not always
simply
is not always
simply 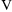 . Some examples
should clarify this point. (In the discussion below, we
avoid the notation
. Some examples
should clarify this point. (In the discussion below, we
avoid the notation 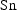 , and
use
, and
use 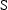 , to refer to the scale
term for the amount in the compartment in which
concentrations are being measured.)
, to refer to the scale
term for the amount in the compartment in which
concentrations are being measured.)
 Depends on a Known Constant
Depends on a Known ConstantThis almost trivial case occurs when one wishes
to match the units of predicted responses to those of the
data. For example, suppose 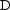 is in milligrams, but concentrations are in ng/ml. If no
scaling is done, the units of
is in milligrams, but concentrations are in ng/ml. If no
scaling is done, the units of
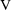 will be kiloliters (i.e.,
will be kiloliters (i.e.,
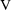 =1 corresponds to
=1 corresponds to
 =1000 liters). To avoid
this, one might choose the model
=1000 liters). To avoid
this, one might choose the model
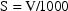
thereby converting the units of
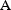 into micrograms, and since
mcg/L
into micrograms, and since
mcg/L  ng/ml, the units of
ng/ml, the units of
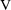 become liters. Of course,
one could recode one’s data, dividing all
concentrations by 1000 (or multiplying the dose by 1000) and
avoid this, but that may not be convenient.
become liters. Of course,
one could recode one’s data, dividing all
concentrations by 1000 (or multiplying the dose by 1000) and
avoid this, but that may not be convenient.
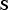 Depends on a Parameter
Depends on a ParameterLater in this chapter we will discuss a model used when the data arise from two different assays (call them assay 1 and assay 2). In such a case, there may be a systematic (multiplicative) bias of one assay relative to the other. If we wish to allow for this possibility, we might need a model such as

where  is a new
parameter that measures the proportional bias of the assays
(i.e., bias causes the apparent volume of distribution to be
different for data from the two assays). The parameter
is a new
parameter that measures the proportional bias of the assays
(i.e., bias causes the apparent volume of distribution to be
different for data from the two assays). The parameter
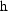 is not really a
pharmacokinetic parameter, but for the purpose of this
discussion it can be included in
is not really a
pharmacokinetic parameter, but for the purpose of this
discussion it can be included in
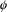 .
.
 Depends on an Element of
Depends on an Element of 
Later in this chapter we will describe a model
useful when two kinds of responses are measured, plasma and
urine concentrations. In the case of urine concentrations,
the predicted total drug in the urine during a time period
(available from an "output" compartment present in
all models implemented by PREDPP; see Chapter 7) would have
to be scaled by the actual urine volume during that time
period. This volume would be an element of
 , and
, and
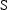 would be set equal to
it.
would be set equal to
it.
One does not, in fact, ever observe the predicted plasma concentration (or any other predicted response). What one observes is a measured value which differs from the predicted value by some (usually small) amount called a residual error (also called intra-individual error). We regard this error as a random quantity (see below). We will want NONMEM to fit our model to our data, and in so doing, provide us with estimates of the model parameters. The way NONMEM’s fit follows the data is determined largely by what we tell it about the nature of the errors (see Chapter 5). We must therefore provide NONMEM with another model, an error model.
There are many reasons that the actual
observation may not correspond to the predicted value (e.g.
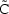 as given by the right side
of (3.3)) The structural model may only be approximate, or
the quantities in
as given by the right side
of (3.3)) The structural model may only be approximate, or
the quantities in  may have
been measured with error, or, as is always true,
pharmacokinetic responses may be measured with some error
(assay error). It is too difficult to model all these
sources of error separately, so we usually make the
simplifying assumption that each difference between an
observation and its prediction (i.e. each error) is a
randomly occurring number. When the data are from a single
individual, and the error model is the Additive error model
(see Section 3.1, below), the error is denoted by
may have
been measured with error, or, as is always true,
pharmacokinetic responses may be measured with some error
(assay error). It is too difficult to model all these
sources of error separately, so we usually make the
simplifying assumption that each difference between an
observation and its prediction (i.e. each error) is a
randomly occurring number. When the data are from a single
individual, and the error model is the Additive error model
(see Section 3.1, below), the error is denoted by
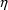 herein, by ETA in NONMEM
output, and by ETA or ERR in NM-TRAN input. (When data are
from a population, and the same error model is used, this
error will be denoted
herein, by ETA in NONMEM
output, and by ETA or ERR in NM-TRAN input. (When data are
from a population, and the same error model is used, this
error will be denoted  ; see
Chapter 4.) Therefore a model for the jth observation,
; see
Chapter 4.) Therefore a model for the jth observation,
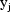 , could be
written
, could be
written

Implicit in using the symbol
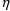 in this way is the
assumption that all residual errors come from probability
distributions with mean zero and the same (usually unknown)
variance. (The error variance is the mean squared
error.) More complicated error models involving
in this way is the
assumption that all residual errors come from probability
distributions with mean zero and the same (usually unknown)
variance. (The error variance is the mean squared
error.) More complicated error models involving
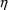 can be written (see below).
A schematic of model (3.4) is shown for the structural model
of (3.1), (3.3) in figure 3.1. Because this model describes
the influence of both fixed effects (
can be written (see below).
A schematic of model (3.4) is shown for the structural model
of (3.1), (3.3) in figure 3.1. Because this model describes
the influence of both fixed effects (
 ) and random effects
(
) and random effects
( 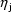 ), it is called a
Mixed Effects Model (hence the name, NONMEM:
NONlinear Mixed Effects Model).
Mixed effects models, in general, may have more than one
random effect, and more than one type of random effect
(Chapter 4); (3.4) is only a particularly simple
example.
), it is called a
Mixed Effects Model (hence the name, NONMEM:
NONlinear Mixed Effects Model).
Mixed effects models, in general, may have more than one
random effect, and more than one type of random effect
(Chapter 4); (3.4) is only a particularly simple
example.
Even though errors are unpredictable random
quantities, some information about them is usually assumed,
and some can be estimated. First, it is assumed that the
mean error is zero. This simply means that were the true
values for the parameters in
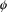 known, the model would have
no systematic overall bias (e.g., be systematically below or
above the data points, on average).
known, the model would have
no systematic overall bias (e.g., be systematically below or
above the data points, on average).
A second aspect of the error, one that can be
estimated by NONMEM, is its typical size. Since errors may
be positive or negative, their typical size is not given by
their mean (which is zero), but by their standard deviation,
the square root of their variance. One can always simply
convert the variance into the standard deviation, and
conversely. NONMEM output gives estimates of the error
variance. With individual data this variance is denoted in
this text by 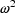 , and by OMEGA
in NONMEM input and output. The standard deviation (SD) of
the error is denoted
, and by OMEGA
in NONMEM input and output. The standard deviation (SD) of
the error is denoted 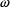 herein. The reason that OMEGA, rather than, for example,
OMEGA SQ stands for
herein. The reason that OMEGA, rather than, for example,
OMEGA SQ stands for 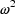 in
NONMEM input and output will be discussed in Section 3.7.
(We will see, in Chapter 4, that when the error is
symbolized by
in
NONMEM input and output will be discussed in Section 3.7.
(We will see, in Chapter 4, that when the error is
symbolized by  , not
, not
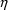 , its variance will be
denoted
, its variance will be
denoted  in this text, and
SIGMA, not OMEGA, in NONMEM input and output.) Here, the
parameter
in this text, and
SIGMA, not OMEGA, in NONMEM input and output.) Here, the
parameter  quantifies the
influence of the random effect,
quantifies the
influence of the random effect,
 on the observations,
on the observations,
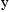 . It is therefore called a
random effects parameter.
. It is therefore called a
random effects parameter.
The symbol 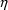 is
always used to denote a random quantity whose probability
distribution has mean zero and variance
is
always used to denote a random quantity whose probability
distribution has mean zero and variance
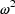 . Model (3.4) says that the
errors themselves can be so regarded, and since an
observation equals its prediction (under the structural
model) plus an error, model (3.4) is called the
Additive error model. This model is illustrated in
figure 3.2.
. Model (3.4) says that the
errors themselves can be so regarded, and since an
observation equals its prediction (under the structural
model) plus an error, model (3.4) is called the
Additive error model. This model is illustrated in
figure 3.2.
NONMEM allows an error model which can be more complicated than that of (3.4). One such more complicated, but useful model is the Constant Coefficient of Variation (CCV), or Proportional error model,
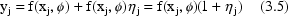
A fractional error is an error expressed as a
fraction of the corresponding prediction. The CCV model says
that a fractional error can be written as an
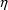 , i.e. as a random
quantity with mean zero and variance
, i.e. as a random
quantity with mean zero and variance
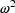 . Under this model, the
variance of an error itself is proportional to the squared
prediction, with
. Under this model, the
variance of an error itself is proportional to the squared
prediction, with  being the
proportionality factor, and so is not constant over
observations. Since, under this model, the standard
deviation of the error, and also of
being the
proportionality factor, and so is not constant over
observations. Since, under this model, the standard
deviation of the error, and also of
 , is
, is
 , and since the mean of
, and since the mean of
 is
is
 (when
(when
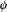 assumes its true value),
the coefficient of variation of
assumes its true value),
the coefficient of variation of
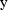 is just the constant
is just the constant
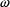 (the coefficient of
variation of a random quantity is defined as its standard
deviation divided by its mean). This is the reason the CCV
error model is so named. Also for this reason,
(the coefficient of
variation of a random quantity is defined as its standard
deviation divided by its mean). This is the reason the CCV
error model is so named. Also for this reason,
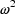 is dimensionless, in
contrast to having units equal to those of the squared
observation as with the Additive model. This error model is
illustrated in figure 3.3.
is dimensionless, in
contrast to having units equal to those of the squared
observation as with the Additive model. This error model is
illustrated in figure 3.3.
When most observations obey the CCV model but some observations may be near the lower limit of detection of an assay, a model which may be useful is one which is a combination of both the Additive and CCV error models:

Here there are two types of
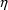 ’s,
’s,
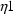 and
and
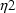 . The first has variance
. The first has variance
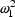 ; the second has a
possibly different variance,
; the second has a
possibly different variance,
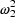 . NONMEM permits several
types of
. NONMEM permits several
types of  ’s. Under
this model, the variance of the error portion of the model
is
’s. Under
this model, the variance of the error portion of the model
is 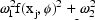 . When the prediction
is near zero, the variance is approximately constant, namely
. When the prediction
is near zero, the variance is approximately constant, namely
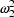 . This is the smallest
variance possible and corresponds, perhaps, to the limit of
assay precision. When the prediction is considerably greater
than zero, the variance is approximately proportional to the
squared prediction.
. This is the smallest
variance possible and corresponds, perhaps, to the limit of
assay precision. When the prediction is considerably greater
than zero, the variance is approximately proportional to the
squared prediction.
A model that has both the additive and the CCV error models as special cases, and smoothly interpolates between them in other cases is the Power Function model:
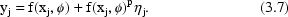
Here  is raised
to the
is raised
to the  power in the error
model, rather than the
power in the error
model, rather than the 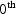 power (Additive error model; note
power (Additive error model; note
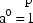 for any number,
for any number,
 ) or the first power (CCV
model). The parameter
) or the first power (CCV
model). The parameter 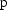 is a
fixed effects parameter, even though its role in the overall
model is to modify the variance model, not the structural
model. With NONMEM all fixed effect parameters must be
elements of the general parameter vector
is a
fixed effects parameter, even though its role in the overall
model is to modify the variance model, not the structural
model. With NONMEM all fixed effect parameters must be
elements of the general parameter vector
 . If we want the Power
Function Model to interpolate between the additive and CCV
models,
. If we want the Power
Function Model to interpolate between the additive and CCV
models,  must be
constrained to lie between 0 and 1. NONMEM allows this (see
Chapter 9). While one might be tempted to combine the Power
Function model with the Additive model, much as the CCV and
Additive model were combined above, such a combination model
can lead to identifiability difficulties, and for this
reason such a combination should be avoided.
must be
constrained to lie between 0 and 1. NONMEM allows this (see
Chapter 9). While one might be tempted to combine the Power
Function model with the Additive model, much as the CCV and
Additive model were combined above, such a combination model
can lead to identifiability difficulties, and for this
reason such a combination should be avoided.
Another more complicated error model can arise
when more than one type of measurement is made. Suppose, for
sake of illustration, that the observations are drug
concentrations, but that they are measured with two
different assays. If one assay may be more precise than the
other, then this is equivalent to saying that one assay has
a smaller 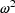 than the other.
We would like to be able to take this into account in the
analysis (i.e., not pay as much attention to the less
precise observations), and perhaps (if we have enough data)
estimate the relative precision of the assays as well. To do
this in the notation we have introduced, an independent
variable indicating which observations are obtained with
which assay is needed: we call such an independent variable
an indicator variable.
than the other.
We would like to be able to take this into account in the
analysis (i.e., not pay as much attention to the less
precise observations), and perhaps (if we have enough data)
estimate the relative precision of the assays as well. To do
this in the notation we have introduced, an independent
variable indicating which observations are obtained with
which assay is needed: we call such an independent variable
an indicator variable.
Let one of the data items (an element of
 ) be labeled
) be labeled
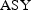 , and let
, and let
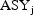 take the value 1 if the
assay used for
take the value 1 if the
assay used for 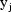 was of the
first type, and the value 0, if it was of the 2nd type. The
variable,
was of the
first type, and the value 0, if it was of the 2nd type. The
variable, 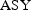 is an indicator
variable, and it allows us to write an additive type error
model, say, as
is an indicator
variable, and it allows us to write an additive type error
model, say, as
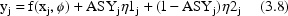
Here there are two types of
 ’s,
’s,
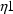 and
and
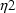 . The first applies to the
first type of assay, and has variance
. The first applies to the
first type of assay, and has variance
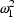 ; the second applies to
the second type of assay, and has a possibly different
variance,
; the second applies to
the second type of assay, and has a possibly different
variance, 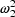 . NONMEM permits
several types of
. NONMEM permits
several types of 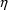 ’s.
Different types of
’s.
Different types of 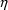 ’s can be correlated, and NONMEM can allow this.
However, this is something we would only need to consider in
the example at hand if the same blood sample were measured
by both assays. We will not emphasize this possibility in
this introductory guide. (This possibility also applies to
random variables describing unexplained interindividual
differences with population data; see Chapter 4)
’s can be correlated, and NONMEM can allow this.
However, this is something we would only need to consider in
the example at hand if the same blood sample were measured
by both assays. We will not emphasize this possibility in
this introductory guide. (This possibility also applies to
random variables describing unexplained interindividual
differences with population data; see Chapter 4)
When the assay is done by the first method,
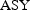 will be unity, and (3.8)
becomes
will be unity, and (3.8)
becomes

so that the variance of the error is
 . When the assay is done
by the second method,
. When the assay is done
by the second method, 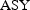 will
be zero, and (3.7) becomes
will
be zero, and (3.7) becomes

so that the variance of the error is now
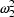 . Both
. Both
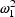 and
and
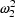 are random effect
parameters.
are random effect
parameters.
The same need for separate scales for different
measurements can arise when more than one type of
observation is made. Suppose both plasma concentrations (
 ) and urine concentrations
(
) and urine concentrations
(  ) are measured. The
structural model for
) are measured. The
structural model for 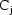 might
be (3.1), (3.3). If we assume that urine is collected
between each observation of
might
be (3.1), (3.3). If we assume that urine is collected
between each observation of
 , then the structural
model for
, then the structural
model for  , the drug
concentration in the urine collected between time
, the drug
concentration in the urine collected between time
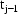 and time
and time
 might be
might be
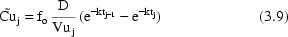
where 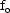 is the
fraction of drug excreted unchanged (a parameter), and
is the
fraction of drug excreted unchanged (a parameter), and
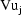 is the urine volume
collected between time
is the urine volume
collected between time 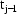 and
and
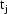 (a data item)†.
(a data item)†.
----------

Assuming again, for sake of the example, that we
want to use an additive type error model for the
observations, the problem is that urine concentrations can
be orders of magnitude larger than plasma concentrations, so
that, while an additive error model might be appropriate for
either type of observation alone, the two types of
observations must have different typical error magnitudes;
i.e., different variances (
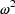 ’s).
’s).
An indicator variable can again be used. Let the
indicator variable 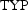 be
unity if the
be
unity if the 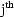 observation
is a
observation
is a  , and 0 if it is a
, and 0 if it is a
 . We now need to use it
for both the structural and error models, so
that:
. We now need to use it
for both the structural and error models, so
that:
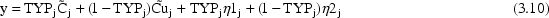
A little thought shows that the indicator
variable selects the correct prediction (
 or
or
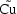 ) and the correct error
term for each observation (
) and the correct error
term for each observation (
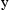 ).
).
Of course, there could be three types of assays,
or more, and similarly, more than two types of observations.
One usually needs one less indicator variable than types of
things to be distinguished. So, if there were three assays,
one would define 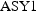 and
and
 .
.
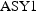 would be 1 if the assay
were of the first type, and zero otherwise;
would be 1 if the assay
were of the first type, and zero otherwise;
 would be 1 if the assay
were of the second type, and zero otherwise. The error model
for the data would require three types of
would be 1 if the assay
were of the second type, and zero otherwise. The error model
for the data would require three types of
 ’s,
’s,
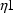 ,
,
 , and
, and
 .
.
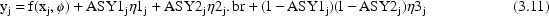
Equation (3.11) results in the following:

We have just seen examples of more complicated error models than the simple Additive model. We here give a mathematical form for the most general mixed effects model that is considered within the scope of this document:
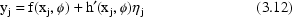
where 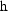 is a vector
valued function of
is a vector
valued function of  and
parameters
and
parameters 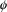 (where the
latter is interpreted broadly to contain parameters such as
(where the
latter is interpreted broadly to contain parameters such as
 of (3.7)), and
of (3.7)), and
 is a vector of different
different
is a vector of different
different 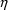 types. The
notation
types. The
notation  denotes vector
transpose. When there is more than one
denotes vector
transpose. When there is more than one
 type, there will be
several
type, there will be
several 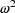 ’s, one for
each type. The collection of these is denoted
’s, one for
each type. The collection of these is denoted
 and is labeled OMEGA in
NONMEM input and output. This collection is regarded as a
diagonal matrix (diagonal for now; but see Chapter 4),
rather than as a vector. We will use the symbol
and is labeled OMEGA in
NONMEM input and output. This collection is regarded as a
diagonal matrix (diagonal for now; but see Chapter 4),
rather than as a vector. We will use the symbol
 and
and
 interchangeably in this
text to denote the (diagonal) element of this matrix found
in position
interchangeably in this
text to denote the (diagonal) element of this matrix found
in position 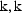 .
.